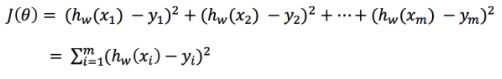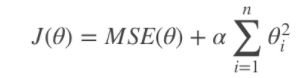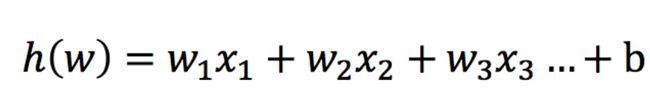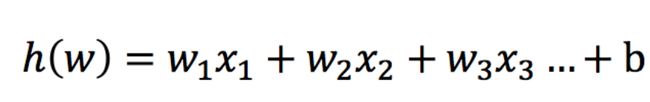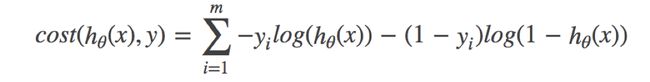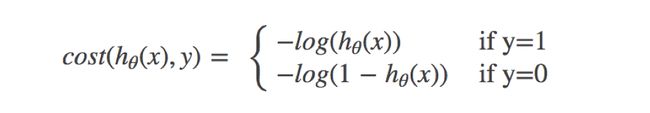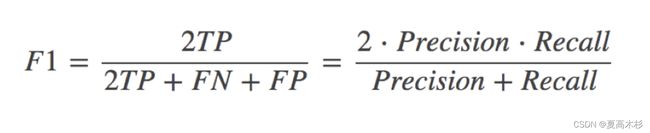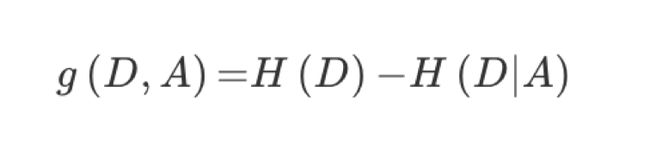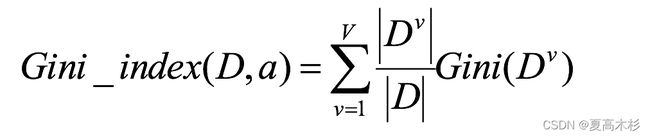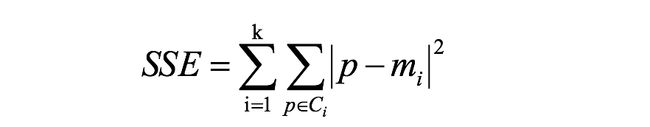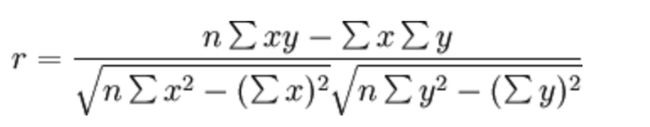机器学习python的api笔记

已经使用的软件
numpy
pandas
Matplotlib
tables
jutyper
sklearn

1.K近邻算法

加入Scikit-learn工具

安装scikit-learn需要Numpy, Scipy等库
包含内容

分类、聚类、回归
特征工程
模型选择、调优

数据集api介绍

• sklearn.datasets
  • 加载获取流行数据集
  • datasets.load_*()
    • 获取小规模数据集，数据包含在datasets里
  • datasets.fetch_*(data_home=None)
    • 获取大规模数据集，需要从网络上下载，函数的第一个参数是data_home，表示数据集下载的目录,默认是~/scikit_learn_data/

小数据集

sklearn.datasets.load_iris()

加载并返回鸢尾花数据集

大数据集

• sklearn.datasets.fetch_20newsgroups(data_home=None,subset=‘train’)
  • subset：‘train’或者’test’，‘all’，可选，选择要加载的数据集。
  • 训练集的“训练”，测试集的“测试”，两者的“全部”

数据集返回值介绍

• load和fetch返回的数据类datasets.base.Bunch(字典格式)
  • data：特征数据数组，是 [n_samples * n_features] 的二维 numpy.ndarray 数组
  • target：标签数组，是 n_samples 的一维 numpy.ndarray 数组
  • DESCR：数据描述
  • feature_names：特征名,新闻数据，手写数字、回归数据集没有
  • target_names：标签名

特征值处理api

归一化
注意最大值最小值是变化的，另外，最大值与最小值非常容易受异常点影响，所以这种方法鲁棒性较差，只适合传统精确小数据场景。

• sklearn.preprocessing.MinMaxScaler (feature_range=(0,1)… )
  • MinMaxScalar.fit_transform(X)
    • X:numpy array格式的数据[n_samples,n_features]
  • 返回值：转换后的形状相同的array
    标准化
• sklearn.preprocessing.StandardScaler( )
  • 处理之后每列来说所有数据都聚集在均值0附近标准差差为1
  • StandardScaler.fit_transform(X)
    • X:numpy array格式的数据[n_samples,n_features]
  • 返回值：转换后的形状相同的array

# coding:utf-8

from sklearn.preprocessing import MinMaxScaler, StandardScaler
import pandas as pd

data = pd.read_csv("./data/dating.txt")
print(data)

# # 1.归一化
# # 1.1 实例化一个转换器
transfer = MinMaxScaler(feature_range=(0, 10))
# # 1.2 调用fit_transfrom方法
minmax_data = transfer.fit_transform(data[['milage', 'Liters', 'Consumtime']])
print("经过归一化处理之后的数据为:\n", minmax_data)


# 2.标准化
# 2.1 实例化一个转换器
transfer = StandardScaler()
# 2.2 调用fit_transfrom方法
minmax_data = transfer.fit_transform(data[['milage', 'Liters', 'Consumtime']])
print("经过标准化处理之后的数据为:\n", minmax_data)

API

• sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)
  • n_neighbors：int,可选（默认= 5），k_neighbors查询默认使用的邻居数。 新样例进入，选五个与其最近的看它的类别，五个里面属于哪个的最多，新样例就归类于哪个类别
  • algorithm{‘auto’，‘ball_tree’，‘kd_tree’，‘brute’}
    • 快速k近邻搜索算法，默认参数为auto，可以理解为算法自己决定合适的搜索算法。除此之外，用户也可以自己指定搜索算法ball_tree、kd_tree、brute方法进行搜索，
      • brute是蛮力搜索，也就是线性扫描，当训练集很大时，计算非常耗时。
      • kd_tree，构造kd树存储数据以便对其进行快速检索的树形数据结构，kd树也就是数据结构中的二叉树。以中值切分构造的树，每个结点是一个超矩形，在维数小于20时效率高。
      • ball tree是为了克服kd树高纬失效而发明的，其构造过程是以质心C和半径r分割样本空间，每个节点是一个超球体。

example:

# coding:utf-8

from sklearn.neighbors import KNeighborsClassifier

# 获取数据
x = [[1], [2], [0], [0]]
y = [1, 1, 0, 0]

# 机器学习
# 1.实例化一个训练模型
estimator = KNeighborsClassifier(n_neighbors=2)
# 2.调用fit方法进行训练
estimator.fit(x, y)

# 预测其他值
ret = estimator.predict([[24]])
print(f'输出结果是{ret}')

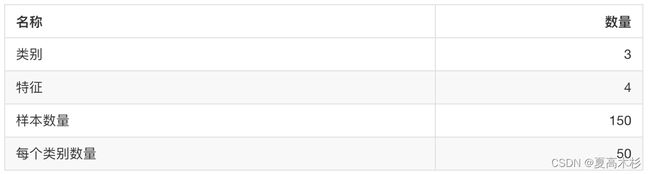
案例一鸢尾花种类预测–数据集介绍

# coding:utf-8

import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import load_iris, fetch_20newsgroups
from sklearn.model_selection import train_test_split

# 1.数据集获取
# 1.1 小数据集获取
iris = load_iris()
# print(f'第一次展示数据{iris}');

# 1.2 大数据集获取
news = fetch_20newsgroups()
# print(news)

# 2.数据集属性描述
# print("数据集中特征值是:\n", iris.data)
# print("数据集中目标值是:\n", iris["target"])
# print("数据集中特征值名字是:\n", iris.feature_names)
# print("数据集中目标值名字是:\n", iris.target_names)
# print("数据集的描述:\n", iris.DESCR)

# 3.数据可视化
# 3.1 数据类型转换,把数据用DataFrame存储
iris_data = pd.DataFrame(data=iris.data, columns=['Sepal_Length', 'Sepal_Width', 'Petal_Length', 'Petal_Width'])
iris_data["target"] = iris.target


# print(iris_data)


def iris_plot(data, col1, col2):
    sns.lmplot(x=col1, y=col2, data=data, hue="target", fit_reg=False)
    plt.title("鸢尾花数据展示")
    plt.xlabel(col1)
    plt.ylabel(col2)
    plt.show()


# iris_plot(iris_data, "Sepal_Length", 'Petal_Width')
# iris_plot(iris_data, 'Sepal_Width', 'Petal_Length')


# 4.数据集的划分
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=2)
# print("训练集的特征值是:\n", x_train)
# print("训练集的目标值是:\n", y_train)
# print("测试集的特征值是:\n", x_test)
# print("测试集的目标值是:\n", y_test)


# print("训练集的目标值形状:\n", y_train.shape)
# print("测试集的目标值形状:\n", y_test.shape)


x_train1, x_test1, y_train1, y_test1 = train_test_split(iris.data, iris.target, test_size=0.2, random_state=22)
x_train2, x_test2, y_train2, y_test2 = train_test_split(iris.data, iris.target, test_size=0.2, random_state=22)
print("测试集的目标值是:\n", y_test1)
print("测试集的目标值是:\n", y_test2)

用到的工具

seaborn介绍

• Seaborn 是基于 Matplotlib 核心库进行了更高级的 API 封装，可以让你轻松地画出更漂亮的图形。而 Seaborn 的漂亮主要体现在配色更加舒服、以及图形元素的样式更加细腻。
• 安装 pip3 install seaborn
• seaborn.lmplot() 是一个非常有用的方法，它会在绘制二维散点图时，自动完成回归拟合
  • sns.lmplot() 里的 x, y 分别代表横纵坐标的列名,
  • data= 是关联到数据集,
  • hue=*代表按照 species即花的类别分类显示,
  • fit_reg=是否进行线性拟合。

案例2-鸢尾花种类预测—流程实现

# coding:utf-8
"""
1.获取数据集
2.数据基本处理
3.特征工程
4.机器学习(模型训练)
5.模型评估
"""

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier

# 1.获取数据集
iris = load_iris()

# 2.数据基本处理
# 2.1 数据分割
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22, test_size=0.2)

# 3.特征工程
# 3.1 实例化一个转换器
transfer = StandardScaler()
# 3.2 调用fit_transform方法
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)

# 4.机器学习(模型训练)
# 4.1 实例化一个估计器
estimator = KNeighborsClassifier(n_neighbors=5)
# 4.2 模型训练
estimator.fit(x_train, y_train)

# 5.模型评估
# 5.1 输出预测值
y_pre = estimator.predict(x_test)
print("预测值是:\n", y_pre)
print("预测值和真实值对比:\n", y_pre == y_test)

# 5.2 输出准确率
ret = estimator.score(x_test, y_test)
print("准确率是:\n", ret)

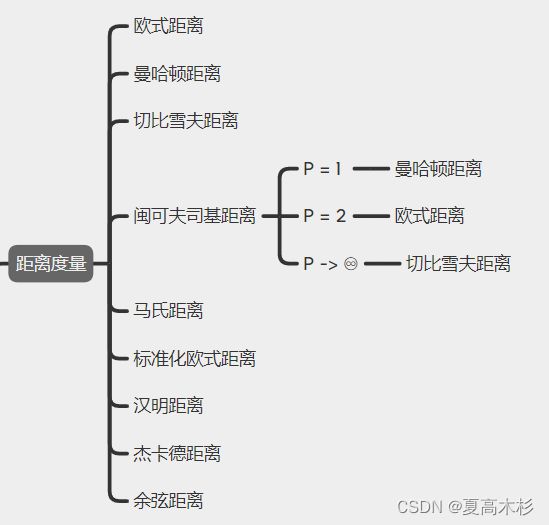
距离度量

kd树

构造方法

（1）构造根结点，使根结点对应于K维空间中包含所有实例点的超矩形区域；

（2）通过递归的方法，不断地对k维空间进行切分，生成子结点。在超矩形区域上选择一个坐标轴和在此坐标轴上的一个切分点，确定一个超平面，这个超平面通过选定的切分点并垂直于选定的坐标轴，将当前超矩形区域切分为左右两个子区域（子结点）；这时，实例被分到两个子区域。

（3）上述过程直到子区域内没有实例时终止（终止时的结点为叶结点）。在此过程中，将实例保存在相应的结点上。

（4）通常，循环的选择坐标轴对空间切分，选择训练实例点在坐标轴上的中位数为切分点，这样得到的kd树是平衡的（平衡二叉树：它是一棵空树，或其左子树和右子树的深度之差的绝对值不超过1，且它的左子树和右子树都是平衡二叉树）。

KD树中每个节点是一个向量，和二叉树按照数的大小划分不同的是，KD树每层需要选定向量中的某一维，然后根据这一维按左小右大的方式划分数据。在构建KD树时，关键需要解决2个问题：

（1）选择向量的哪一维进行划分；

（2）如何划分数据；

第一个问题简单的解决方法可以是随机选择某一维或按顺序选择，但是更好的方法应该是在数据比较分散的那一维进行划分（分散的程度可以根据方差来衡量）。好的划分方法可以使构建的树比较平衡，可以每次选择中位数来进行划分，这样问题2也得到了解决。

kd树点查找方法

首先通过二叉树搜索（比较待查询节点和分裂节点的分裂维的值，小于等于就进入左子树分支，大于就进入右子树分支直到叶子结点），顺着“搜索路径”很快能找到最近邻的近似点，也就是与待查询点处于同一个子空间的叶子结点；

然后再回溯搜索路径，并判断搜索路径上的结点的其他子结点空间中是否可能有距离查询点更近的数据点，如果有可能，则需要跳到其他子结点空间中去搜索（将其他子结点加入到搜索路径）。

重复这个过程直到搜索路径为空。

算法总结

优点：

• 简单有效
• 重新训练的代价低
• 适合类域交叉样本(样本之间重叠较多)
  • KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。
• 适合大样本自动分类
  • 该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分。

缺点：

• 惰性学习
  • KNN算法是懒散学习方法（lazy learning,基本上不学习），一些积极学习的算法要快很多
• 类别评分不是规格化
  • 不像一些通过概率评分的分类
• 输出可解释性不强
  • 例如决策树的输出可解释性就较强
• 对不均衡的样本不擅长
  • 当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。该算法只计算“最近的”邻居样本，某一类的样本数量很大，那么或者这类样本并不接近目标样本，或者这类样本很靠近目标样本。无论怎样，数量并不能影响运行结果。可以采用权值的方法（和该样本距离小的邻居权值大）来改进。
• 计算量较大
  • 目前常用的解决方法是事先对已知样本点进行剪辑，事先去除对分类作用不大的样本。

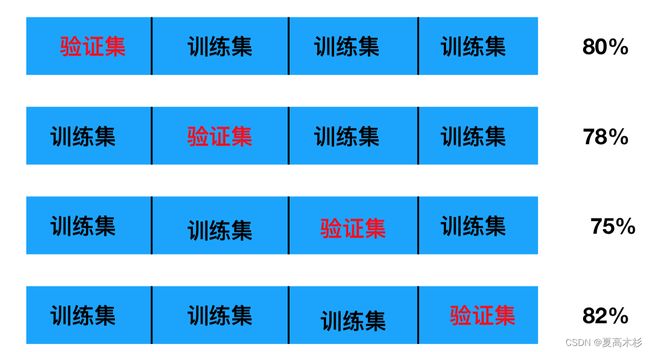
交叉验证(cross validation)

数据分训练集与测试集

训练集：训练集+验证集
测试集：测试集

交叉验证目的：为了让被评估的模型更加准确可信
并不一定可以提高模型准确率

网格搜索(Grid Search)

通常情况下，有很多参数是需要手动指定的（如k-近邻算法中的K值），这种叫超参数。但是手动过程繁杂，所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。

api

• sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)
  • 对估计器的指定参数值进行详尽搜索
  • estimator：估计器对象
  • param_grid：估计器参数(dict){“n_neighbors”:[1,3,5]}
  • cv：指定几折交叉验证
  • n_job：几核跑代码 -1为满负荷
  • 方法
    • fit：输入训练数据
    • score：准确率
    • 结果分析：
      • bestscore__:在交叉验证中验证的最好结果
      • bestestimator：最好的参数模型
      • cvresults:每次交叉验证后的验证集准确率结果和训练集准确率结果

# coding:utf-8
"""
1.获取数据集
2.数据基本处理
3.特征工程
4.机器学习(模型训练)
5.模型评估
"""

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier

# 1.获取数据集
iris = load_iris()

# 2.数据基本处理
# 2.1 数据分割
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2)

# 3.特征工程
# 3.1 实例化一个转换器
transfer = StandardScaler()
# 3.2 调用fit_transform方法
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)


# 4.机器学习(模型训练)
# 4.1 实例化一个估计器
estimator = KNeighborsClassifier()

# 4.2 调用交叉验证网格搜索模型
param_grid = {"n_neighbors": [1, 3, 5, 7, 9]}
estimator = GridSearchCV(estimator, param_grid=param_grid, cv=10, n_jobs=-1)

# 4.3 模型训练
estimator.fit(x_train, y_train)

# 5.模型评估
# 5.1 输出预测值
y_pre = estimator.predict(x_test)
print("预测值是:\n", y_pre)
print("预测值和真实值对比:\n", y_pre == y_test)

# 5.2 输出准确率
ret = estimator.score(x_test, y_test)
print("准确率是:\n", ret)

# 5.3 其他评价指标
print("最好的模型：\n", estimator.best_estimator_)
print("最好的结果:\n", estimator.best_score_)
print("整体模型结果:\n", estimator.cv_results_)

facebook案例预测

import pandas as pd
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
# 1、获取数据集
facebook = pd.read_csv("./data/FBlocation/train.csv")
# 2.基本数据处理
# 2.1 缩小数据范围
facebook_data = facebook.query("x>2.0 & x<2.5 & y>2.0 & y<2.5")
# 2.2 选择时间特征
time = pd.to_datetime(facebook_data["time"], unit="s")
time = pd.DatetimeIndex(time)
facebook_data["day"] = time.day
facebook_data["hour"] = time.hour
facebook_data["weekday"] = time.weekday
# 2.3 去掉签到较少的地方
place_count = facebook_data.groupby("place_id").count()
place_count = place_count[place_count["row_id"]>3]
facebook_data = facebook_data[facebook_data["place_id"].isin(place_count.index)] # 表示包含在此集中
# 2.4 确定特征值和目标值
x = facebook_data[["x", "y", "accuracy", "day", "hour", "weekday"]]
y = facebook_data["place_id"]
# 2.5 分割数据集
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)

# 3.特征工程--特征预处理(标准化)
# 3.1 实例化一个转换器
transfer = StandardScaler()
# 3.2 调用fit_transform
x_train = transfer.fit_transform(x_train)
# x_test = transfer.transform(x_test) # 也可以直接调用训练好的转换器，因为差距不大，直接调用可以节省时间
x_test = transfer.fit_transform(x_test)

# 4.机器学习--knn+cv
# 4.1 实例化一个估计器
estimator = KNeighborsClassifier()
# 4.2 调用gridsearchCV
param_grid = {"n_neighbors": [1, 3, 5, 7, 9]}
estimator = GridSearchCV(estimator, param_grid=param_grid, cv=5)
# 4.3 模型训练
estimator.fit(x_train, y_train)

# 5.模型评估
# 5.1 基本评估方式
score = estimator.score(x_test, y_test)
print("最后预测的准确率为:\n", score)

y_predict = estimator.predict(x_test)
print("最后的预测值为:\n", y_predict)
print("预测值和真实值的对比情况:\n", y_predict == y_test)

# 5.2 使用交叉验证后的评估方式
print("在交叉验证中验证的最好结果:\n", estimator.best_score_)
print("最好的参数模型:\n", estimator.best_estimator_)
print("每次交叉验证后的验证集准确率结果和训练集准确率结果:\n",estimator.cv_results_)

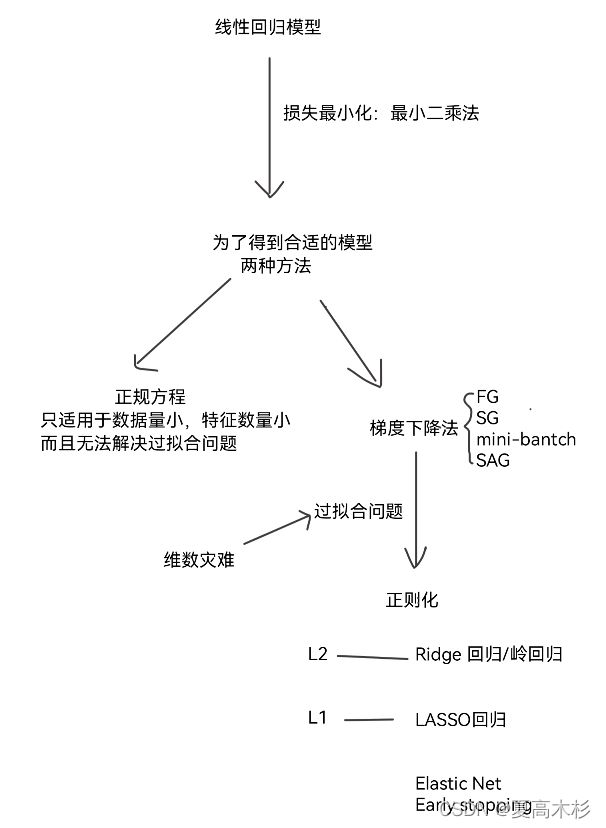
2. 线性回归

1. 定义
   利用回归方程(Linear regression)(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式
   特点：只有一个自变量的情况称为单变量回归，多于一个自变量情况的叫做多元回归

2. 表示方式:
   h(w) = w1x1 + w2x2 + w3x3 + … + b
   = W转置x + b

3. 分类
   线性关系
   非线性关系 如果是非线性关系，那么回归方程可以理解为：w1x1+w2x2²+w3x3^2

思路：

线性回归的损失和优化

损失

最小二乘法

优化

正规方程 与 梯度下降法

正规方程 – 一蹴而就

利用矩阵的逆,转置进行一步求解
只是适合样本和特征比较少的情况

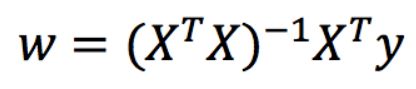
理解：X为特征值矩阵，y为目标值矩阵。直接求到最好的结果

缺点：当特征过多过复杂时，求解速度太慢并且得不到结果

梯度下降法(Gradient Descent) – 循序渐进

• 举例:
  • 山 – 可微分的函数
  • 山底 – 函数的最小值
• 梯度的概念
  • 单变量 – 切线
  • 多变量 – 向量
• 梯度下降法中关注的两个参数
  • α – 就是步长
    • 步长太小 – 下山太慢
    • 步长太大 – 容易跳过极小值点(*****)
  • 为什么梯度要加一个负号
    • 梯度方向是上升最快方向,负号就是下降最快方向

梯度下降法介绍
1 全梯度下降算法（FG）:在进行计算的时候,计算所有样本的误差平均值,作为我的目标函数
2 随机梯度下降算法（SG）:每次只选择一个样本进行考核
3 小批量梯度下降算法（mini-bantch）:选择一部分样本进行考核 （用的最多）
4 随机平均梯度下降算法（SAG）:会给每个样本都维持一个平均值,后期计算的时候,参考这个平均值
拓展（深度学习再学）
动量法、Nesterov加速梯度下降法、Adagrad、Adadelta、RMSProp、Adam

• 梯度下降法和正规方程对比:

  梯度下降	正规方程
  需要选择学习率	不需要
  需要迭代求解	一次运算得出
  特征数量较大可以使用	需要计算方程，时间复杂度高O(n3)

选择：

• 小规模数据：
  • LinearRegression(不能解决拟合问题)
  • 岭回归
• 大规模数据：
  • SGDRegressor

过拟合的解决-正则化

• 过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合， 但是在测试数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。(模型过于复杂)
• 欠拟合：一个假设在训练数据上不能获得更好的拟合，并且在测试数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。(模型过于简单)

解决过拟合有很多方法，线性回归选择正则化。但是对于其他机器学习算法如分类算法来说也会出现这样的问题，除了一些算法本身作用之外（决策树、神经网络），我们更多的也是去自己做特征选择，包括之前说的删除、合并一些特征

正则化

正则化：在学习的时候，数据提供的特征有些影响模型复杂度或者这个特征的数据点异常较多，所以算法在学习的时候尽量减少这个特征的影响（甚至删除某个特征的影响）
注：调整时候，算法并不知道某个特征影响，而是去调整参数得出优化的结果

类别：

• L2正则化
  • 作用：可以使得其中一些W的都很小，都接近于0，削弱某个特征的影响
  • 优点：越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象
  • Ridge回归
• L1正则化
  • 作用：可以使得其中一些W的值直接为0，删除这个特征的影响
  • LASSO回归

维数灾难与过拟合
维数灾难：随着维度(特征数量)的增加，分类器的性能却下降了
高维空间训练形成的线性分类器，相当于在低维空间的一个复杂的非线性分类器
训练集的维度越多，过度拟合的风险就越大。
所需的训练实例数量随着使用的维度数量呈指数增长。

正则化线性模型

1. Ridge Regression 岭回归

就是把系数添加平方项，然后限制系数值的大小

α值越小，系数值越大，α越大，系数值越小
2. Lasso 回归
对系数值进行绝对值处理

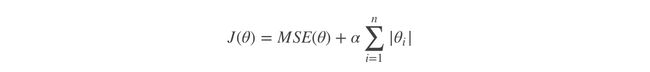
由于绝对值在顶点处不可导，所以进行计算的过程中产生很多0，最后得到结果为：稀疏矩阵
3. Elastic Net 弹性网络
是前两个内容的综合
设置了一个r,如果r=0–岭回归；r=1–Lasso回归

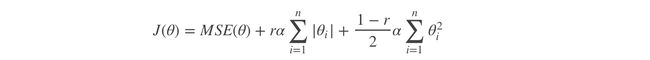
4. Early stopping
   通过限制错误率的阈值，进行停止

选择：

• 常用：岭回归
• 假设只有少部分特征是有用的：
  • 弹性网络
  • Lasso
  • 一般来说，弹性网络的使用更为广泛。因为在特征维度高于训练样本数，或者特征是强相关的情况下，Lasso回归的表现不太稳定。

线性回归性能评估

均方误差(Mean Squared Error)MSE)评价机制：

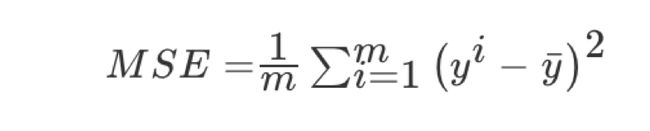
注：yi为预测值，¯y为真实值

• sklearn.metrics.mean_squared_error(y_true, y_pred)
  • 均方误差回归损失
  • y_true:真实值
  • y_pred:预测值
  • return:浮点数结果

api

• sklearn.linear_model.LinearRegression(fit_intercept=True)

  • 通过正规方程优化
  • fit_intercept：是否计算偏置
  • LinearRegression.coef_：回归系数
  • LinearRegression.intercept_：偏置

• sklearn.linear_model.SGDRegressor(loss=“squared_loss”, fit_intercept=True, learning_rate =‘invscaling’, eta0=0.01)

  • SGDRegressor类实现了随机梯度下降学习，它支持不同的loss函数和正则化惩罚项来拟合线性回归模型。
  • loss:损失类型
    • loss=”squared_loss”: 普通最小二乘法
  • fit_intercept：是否计算偏置
  • learning_rate : string, optional
    • 学习率填充
    • ‘constant’: eta = eta0
    • ‘optimal’: eta = 1.0 / (alpha * (t + t0)) [default]
    • ‘invscaling’: eta = eta0 / pow(t, power_t)
      • power_t=0.25:存在父类当中
    • 对于一个常数值的学习率来说，可以使用learning_rate=’constant’ ，并使用eta0来指定学习率。
  • SGDRegressor.coef_：回归系数
  • SGDRegressor.intercept_：偏置

岭回归api

• sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver=“auto”, normalize=False)
  • 具有l2正则化的线性回归
  • alpha:正则化力度，也叫 λ
    • λ取值：0~1 1~10
  • solver:会根据数据自动选择优化方法
    • sag(优先):如果数据集、特征都比较大，选择该随机梯度下降优化
  • normalize:数据是否进行标准化
    • normalize=False:可以在fit之前调用preprocessing.StandardScaler标准化数据
  • Ridge.coef_:回归权重
  • Ridge.intercept_:回归偏置

Ridge方法相当于SGDRegressor(penalty=‘l2’, loss=“squared_loss”),只不过SGDRegressor实现了一个普通的随机梯度下降学习，推荐使用Ridge(实现了SAG)

• sklearn.linear_model.RidgeCV(_BaseRidgeCV, RegressorMixin)

  • 具有l2正则化的线性回归，可以进行交叉验证
  • coef_:回归系数

• 正则化力度越大，权重系数会越小

• 正则化力度越小，权重系数会越大

实例

# coding:utf-8

"""
1.获取数据
2.数据基本处理
2.1 数据集划分
3.特征工程 --标准化
4.机器学习(线性回归)
5.模型评估
"""

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge, RidgeCV
from sklearn.metrics import mean_squared_error


def linear_model1():
    """
    正规方程
    :return: None
    """
    # 1.获取数据
    boston = load_boston()

    # 2.数据基本处理
    # 2.1 数据集划分
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.2)

    # 3.特征工程 --标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)

    # 4.机器学习(线性回归)
    estimator = LinearRegression()
    estimator.fit(x_train, y_train)
    print("这个模型的偏置是:\n", estimator.intercept_)

    # 5.模型评估
    # 5.1 预测值和准确率
    y_pre = estimator.predict(x_test)
    print("预测值是:\n", y_pre)

    score = estimator.score(x_test, y_test)
    print("准确率是:\n", score)

    # 5.2 均方误差
    ret = mean_squared_error(y_test, y_pre)
    print("均方误差是:\n", ret)


def linear_model2():
    """
    梯度下降法
    :return: None
    """
    # 1.获取数据
    boston = load_boston()

    # 2.数据基本处理
    # 2.1 数据集划分
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.2)

    # 3.特征工程 --标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)

    # 4.机器学习(线性回归)
    estimator = SGDRegressor(max_iter=1000, learning_rate="constant", eta0=0.001)

    estimator.fit(x_train, y_train)
    print("这个模型的偏置是:\n", estimator.intercept_)

    # 5.模型评估
    # 5.1 预测值和准确率
    y_pre = estimator.predict(x_test)
    print("预测值是:\n", y_pre)

    score = estimator.score(x_test, y_test)
    print("准确率是:\n", score)

    # 5.2 均方误差
    ret = mean_squared_error(y_test, y_pre)
    print("均方误差是:\n", ret)


def linear_model3():
    """
    岭回归
    :return: None
    """
    # 1.获取数据
    boston = load_boston()

    # 2.数据基本处理
    # 2.1 数据集划分
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.2)

    # 3.特征工程 --标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)

    # 4.机器学习(线性回归)
    # estimator = Ridge()
    estimator = RidgeCV(alphas=(0.001, 0.1, 1, 10, 100))

    estimator.fit(x_train, y_train)
    print("这个模型的偏置是:\n", estimator.intercept_)

    # 5.模型评估
    # 5.1 预测值和准确率
    y_pre = estimator.predict(x_test)
    print("预测值是:\n", y_pre)

    score = estimator.score(x_test, y_test)
    print("准确率是:\n", score)

    # 5.2 均方误差
    ret = mean_squared_error(y_test, y_pre)
    print("均方误差是:\n", ret)


if __name__ == '__main__':
    linear_model1()
    linear_model2()
    linear_model3()

模型的保存和加载api

• from sklearn.externals import joblib
  • 保存：joblib.dump(estimator, ‘test.pkl’)
  • 加载：estimator = joblib.load(‘test.pkl’)

def load_dump_demo():
    """
    线性回归:岭回归
    :return:
    """
    # 1.获取数据
    data = load_boston()

    # 2.数据集划分
    x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)

    # 3.特征工程-标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)

    # 4.机器学习-线性回归(岭回归)
    # # 4.1 模型训练
    # estimator = Ridge(alpha=1)
    # estimator.fit(x_train, y_train)
    #
    # # 4.2 模型保存
    # joblib.dump(estimator, "./data/test.pkl")

    # 4.3 模型加载
    estimator = joblib.load("./data/test.pkl")

    # 5.模型评估
    # 5.1 获取系数等值
    y_predict = estimator.predict(x_test)
    print("预测值为:\n", y_predict)
    print("模型中的系数为:\n", estimator.coef_)
    print("模型中的偏置为:\n", estimator.intercept_)

    # 5.2 评价
    # 均方误差
    error = mean_squared_error(y_test, y_predict)
    print("误差为:\n", error)

3. 逻辑回归

解决的是一个二分类问题
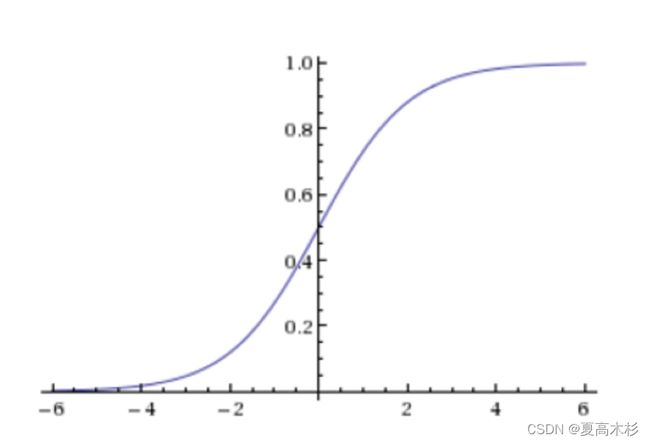
逻辑回归的输入是线性回归的输出

原理

1. 输入：
   
   线性回归的输出

2. 激活函数
   sigmoid函数
   

    把整体的值映射到[0,1]
    再设置一个阈值，进行分类判断
   

3. 损失
   对数似然损失
   
   借助了log思想，进行完成
   真实值等于0，等于1两种情况进行划分
   分开类别
   

4. 优化
   提升原本属于1类别的概率，降低原本是0类别的概率。

api

• sklearn.linear_model.LogisticRegression(solver=‘liblinear’, penalty=‘l2’, C = 1.0)
  • solver可选参数:{‘liblinear’, ‘sag’, ‘saga’,‘newton-cg’, ‘lbfgs’}，
    • 默认: ‘liblinear’；用于优化问题的算法。
    • 对于小数据集来说，“liblinear”是个不错的选择，而“sag”和’saga’对于大型数据集会更快。
    • 对于多类问题，只有’newton-cg’， ‘sag’， 'saga’和’lbfgs’可以处理多项损失;“liblinear”仅限于“one-versus-rest”分类。
  • penalty：正则化的种类
  • C：正则化力度

默认将类别数量少的当做正例

LogisticRegression方法相当于 SGDClassifier(loss=“log”, penalty=" "),SGDClassifier实现了一个普通的随机梯度下降学习。而使用LogisticRegression(实现了SAG)

在很多分类场景当中我们不一定只关注预测的准确率。比如以这个癌症举例子！！！我们并不关注预测的准确率，而是关注在所有的样本当中，癌症患者有没有被全部预测（检测）出来。

分类评估方法

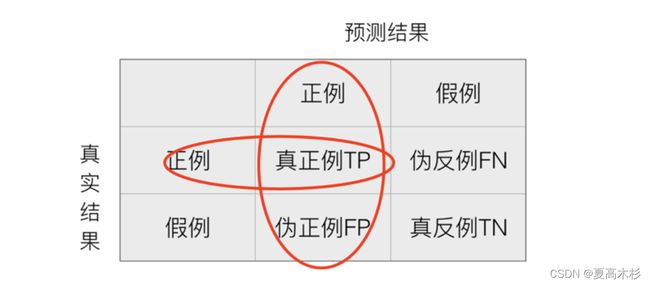
混淆矩阵

在分类任务下，预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合，构成混淆矩阵(适用于多分类)

• 精确率(Precision)：预测结果为正例样本中真实为正例的比例
  

• 召回率(Recall)：真实为正例的样本中预测结果为正例的比例（查得全，对正样本的区分能力）
  

• F1-score
  还有其他的评估标准，F1-score，反映了模型的稳健型
  

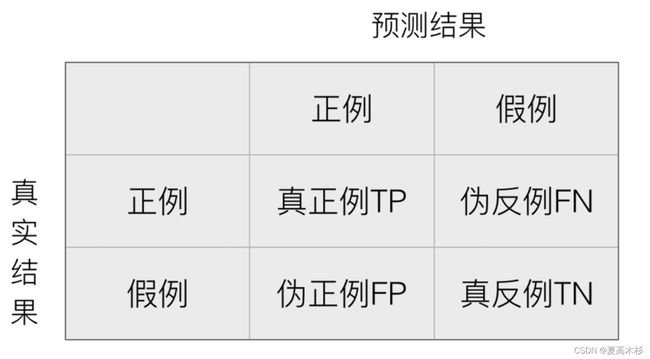
api

• sklearn.metrics.classification_report(y_true, y_pred, labels=[], target_names=None )
  • y_true：真实目标值
  • y_pred：估计器预测目标值
  • labels:指定类别对应的数字
  • target_names：目标类别名称
  • return：每个类别精确率与召回率

ROC曲线与AUC指标

• TPR = TP / (TP + FN)
  • 所有真实类别为1的样本中，预测类别为1的比例
• FPR = FP / (FP + TN)
  • 所有真实类别为0的样本中，预测类别为1的比例

ROC曲线
ROC曲线的横轴就是FPRate，纵轴就是TPRate，当二者相等时，表示的意义则是：对于不论真实类别是1还是0的样本，分类器预测为1的概率是相等的，此时AUC为0.5(可以理解为面积)

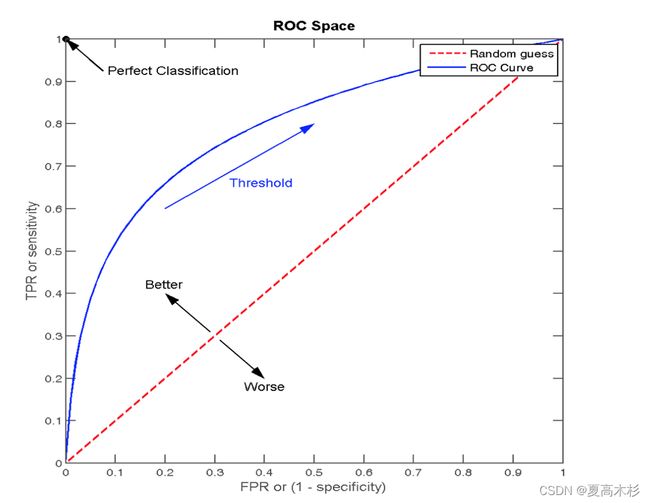
AUC指标

• AUC的概率意义是随机取一对正负样本，正样本得分大于负样本的概率
• AUC的最小值为0.5，最大值为1，取值越高越好
• AUC=1，完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。
• 0.5

最终AUC的范围在[0.5, 1]之间，并且越接近1越好
AUC只能用来评价二分类
AUC非常适合评价样本不平衡中的分类器性能

api

• from sklearn.metrics import roc_auc_score
  • sklearn.metrics.roc_auc_score(y_true, y_score)
    • 计算ROC曲线面积，即AUC值
    • y_true：每个样本的真实类别，必须为0(反例),1(正例)标记
    • y_score：预测得分，可以是正类的估计概率、置信值或者分类器方法的返回值

案例

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
from sklearn.metrics import roc_auc_score

import ssl
ssl._create_default_https_context = ssl._create_unverified_context

# 1.获取数据
names = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape',
                   'Marginal Adhesion', 'Single Epithelial Cell Size', 'Bare Nuclei', 'Bland Chromatin',
                   'Normal Nucleoli', 'Mitoses', 'Class']

data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data",
                  names=names)
data.head()

# 2.基本数据处理
# 2.1 缺失值处理
data = data.replace(to_replace="?", value=np.NaN)
data = data.dropna()
# 2.2 确定特征值,目标值
x = data.iloc[:, 1:10]
x.head()
y = data["Class"]
y.head()
# 2.3 分割数据
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)


# 3.特征工程(标准化)
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 4.机器学习(逻辑回归)
estimator = LogisticRegression()
estimator.fit(x_train, y_train)

# 5.模型评估
# 5.1 基本评估
y_pre = estimator.predict(x_test)
print("预测值是：\n", y_pre)

score = estimator.score(x_test, y_test)
print("准确率是：\n", score)

# 5.2 其他评估
ret = classification_report(y_test, y_pre, labels=(2,4), target_names=("良性", "恶性"))
print(ret)

# 不平衡二分类问题评估方法
y_test = np.where(y_test>3, 1, 0)

roc_auc_score(y_true=y_test, y_score=y_pre)

4. 决策树

决策树：是一种树形结构，其中每个内部节点表示一个属性上的判断，每个分支代表一个判断结果的输出，最后每个叶节点代表一种分类结果，本质是一颗由多个判断节点组成的树。

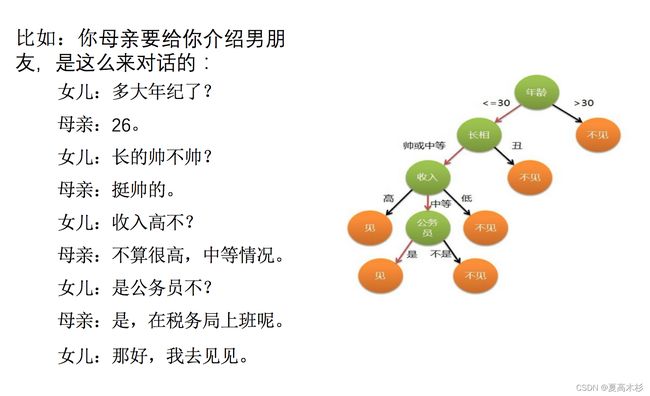
1.熵
用于衡量一个对象的有序程度
系统越有序，熵值越低；系统越混乱或者分散，熵值越高。
2.信息熵
1.从信息的完整性上进行的描述:
当系统的有序状态一致时，数据越集中的地方熵值越小，数据越分散的地方熵值越大。
2.从信息的有序性上进行的描述:
当数据量一致时，系统越有序，熵值越低；系统越混乱或者分散，熵值越高。
3.把信息转换成熵值
-plogp

划分依据

信息增益

信息增益 = entroy(前) - entroy(后)

信息增益率

增益率：增益比率度量是用前面的增益度量Gain(S，A)和所分离信息度量SplitInformation(如上例的性别，活跃度等)的比值来共同定义的。

基尼指数

基尼值Gini（D）：从数据集D中随机抽取两个样本，其类别标记不一致的概率。 故，Gini（D）值越小，数据集D的纯度越高。

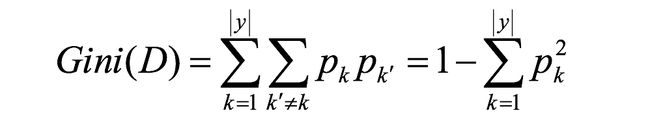
基尼指数Gini_index（D）：一般，选择使划分后基尼系数最小的属性作为最优化分属性。

总结

• ID3 算法
  存在的缺点

​ (1) ID3算法在选择根节点和各内部节点中的分支属性时，采用信息增益作为评价标准。 信息增益的缺点是倾向于选择取值较多的属性，在有些情况下这类属性可能不会提供太多有价值的信息.

​ (2) ID3算法只能对描述属性为离散型属性的数据集构造决策树。

• C4.5算法
  做出的改进(为什么使用C4.5要好)

​ (1) 用信息增益率来选择属性
​ (2) 可以处理连续数值型属性
​ (3)采用了一种后剪枝方法
​ (4)对于缺失值的处理

C4.5算法的优缺点

​ 优点：
​ 产生的分类规则易于理解，准确率较高。

​ 缺点：
​ 在构造树的过程中，需要对数据集进行多次的顺序扫描和排序，因而导致算法的低效。

​ 此外，C4.5只适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时程序无法运行。

• CART算法
  CART算法相比C4.5算法的分类方法，采用了简化的二叉树模型，同时特征选择采用了近似的基尼系数来简化计算。
  C4.5不一定是二叉树，但CART一定是二叉树。

同时，无论是ID3, C4.5还是CART,在做特征选择的时候都是选择最优的一个特征来做分类决策，但是大多数，分类决策不应该是由某一个特征决定的，而是应该由一组特征决定的。 这样决策得到的决策树更加准确。 这个决策树叫做多变量决策树(multi-variate decision tree)。 在选择最优特征的时候，多变量决策树不是选择某一个最优特征，而是选择最优的一个特征线性组合来做决策。 这个算法的代表是OC1，这里不多介绍。

如果样本发生一点点的改动，就会导致树结构的剧烈改变。 这个可以通过集成学习里面的随机森林之类的方法解决。

剪枝

随着树的增长，在训练样集上的精度是单调上升的， 然而在独立的测试样例上测出的精度先上升后下降。

常用方法

• 预剪枝
  （1）每一个结点所包含的最小样本数目，例如10，则该结点总样本数小于10时，则不再分；
  （2）指定树的高度或者深度，例如树的最大深度为4；
  （3）指定结点的熵小于某个值，不再划分。随着树的增长， 在训练样集上的精度是单调上升的， 然而在独立的测试样例上测出的精度先上升后下降。

• 后剪枝：
  后剪枝，在已生成过拟合决策树上进行剪枝，可以得到简化版的剪枝决策树。

特征工程-特征提取

定义：将任意数据（如文本或图像）转换为可用于机器学习的数字特征

• 特征提取分类:
  • 字典特征提取(特征离散化)
  • 文本特征提取
  • 图像特征提取（深度学习将介绍）

字典特征提取api

对字典数据进行特征值化

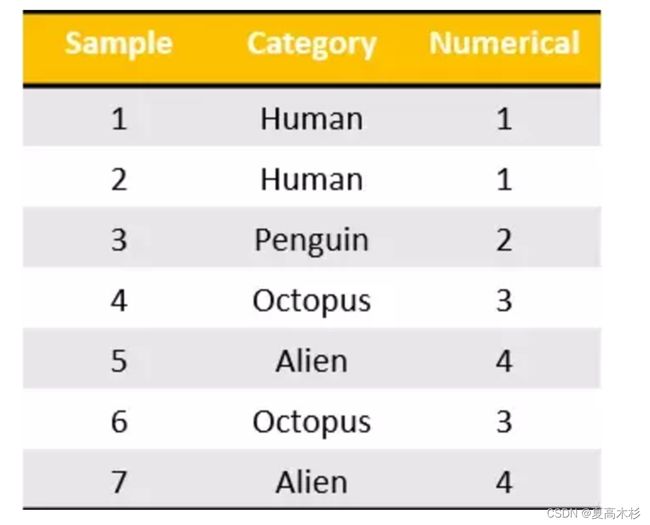
转化为

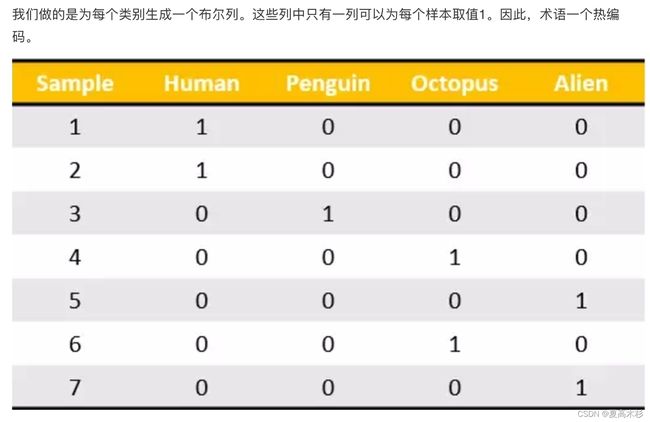
对于特征当中存在类别信息的我们都会做one-hot编码处理

• sklearn.feature_extraction.DictVectorizer(sparse=True,…)
  • DictVectorizer.fit_transform(X)
    • X:字典或者包含字典的迭代器返回值
    • 返回sparse矩阵
  • DictVectorizer.get_feature_names() 返回类别名称

文本特征提取

对文本数据进行特征值化

• sklearn.feature_extraction.text.CountVectorizer(stop_words=[])
  • 返回词频矩阵
  • CountVectorizer.fit_transform(X)
    • X:文本或者包含文本字符串的可迭代对象
    • 返回值:返回sparse矩阵
  • CountVectorizer.get_feature_names() 返回值:单词列表
• sklearn.feature_extraction.text.TfidfVectorizer

jieba分词处理

• jieba.cut()
  • 返回词语组成的生成器

Tf-idf文本特征提取

• TF-IDF的主要思想是：如果某个词或短语在一篇文章中出现的概率高，并且在其他文章中很少出现，则认为此词或者短语具有很好的类别区分能力，适合用来分类。

• TF-IDF作用：用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。

• 词频（term frequency，tf）指的是某一个给定的词语在该文件中出现的频率

• 逆向文档频率（inverse document frequency，idf）是一个词语普遍重要性的度量。某一特定词语的idf，可以由总文件数目除以包含该词语之文件的数目，再将得到的商取以10为底的对数得到
  
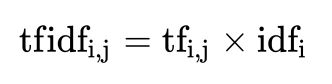
  Tf-idf的重要性：分类机器学习算法进行文章分类中前期数据处理方式

案例

# coding:utf-8

from sklearn.feature_extraction import DictVectorizer
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
import jieba


def dict_demo():
    """
    字典特征提取
    :return:
    """
    data = [{'city': '北京', 'temperature': 100},
            {'city': '上海', 'temperature': 60},
            {'city': '深圳', 'temperature': 30}]
    # 字典特征提取
    # 1.实例化
    transfer = DictVectorizer(sparse=False)

    # 2.调用fit_transform
    trans_data = transfer.fit_transform(data)

    print("特征名字是：\n", transfer.get_feature_names())

    print(trans_data)


def english_count_text_demo():
    """
    文本特征提取 -- 英文
    :return: NOne
    """
    data = ["life is is short,i like python",
            "life is too long,i dislike python"]

    # 1.实例化
    # transfer = CountVectorizer(sparse=False)  # 注意，没有sparse
    transfer = CountVectorizer(stop_words=["dislike"])

    # 2.调用fit_transform
    transfer_data = transfer.fit_transform(data)

    print(transfer.get_feature_names())
    print(transfer_data.toarray())  # 用于看到sparse矩阵


def chinese_count_text_demo1():
    """
    文本特征提取 -- 中文
    :return: NOne
    """
    data = ["人生 苦短, 我 喜欢 Python",
            "生活 太长久, 我 不 喜欢 Python"]

    # 1.实例化
    transfer = CountVectorizer()

    # 2.调用fit_transform
    transfer_data = transfer.fit_transform(data)

    print(transfer.get_feature_names())
    print(transfer_data.toarray())


def cut_word(sen):
    """
    中文分词
    :return: sen
    """
    # print(" ".join(list(jieba.cut(sen))))
    return " ".join(list(jieba.cut(sen)))


def chinese_count_text_demo2():
    """
    文本特征提取 -- 中文
    :return: NOne
    """
    data = ["一种还是一种今天很残酷，明天更残酷，后天很美好，但绝对大部分是死在明天晚上，所以每个人不要放弃今天。",
            "我们看到的从很远星系来的光是在几百万年之前发出的，这样当我们看到宇宙时，我们是在看它的过去。",
            "如果只用一种方式了解某样事物，你就不会真正了解它。了解事物真正含义的秘密取决于如何将其与我们所了解的事物相联系。"]

    list = []
    for temp in data:
        # print(temp)
        list.append(cut_word(temp))
    print(list)

    # 1.实例化
    transfer = CountVectorizer(stop_words=["一种", "还是"])

    # 2.调用fit_transform
    transfer_data = transfer.fit_transform(list)

    print(transfer.get_feature_names())
    print(transfer_data.toarray())


def tfidf_text_demo():
    """
    文本特征提取 -- 中文
    :return: NOne
    """
    data = ["一种还是一种今天很残酷，明天更残酷，后天很美好，但绝对大部分是死在明天晚上，所以每个人不要放弃今天。",
            "我们看到的从很远星系来的光是在几百万年之前发出的，这样当我们看到宇宙时，我们是在看它的过去。",
            "如果只用一种方式了解某样事物，你就不会真正了解它。了解事物真正含义的秘密取决于如何将其与我们所了解的事物相联系。"]

    list = []
    for temp in data:
        # print(temp)
        list.append(cut_word(temp))
    # print(list)

    # 1.实例化
    # transfer = CountVectorizer(stop_words=["一种", "还是"])
    transfer = TfidfVectorizer()

    # 2.调用fit_transform
    transfer_data = transfer.fit_transform(list)

    print(transfer.get_feature_names())
    print(transfer_data.toarray())


if __name__ == '__main__':
    # dict_demo()
    # english_count_text_demo()
    # chinese_count_text_demo1()
    # cut_word("我喜欢你中国")
    chinese_count_text_demo2()
    # tfidf_text_demo()

决策树api

• class sklearn.tree.DecisionTreeClassifier(criterion=’gini’, max_depth=None,random_state=None)
  • criterion
    • 特征选择标准
    • “gini"或者"entropy”，前者代表基尼系数，后者代表信息增益。一默认"gini"，即CART算法。
  • min_samples_split
    • 内部节点再划分所需最小样本数
    • 这个值限制了子树继续划分的条件，如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分。 默认是2.如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。我之前的一个项目例子，有大概10万样本，建立决策树时，我选择了min_samples_split=10。可以作为参考。
  • min_samples_leaf
    • 叶子节点最少样本数
    • 这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝。 默认是1,可以输入最少的样本数的整数，或者最少样本数占样本总数的百分比。如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。之前的10万样本项目使用min_samples_leaf的值为5，仅供参考。
  • max_depth
    • 决策树最大深度
    • 决策树的最大深度，默认可以不输入，如果不输入的话，决策树在建立子树的时候不会限制子树的深度。一般来说，数据少或者特征少的时候可以不管这个值。如果模型样本量多，特征也多的情况下，推荐限制这个最大深度，具体的取值取决于数据的分布。常用的可以取值10-100之间
  • random_state
    • 随机数种子

案例

1. 乘坐班是指乘客班（1，2，3），是社会经济阶层的代表。

2. 其中age数据存在缺失。

import pandas as pd
import numpy as np
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, export_graphviz

data = pd.read_csv("http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt")

# 2.数据基本处理
# 2.1 确定特征值,目标值
x = data[["pclass", "age", "sex"]]
x.head()

y = data["survived"]
y.head()
# 2.2 缺失值处理
x["age"].fillna(value=data["age"].mean(), inplace=True)

# 2.3 数据集划分
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22, test_size=0.2)
# 3.特征工程(字典特征抽取)
x_train = x_train.to_dict(orient="records")
x_test = x_test.to_dict(orient="records")

"""
# 对于x转换成字典数据x.to_dict(orient="records")
# [{"pclass": "1st", "age": 29.00, "sex": "female"}, {}]

transfer = DictVectorizer(sparse=False)

x_train = transfer.fit_transform(x_train.to_dict(orient="records"))
x_test = transfer.fit_transform(x_test.to_dict(orient="records"))
"""

# 4.机器学习(决策树)
estimator = DecisionTreeClassifier(criterion="entropy", max_depth=5)
estimator.fit(x_train, y_train)

# 5.模型评估
estimator.score(x_test, y_test)

estimator.predict(x_test)

# 可视化
export_graphviz(estimator, out_file="./data/tree.dot", feature_names=['age', 'pclass=1st', 'pclass=2nd', 'pclass=3rd', '女性', '男性'])

决策树可视化

保存树的结构到dot文件

• sklearn.tree.export_graphviz() 该函数能够导出DOT格式
  • tree.export_graphviz(estimator,out_file='tree.dot’,feature_names=[‘’,’’])

把文件内的内容复制到网站内生成图
http://webgraphviz.com/

总结

• 优点：简单的理解和解释，树木可视化。
• 缺点：决策树学习者可以创建不能很好地推广数据的过于复杂的树,容易发生过拟合。
• 改进：
  • 减枝cart算法
  • 随机森林（集成学习的一种）

注：企业重要决策，由于决策树很好的分析能力，在决策过程应用较多， 可以选择特征

5. 集成学习

集成学习通过建立几个模型来解决单一预测问题。它的工作原理是生成多个分类器/模型，各自独立地学习和作出预测。这些预测最后结合成组合预测，因此优于任何一个单分类的做出预测。



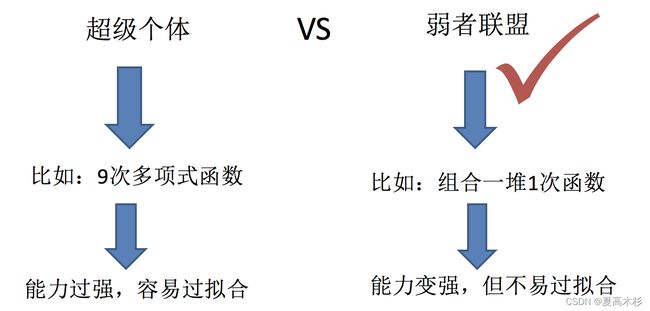
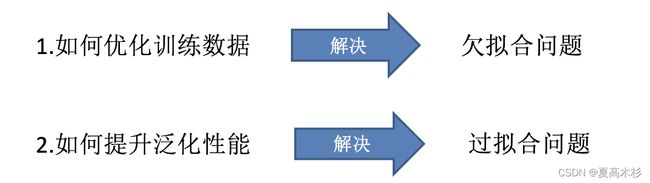
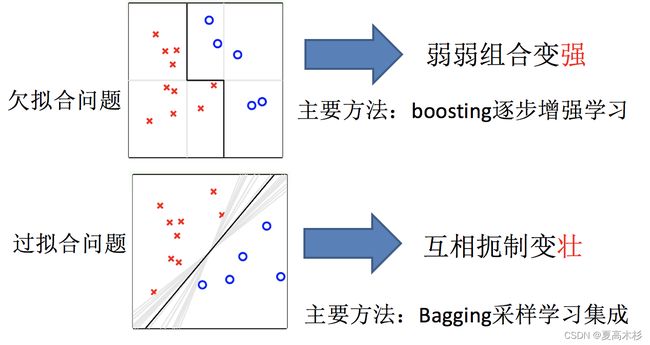
只要单分类器的表现不太差，集成学习的结果总是要好于单分类器的.

Bagging和随机森林

Bagging集成原理

目标：将样本进行分类

实现过程

1. 不同的分类器采样不同的数据集
2. 训练分类器
3. 各个分类器平权投票获取最终结果

随机森林

在机器学习中，随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。

随机森林 = Bagging + 决策树

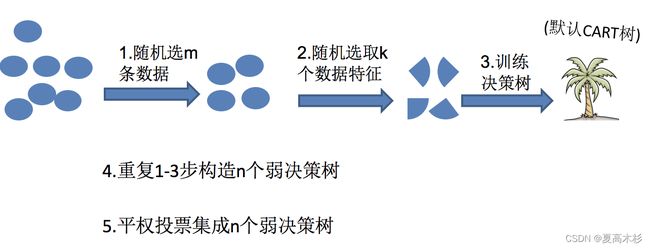
随机森林够造过程中的关键步骤（用N来表示训练用例（样本）的个数，M表示特征数目）：
​ 1）一次随机选出一个样本，有放回的抽样，重复N次（有可能出现重复的样本）
​ 2） 随机去选出m个特征, m <

思考
1.为什么要随机抽样训练集？　　
如果不进行随机抽样，每棵树的训练集都一样，那么最终训练出的树分类结果也是完全一样的
2.为什么要有放回地抽样？
如果不是有放回的抽样，那么每棵树的训练样本都是不同的，都是没有交集的，这样每棵树都是“有偏的”，都是绝对“片面的”（当然这样说可能不对），也就是说每棵树训练出来都是有很大的差异的；而随机森林最后分类取决于多棵树（弱分类器）的投票表决。

api

• sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None, min_samples_split=2)
  • n_estimators：integer，optional（default = 10）森林里的树木数量120,200,300,500,800,1200
  • Criterion：string，可选（default =“gini”）分割特征的测量方法
  • max_depth：integer或None，可选（默认=无）树的最大深度 5,8,15,25,30
  • max_features="auto”,每个决策树的最大特征数量
    • If “auto”, then max_features=sqrt(n_features).
    • If “sqrt”, then max_features=sqrt(n_features)(same as “auto”).
    • If “log2”, then max_features=log2(n_features).
    • If None, then max_features=n_features.
  • bootstrap：boolean，optional（default = True）是否在构建树时使用放回抽样
  • min_samples_split:节点划分最少样本数
  • min_samples_leaf:叶子节点的最小样本数
• 超参数：n_estimator, max_depth, min_samples_split,min_samples_leaf

案例

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.feature_extraction import DictVectorizer
# from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.ensemble import RandomForestClassifier

# 1.获取数据
data = pd.read_csv("http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt")

# 2.数据基本处理
# 2.1 确定特征值,目标值
x = data[["pclass", "age", "sex"]]
y = data["survived"]
# 2.2 缺失值处理
x["age"].fillna(value=data["age"].mean(), inplace=True)

# 2.3 数据集划分
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22, test_size=0.2)
# 3.特征工程(字典特征抽取)
transfer = DictVectorizer()

x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)

# 4.机器学习（模型训练）
estimator = RandomForestClassifier()

param_grid = {"n_estimators": [120,200,300,500,800,1200], "max_depth": [5, 8, 15, 25, 30]}

# 超参数调优   网格搜索
estimator = GridSearchCV(estimator, param_grid=param_grid, cv=5)

estimator.fit(x_train, y_train)
estimator.score(x_test, y_test)   
print("随机森林预测的准确率为：", estimator.score(x_test, y_test))

注意

• 随机森林的建立过程
• 树的深度、树的个数等需要进行超参数调优

bagging集成优点

​ Bagging + 决策树/线性回归/逻辑回归/深度学习… = bagging集成学习方法

经过上面方式组成的集成学习方法:

1. 均可在原有算法上提高约2%左右的泛化正确率
2. 简单, 方便, 通用

Boosting

boosting集成原理

随着学习的积累从弱到强

简而言之：每新加入一个弱学习器，整体能力就会得到提升

代表算法：Adaboost，GBDT，XGBoost

实现过程：

1. 训练第一个学习器
2. 调整数据分布
3. 训练第二个学习器
4. 再次调整数据分布
5. 依次训练学习器，调整数据分布
6. 整体过程实现

关键点：


AdaBoost的构造过程小结

api
from sklearn.ensemble import AdaBoostClassifier

api链接:https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.AdaBoostClassifier.html#sklearn.ensemble.AdaBoostClassifier

bagging集成与boosting集成的区别：

• 区别一:数据方面
  • Bagging：对数据进行采样训练；
  • Boosting：根据前一轮学习结果调整数据的重要性。
• 区别二:投票方面
  • Bagging：所有学习器平权投票；
  • Boosting：对学习器进行加权投票。
• 区别三:学习顺序
  • Bagging的学习是并行的，每个学习器没有依赖关系；
  • Boosting学习是串行，学习有先后顺序。
• 区别四:主要作用
  • Bagging主要用于提高泛化性能（解决过拟合，也可以说降低方差）
  • Boosting主要用于提高训练精度 （解决欠拟合，也可以说降低偏差）

GBDT(了解)

梯度提升决策树(GBDT Gradient Boosting Decision Tree) 是一种迭代的决策树算法，该算法由多棵决策树组成，所有树的结论累加起来做最终答案。它在被提出之初就被认为是泛化能力（generalization)较强的算法。近些年更因为被用于搜索排序的机器学习模型而引起大家关注。

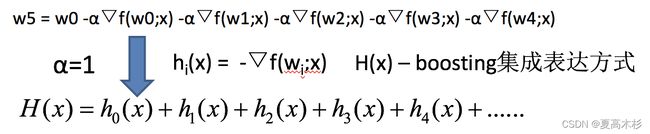
如果上式中的hi(x)=决策树模型,则上式就变为:
GBDT = 梯度下降 + Boosting + 决策树

例子：

GBDT主要执行思想
1.使用梯度下降法优化代价函数；
2.使用一层决策树作为弱学习器，负梯度作为目标值；
3.利用boosting思想进行集成。

XGBoost【了解】

XGBoost= 二阶泰勒展开+boosting+决策树+正则化

面试题：了解XGBoost么，请详细说说它的原理
回答要点：二阶泰勒展开，boosting，决策树，正则化

Boosting：XGBoost使用Boosting提升思想对多个弱学习器进行迭代式学习

二阶泰勒展开：每一轮学习中，XGBoost对损失函数进行二阶泰勒展开，使用一阶和二阶梯度进行优化。

决策树：在每一轮学习中，XGBoost使用决策树算法作为弱学习进行优化。

正则化：在优化过程中XGBoost为防止过拟合，在损失函数中加入惩罚项，限制决策树的叶子节点个数以及决策树叶子节点的值。

6. 聚类

一种典型的无监督学习算法，主要用于将相似的样本自动归到一个类别中。

在聚类算法中根据样本之间的相似性，将样本划分到不同的类别中，对于不同的相似度计算方法，会得到不同的聚类结果，常用的相似度计算方法有欧式距离法。

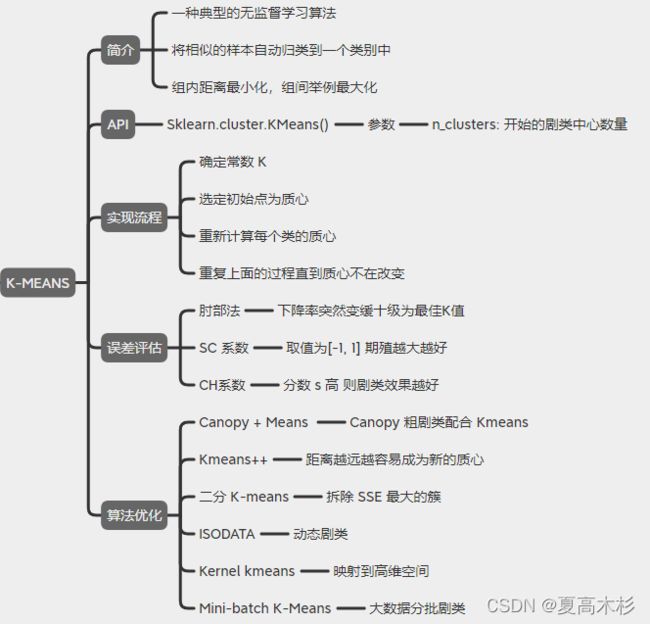
K-means聚类api

• sklearn.cluster.KMeans(n_clusters=8)
  • 参数:
    • n_clusters:开始的聚类中心数量
      • 整型，缺省值=8，生成的聚类数，即产生的质心（centroids）数。
  • 方法:
    • estimator.fit(x)
    • estimator.predict(x)
    • estimator.fit_predict(x)
      • 计算聚类中心并预测每个样本属于哪个类别,相当于先调用fit(x),然后再调用predict(x)

案例

import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import calinski_harabaz_score

# 创建数据集
# X为样本特征，Y为样本簇类别， 共1000个样本，每个样本4个特征，共4个簇，
# 簇中心在[-1,-1], [0,0],[1,1], [2,2]， 簇方差分别为[0.4, 0.2, 0.2, 0.2]
X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
                  cluster_std=[0.4, 0.2, 0.2, 0.2],
                  random_state=9)

# 数据集可视化
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.show()

y_pred = KMeans(n_clusters=2, random_state=9).fit_predict(X)
# 分别尝试n_cluses=2\3\4,然后查看聚类效果
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()

# 用Calinski-Harabasz Index评估的聚类分数
print(calinski_harabaz_score(X, y_pred))

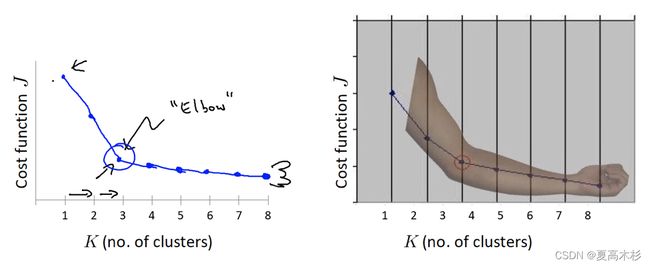
k-means聚类算法实现流程

• k-means其实包含两层内容：

• K : 初始中心点个数（计划聚类数）

• means：求中心点到其他数据点距离的平均值

• 流程：

  1. 事先确定常数K，常数K意味着最终的聚类类别数;
  2. 首先随机选定初始点为质心，并通过计算每一个样本与质心之间的相似度(这里为欧式距离)，将样本点归到最相似的类中，
  3. 接着，重新计算每个类的质心(即为类中心)，重复这样的过程，直到质心不再改变，
  4. 最终就确定了每个样本所属的类别以及每个类的质心。
  • 注意：由于每次都要计算所有的样本与每一个质心之间的相似度，故在大规模的数据集上，K-Means算法的收敛速度比较慢。

k-means模型评估

0. 误差平方和(SSE)

1. 肘部法：​ 下降率突然变缓时即认为是最佳的k值
   

2. SC系数(轮廓系数法)：取值为[-1, 1]，其值越大越好
   结合了聚类的凝聚度（Cohesion）和分离度（Separation），用于评估聚类的效果：
   
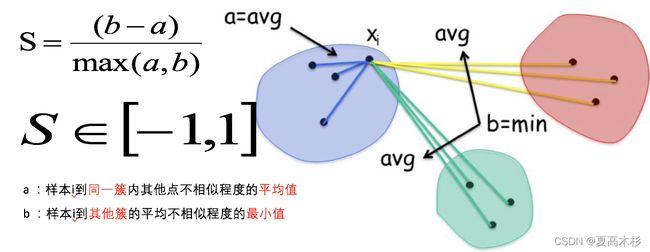
   每次聚类后，每个样本都会得到一个轮廓系数，当它为1时，说明这个点与周围簇距离较远，结果非常好，当它为0，说明这个点可能处在两个簇的边界上，当值为负时，暗含该点可能被误分了。

3. CH系数：分数s高则聚类效果越好
   
   tr为矩阵的迹, Bk为类别之间的协方差矩阵，Wk为类别内部数据的协方差矩阵;

k-means聚类算法优化

优点：

1. 原理简单（靠近中心点），实现容易
2. 聚类效果中上（依赖K的选择）
3. 空间复杂度o(N)，时间复杂度o(IKN)
   • N为样本点个数，K为中心点个数，I为迭代次数

缺点：

1. 对离群点，噪声敏感 （中心点易偏移）
2. 很难发现大小差别很大的簇及进行增量计算
3. 结果不一定是全局最优，只能保证局部最优（与K的个数及初值选取有关）

优化方法	思路
Canopy+kmeans	Canopy粗聚类配合kmeans
kmeans++	距离越远越容易成为新的质心
二分k-means	拆除SSE最大的簇
k-medoids	和kmeans选取中心点的方式不同
kernel kmeans	映射到高维空间
ISODATA	动态聚类
Mini-batch K-Means	大数据集分批聚类

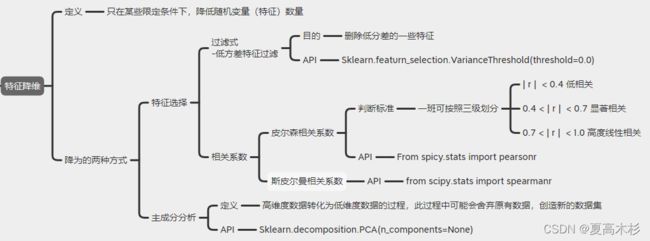
特征工程-特征降维

降维是指在某些限定条件下，降低随机变量(特征)个数，得到一组**“不相关”主变量**的过程

两种方式

• 特征选择
• 主成分分析（可以理解一种特征提取的方式）

特征选择

数据中包含冗余或无关变量（或称特征、属性、指标等），旨在从原有特征中找出主要特征。

• 具体方法：
  • Filter(过滤式)：主要探究特征本身特点、特征与特征和目标值之间关联
    • 方差选择法：低方差特征过滤
    • 相关系数
  • Embedded (嵌入式)：算法自动选择特征（特征与目标值之间的关联）
    • 决策树:信息熵、信息增益
    • 正则化：L1、L2
    • 深度学习：卷积等

低方差特征过滤

删除低方差的一些特征，前面讲过方差的意义。再结合方差的大小来考虑这个方式的角度。

• 特征方差小：某个特征大多样本的值比较相近
• 特征方差大：某个特征很多样本的值都有差别

api

• sklearn.feature_selection.VarianceThreshold(threshold = 0.0)
  • 删除所有低方差特征
  • Variance.fit_transform(X)
    • X:numpy array格式的数据[n_samples,n_features]
    • 返回值：训练集差异低于threshold的特征将被删除。默认值是保留所有非零方差特征，即删除所有样本中具有相同值的特征。

# coding:utf-8

import pandas as pd
from sklearn.feature_selection import VarianceThreshold

def var_thr():
    """
    特征选择：低方差特征过滤
    :return:
    """
    data = pd.read_csv("./data/factor_returns.csv")
    print(data)

    transfer = VarianceThreshold(threshold=10)
    trans_data = transfer.fit_transform(data.iloc[:, 1:10])

    print("之前数据的形状：\n",data.iloc[:, 1:10].shape)
    print("之后数据的形状：\n",trans_data.shape)

    print(trans_data)
    pass





if __name__ == '__main__':
    var_thr()

相关系数

• 主要实现方式：

  • 皮尔逊相关系数
  • 斯皮尔曼相关系数

• 皮尔逊相关系数(Pearson Correlation Coefficient)’
  

• 相关系数的值介于–1与+1之间，即–1≤ r ≤+1。其性质如下：

  • 当r>0时，表示两变量正相关，r<0时，两变量为负相关
  • 当|r|=1时，表示两变量为完全相关，当r=0时，表示两变量间无相关关系
  • 当0<|r|<1时，表示两变量存在一定程度的相关。且|r|越接近1，两变量间线性关系越密切；|r|越接近于0，表示两变量的线性相关越弱
  • 一般可按三级划分：|r|<0.4为低度相关；0.4≤|r|<0.7为显著性相关；0.7≤|r|<1为高度线性相关

api:

• from scipy.stats import pearsonr

  • x : (N,) array_like
  • y : (N,) array_like Returns: (Pearson’s correlation coefficient, p-value)

• 斯皮尔曼相关系数(Rank IC)
  
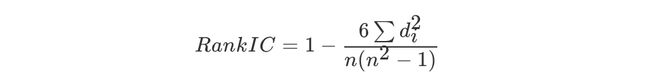
  斯皮尔曼相关系数表明 X (自变量) 和 Y (因变量)的相关方向。 如果当X增加时， Y 趋向于增加, 斯皮尔曼相关系数则为正

与之前的皮尔逊相关系数大小性质一样，取值 [-1, 1]之间

api

from scipy.stats import spearmanr

# coding:utf-8

from scipy.stats import pearsonr, spearmanr

# 皮尔逊演示
x1 = [12.5, 15.3, 23.2, 26.4, 33.5, 34.4, 39.4, 45.2, 55.4, 60.9]
x2 = [21.2, 23.9, 32.9, 34.1, 42.5, 43.2, 49.0, 52.8, 59.4, 63.5]

ret = pearsonr(x1, x2)
print("这两列数据的皮尔逊相关系数为：\n", ret)


ret = spearmanr(x1, x2)
print("这两列数据的斯皮尔曼相关系数为：\n", ret)

主成分分析(PCA)

• 定义：高维数据转化为低维数据的过程，在此过程中可能会舍弃原有数据、创造新的变量
• 作用：是数据维数压缩，尽可能降低原数据的维数（复杂度），损失少量信息。
• 应用：回归分析或者聚类分析当中

api

• sklearn.decomposition.PCA(n_components=None)
  • 将数据分解为较低维数空间
  • n_components:
    • 小数：表示保留百分之多少的信息
    • 整数：减少到多少特征
  • PCA.fit_transform(X) X:numpy array格式的数据[n_samples,n_features]
  • 返回值：转换后指定维度的array

案例

# coding:utf-8

from sklearn.decomposition import PCA

data = [[2, 8, 4, 5],
        [6, 3, 0, 8],
        [5, 4, 9, 1]]

# 1.保留到多少维度
# transfer = PCA(n_components=2)
# trans_data = transfer.fit_transform(data)
# print(trans_data)

# 2.保留信息的百分比
transfer = PCA(n_components=0.95)
transfer_data = transfer.fit_transform(data)
print(transfer_data)

k-means案例

• order_products__prior.csv：订单与商品信息
  • 字段：order_id, product_id, add_to_cart_order, reordered
• products.csv：商品信息
  • 字段：product_id, product_name, aisle_id, department_id
• orders.csv：用户的订单信息
  • 字段：order_id,user_id,eval_set,order_number,….
• aisles.csv：商品所属具体物品类别
  • 字段： aisle_id, aisle

import pandas as pd
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score

# 1.获取数据
order_product = pd.read_csv("./data/instacart/order_products__prior.csv")
products = pd.read_csv("./data/instacart/products.csv")
orders = pd.read_csv("./data/instacart/orders.csv")
aisles = pd.read_csv("./data/instacart/aisles.csv")

# 2.数据基本处理
# 2.1 合并表格
table1 = pd.merge(order_product, products, on=["product_id", "product_id"])
table2 = pd.merge(table1, orders, on=["order_id", "order_id"])
table = pd.merge(table2, aisles, on=["aisle_id", "aisle_id"])

# 2.2 交叉表合并
data = pd.crosstab(table["user_id"], table["aisle"])
# 2.3 数据截取
new_data = data[:1000]
# 3.特征工程 — pca
transfer = PCA(n_components=0.9)
trans_data = transfer.fit_transform(new_data)
# 4.机器学习（k-means）
estimator = KMeans(n_clusters=5)
y_pre = estimator.fit_predict(trans_data)
# 5.模型评估
silhouette_score(trans_data, y_pre)