互联网服务客户流失分析（个人练习+源代码）

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

plt.rcParams['font.family'] = ['SimHei']    # 显示中文,解决图中无法显示中文的问题
plt.rcParams['axes.unicode_minus']=False

# 导入数据
data = pd.read_csv('internet_service_churn.csv')

# 查看数据大小
data.shape

(72274, 11)

# 查看前五行
data.head()

	id	is_tv_subscriber	is_movie_package_subscriber	subscription_age	bill_avg	reamining_contract	service_failure_count	download_avg	upload_avg	download_over_limit	churn
0	15	1	0	11.95	25	0.14	0	8.4	2.3	0	0
1	18	0	0	8.22	0	NaN	0	0.0	0.0	0	1
2	23	1	0	8.91	16	0.00	0	13.7	0.9	0	1
3	27	0	0	6.87	21	NaN	1	0.0	0.0	0	1
4	34	0	0	6.39	0	NaN	0	0.0	0.0	0	1

# 查看基本信息
data.info()

RangeIndex: 72274 entries, 0 to 72273
Data columns (total 11 columns):
 #   Column                       Non-Null Count  Dtype  
---  ------                       --------------  -----  
 0   id                           72274 non-null  int64  
 1   is_tv_subscriber             72274 non-null  int64  
 2   is_movie_package_subscriber  72274 non-null  int64  
 3   subscription_age             72274 non-null  float64
 4   bill_avg                     72274 non-null  int64  
 5   reamining_contract           50702 non-null  float64
 6   service_failure_count        72274 non-null  int64  
 7   download_avg                 71893 non-null  float64
 8   upload_avg                   71893 non-null  float64
 9   download_over_limit          72274 non-null  int64  
 10  churn                        72274 non-null  int64  
dtypes: float64(4), int64(7)
memory usage: 6.1 MB

# 为特征重命名
data.columns = ['用户标识', '是否为电视订阅用户', '是否为电影包订阅用户', '客户年限', '平均账单金额',
               '合同剩余年限', '投诉次数', '平均下载量', '平均上传量', '下载超过限制', '是否流失']

字段解释：

用户标识：唯一的用户id

是否为电视订阅用户：用户是否有电视订阅，是为1，否则为0

是否为电影包订阅用户：用户是否有电影套餐，是为1，否则为0

客户年限：客户使用我们的服务多少年

平均账单金额：过去3个月账单平均消费

合同剩余年限：客户合同还剩多少年？如果为空，代表客户没有合同。

投诉次数：过去3个月客户因服务失败，而呼叫服务中心的次数

平均下载量：过去3个月的互联网下载情况(GB)

平均上传量：过去3个月平均上传量(GB)

下载超过限制：大多数客户都有下载限制。如果他们达到了这个极限，他们必须为此付费

是否流失：用户是否取消了服务

# 查看缺失值
data.isnull().sum()

用户标识              0
是否为电视订阅用户         0
是否为电影包订阅用户        0
客户年限              0
平均账单金额            0
合同剩余年限        21572
投诉次数              0
平均下载量           381
平均上传量           381
下载超过限制            0
是否流失              0
dtype: int64

# 这里使用0进行填充，这里认为空值为没有合同，因此将合同剩余年限设置为0
# 下载量和上传量在0处分布最多，同样使用0进行填充
data = data.fillna(0)

# 观察数据是否有重复值
data.duplicated().sum()

0

# 对分类型变量和连续型变量进行区分
col_c = ['是否为电视订阅用户', '是否为电影包订阅用户', '投诉次数', '下载超过限制', '是否流失']
col_n = ['客户年限', '平均账单金额', '合同剩余年限', '平均下载量', '平均上传量']

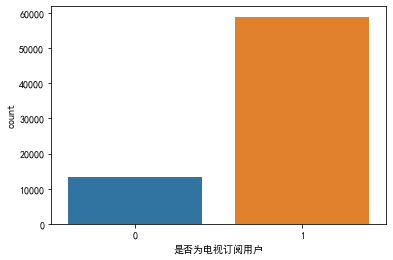
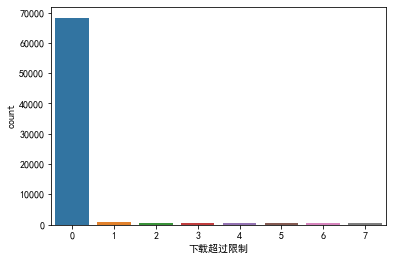
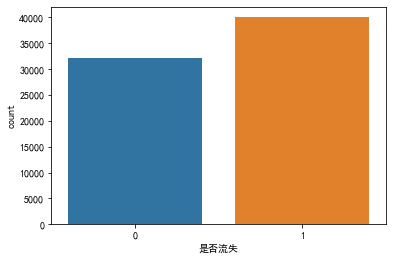
# 查看分类型特征分布情况
for i in col_c:
    plt.figure(figsize=(6,4))
    sns.countplot(x=i, data=data)

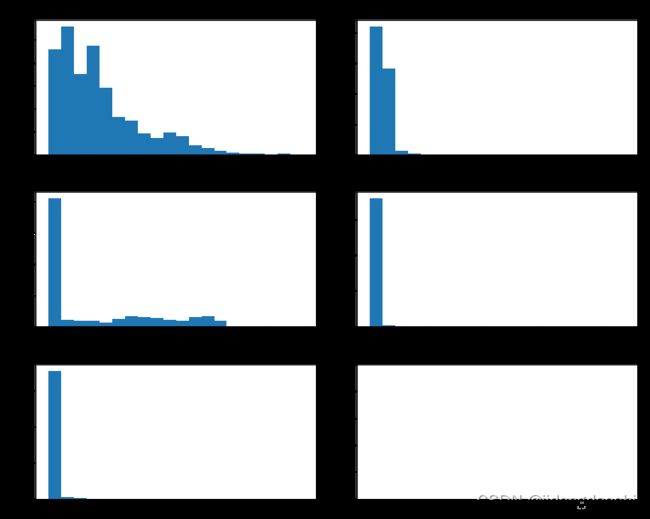
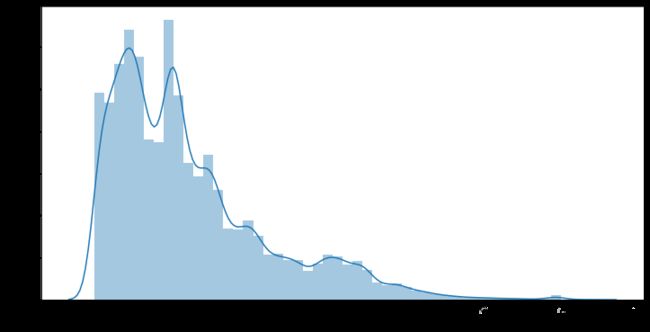
# 查看连续型特征分布情况
fig, ax = plt.subplots(3,2,figsize=(10,8))
axes = ax.flatten()
for i in range(len(col_n)):
    axes[i].hist(x=data[col_n[i]], bins=20)
    axes[i].set_title(col_n[i])
plt.tight_layout()

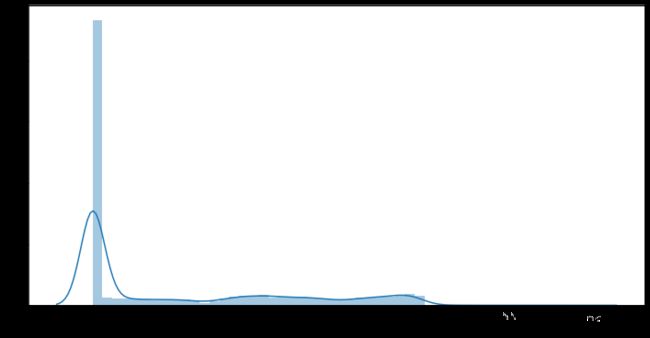
# 用seaborn绘图
for i in col_n:
    plt.figure(figsize=(12,6))
    sns.distplot(data[i], kde=True)

# 描述性统计
data.describe()

	用户标识	是否为电视订阅用户	是否为电影包订阅用户	客户年限	平均账单金额	合同剩余年限	投诉次数	平均下载量	平均上传量	下载超过限制	是否流失
count	7.227400e+04	72274.000000	72274.000000	72274.000000	72274.000000	72274.000000	72274.000000	72274.000000	72274.000000	72274.000000	72274.000000
mean	8.463182e+05	0.815259	0.334629	2.450051	18.942483	0.502319	0.274234	43.459595	4.169977	0.207613	0.554141
std	4.891022e+05	0.388090	0.471864	2.034990	13.215386	0.669524	0.816621	63.317706	9.797685	0.997123	0.497064
min	1.500000e+01	0.000000	0.000000	-0.020000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
25%	4.222165e+05	1.000000	0.000000	0.930000	13.000000	0.000000	0.000000	6.400000	0.500000	0.000000	0.000000
50%	8.477840e+05	1.000000	0.000000	1.980000	19.000000	0.000000	0.000000	27.500000	2.100000	0.000000	1.000000
75%	1.269562e+06	1.000000	1.000000	3.300000	22.000000	1.040000	0.000000	60.200000	4.800000	0.000000	1.000000
max	1.689744e+06	1.000000	1.000000	12.800000	406.000000	2.920000	19.000000	4415.200000	453.300000	7.000000	1.000000

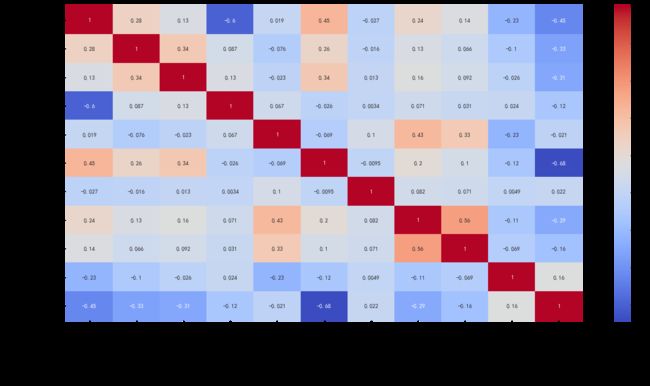
# 作热力图探究特征相关性
# 可以看出下载超过限制次数和投诉次数与流失呈正相关性，订阅、剩余年限、上传下载数量等于流失呈负相关，这符合我们的认知
corr = data.corr()
plt.figure(figsize=(20, 10))
sns.heatmap(corr, annot=True, cmap='coolwarm')

# 提取自变量和因变量
X = data[['是否为电视订阅用户', '是否为电影包订阅用户', '投诉次数', '下载超过限制', '客户年限', 
         '平均账单金额', '合同剩余年限', '平均下载量', '平均上传量']]
y = data[['是否流失']]

from sklearn.preprocessing import StandardScaler

# 对数据进行标准化处理
ss = StandardScaler()
X = ss.fit_transform(X)
y = np.ravel(y)

# 切分训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

# 导入KNN模型
from sklearn.neighbors import KNeighborsClassifier
model = KNeighborsClassifier() # 实例化
model.fit(X_train,y_train) # 拟合
model_pre = model.predict(X_test) # 预测测试集结果

# 导入accuracy库
from sklearn.metrics import accuracy_score
print('准确率为{}'.format(accuracy_score(y_test, model_pre)))

准确率为0.9076318556643976

con = pd.concat([pd.pivot_table(data, index='是否流失', values='用户标识', aggfunc='count'), 
                 pd.pivot_table(data, index='是否流失', aggfunc='mean').drop(['用户标识'], axis=1)], axis=1).reset_index()
con

	是否流失	用户标识	下载超过限制	合同剩余年限	客户年限	平均上传量	平均下载量	平均账单金额	投诉次数	是否为电影包订阅用户	是否为电视订阅用户
0	0	32224	0.031622	1.011077	2.727828	5.912817	64.117565	19.252731	0.254593	0.496214	0.956989
1	1	40050	0.349213	0.092976	2.226554	2.767698	26.838312	18.692859	0.290037	0.204619	0.701223

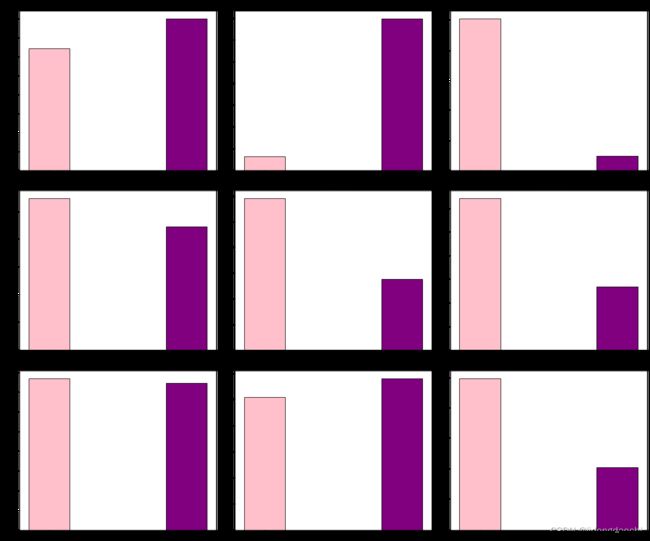
# 查看流失用户和非流失用户的不同特征
col = ['用户标识', '下载超过限制', '合同剩余年限', '客户年限', '平均上传量', '平均下载量', '平均账单金额', '投诉次数', '是否为电影包订阅用户', '是否为电视订阅用户']
fig, ax = plt.subplots(3, 3, figsize=(18,15))
axes = ax.flatten()
for i in range(len(col) - 1):
    axes[i].bar(x='是否流失', height=col[i], data=con, width=0.3, color=['pink', 'purple'], edgecolor='black', tick_label=[0, 1])
    axes[i].set_title(col[i])
plt.tight_layout()

# 获取流失用户数据
churn = data[data['是否流失']==1].reset_index(drop=True)
churn.head()

	用户标识	是否为电视订阅用户	是否为电影包订阅用户	客户年限	平均账单金额	合同剩余年限	投诉次数	平均下载量	平均上传量	下载超过限制	是否流失
0	18	0	0	8.22	0	0.0	0	0.0	0.0	0	1
1	23	1	0	8.91	16	0.0	0	13.7	0.9	0	1
2	27	0	0	6.87	21	0.0	1	0.0	0.0	0	1
3	34	0	0	6.39	0	0.0	0	0.0	0.0	0	1
4	71	0	0	8.96	18	0.0	0	21.3	2.0	0	1

churn.describe()

	用户标识	是否为电视订阅用户	是否为电影包订阅用户	客户年限	平均账单金额	合同剩余年限	投诉次数	平均下载量	平均上传量	下载超过限制	是否流失
count	4.005000e+04	40050.000000	40050.000000	40050.000000	40050.000000	40050.000000	40050.000000	40050.000000	40050.000000	40050.000000	40050.0
mean	6.483943e+05	0.701223	0.204619	2.226554	18.692859	0.092976	0.290037	26.838312	2.767698	0.349213	1.0
std	4.322926e+05	0.457727	0.403428	1.709438	13.073794	0.339111	0.865134	46.137197	7.932245	1.290545	0.0
min	1.800000e+01	0.000000	0.000000	-0.020000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	1.0
25%	2.863745e+05	0.000000	0.000000	0.980000	13.000000	0.000000	0.000000	0.000000	0.000000	0.000000	1.0
50%	5.907300e+05	1.000000	0.000000	1.970000	20.000000	0.000000	0.000000	11.900000	0.900000	0.000000	1.0
75%	9.498655e+05	1.000000	0.000000	2.940000	23.000000	0.000000	0.000000	36.700000	2.900000	0.000000	1.0
max	1.689744e+06	1.000000	1.000000	12.800000	278.000000	2.310000	19.000000	1706.200000	327.200000	7.000000	1.0

# C(合同状态) = 合同剩余年限	
# M(消费金额) = 平均下载量 + 平均上传量 + 平均账单金额
# A(活跃度) = 是否为电视订阅用户 + 是否为电影包订阅用户
# S(满意度) = 投诉次数 + 下载超过限制
# L(服务时长) = 客户年限
# 进行特征组合

clf = {
    'C':churn['合同剩余年限'],
    'M':churn['平均下载量'] + churn['平均上传量'] + churn['平均账单金额'],
    'A':churn['是否为电视订阅用户'] + churn['是否为电影包订阅用户'],
    'S':churn['投诉次数'] + churn['下载超过限制'],
    'L':churn['客户年限']
}

data_clf = pd.DataFrame(clf)
data_clf

	C	M	A	S	L
0	0.00	0.0	0	0	8.22
1	0.00	30.6	1	0	8.91
2	0.00	21.0	0	1	6.87
3	0.00	0.0	0	0	6.39
4	0.00	41.3	0	0	8.96
...	...	...	...	...	...
40045	1.25	0.0	2	0	0.09
40046	1.63	1.8	1	0	0.06
40047	2.19	1.7	1	0	0.02
40048	0.72	0.0	0	0	0.01
40049	0.82	0.0	2	0	0.01

40050 rows × 5 columns

# 对新数据进行标准化
data_clf = ss.fit_transform(data_clf)
data_clf = pd.DataFrame(data_clf, columns=['C', 'M', 'A', 'S', 'L'])
data_clf

	C	M	A	S	L
0	-0.274177	-0.835332	-1.288250	-0.411060	3.506135
1	-0.274177	-0.306103	0.133906	-0.411060	3.909781
2	-0.274177	-0.472136	-1.288250	0.231974	2.716392
3	-0.274177	-0.835332	-1.288250	-0.411060	2.435594
4	-0.274177	-0.121046	-1.288250	-0.411060	3.939031
...	...	...	...	...	...
40045	3.411973	-0.835332	1.556063	-0.411060	-1.249873
40046	4.532562	-0.804201	0.133906	-0.411060	-1.267422
40047	6.183957	-0.805931	0.133906	-0.411060	-1.290822
40048	1.849045	-0.835332	-1.288250	-0.411060	-1.296672
40049	2.143937	-0.835332	1.556063	-0.411060	-1.296672

40050 rows × 5 columns

# 导入聚类相关库
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score

# 通过学习曲线选择一个合适簇数
scores = []
inertias = []

for i in range(2,10):
    kmeans = KMeans(n_clusters=i, random_state=42)
    kmeans.fit(data_clf)
    score = silhouette_score(data_clf, kmeans.labels_, sample_size=180)
    scores.append(score)
    inertias.append(kmeans.inertia_)

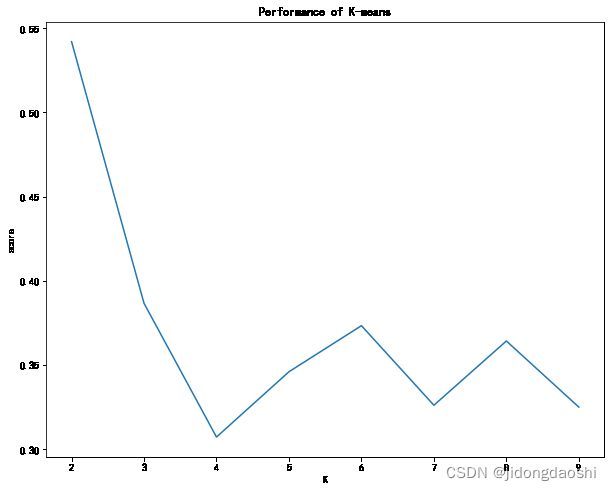
plt.figure(figsize=(10, 8))
plt.plot(range(2,10), scores)
plt.xlabel('K')
plt.ylabel('score')
plt.title('Performance of K-means')

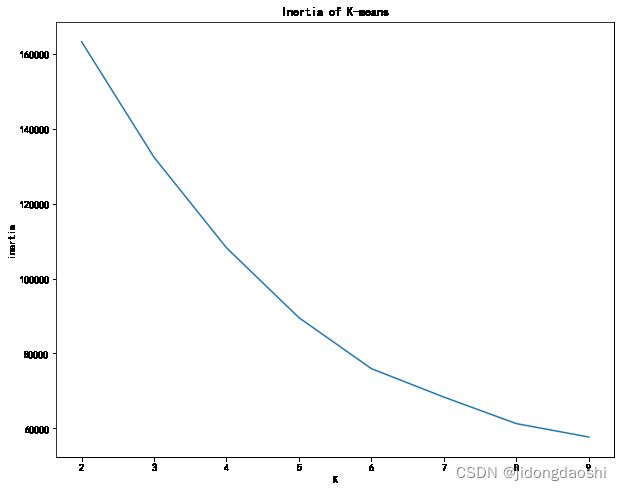
plt.figure(figsize=(10, 8))
plt.plot(range(2,10), inertias)
plt.xlabel('K')
plt.ylabel('inertia')
plt.title('Inertia of K-means')
plt.show()

# 设定簇数为6，并获取标签以及簇心
model = KMeans(n_clusters=6, random_state=42)
model.fit(data_clf)

centers = model.cluster_centers_
labels = model.labels_

#将六个簇心转换成DataFrame
centers = pd.DataFrame(centers, columns=['C', 'M', 'A', 'S', 'L'])
centers

	C	M	A	S	L
0	-0.218828	0.075537	0.313688	-0.227904	1.782962
1	-0.237469	-0.094478	0.480242	-0.257323	-0.375447
2	3.753665	0.238278	0.508351	-0.154067	-0.280738
3	-0.255118	-0.252971	-1.288250	-0.220537	-0.298799
4	-0.203795	-0.555980	-0.037028	3.214076	0.172612
5	-0.114658	3.300728	0.133906	-0.074866	-0.072260

# 将用户类型和人数转换成DataFrame类型
labels = pd.DataFrame(labels, columns=['用户类型'])
labels = pd.DataFrame(labels.value_counts()).sort_index().reset_index()
labels = labels.rename(columns={0:'人数'})

# 合并数据
final = pd.concat([labels, centers], axis=1)
final['用户类型'] = ['class_1','class_2','class_3','class_4','class_5','class_6']
final

	用户类型	人数	C	M	A	S	L
0	class_1	5659	-0.218828	0.075537	0.313688	-0.227904	1.782962
1	class_2	18663	-0.237469	-0.094478	0.480242	-0.257323	-0.375447
2	class_3	2332	3.753665	0.238278	0.508351	-0.154067	-0.280738
3	class_4	9322	-0.255118	-0.252971	-1.288250	-0.220537	-0.298799
4	class_5	2679	-0.203795	-0.555980	-0.037028	3.214076	0.172612
5	class-6	1395	-0.114658	3.300728	0.133906	-0.074866	-0.072260

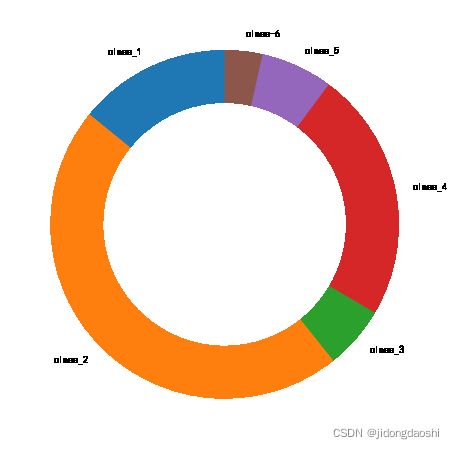
# 绘制环形图
plt.figure(figsize=(8, 8))
plt.pie(final['人数'], wedgeprops={'width':0.3}, startangle=90, labels=final['用户类型'])
plt.show()

# 绘制用户类型和CMASL的关系热力图
plt.figure(figsize=(15,6))
sns.heatmap(data=centers, xticklabels=centers.columns, yticklabels = final["用户类型"], annot=True, cmap='coolwarm')

# 将数据转换成字典结构
results = centers.to_dict('records')

# 将极坐标根据数据长度进行等分
data_length = len(results[0])
angles = np.linspace(0, 2*np.pi, data_length, endpoint=False)
labels = [key for key in results[0].keys()]
score = [[v for v in result.values()] for result in results]

# 使雷达图数据封闭
class_all = []
for i in range(6):
    class_0 = np.concatenate((score[i], [score[i][0]]))
    class_all.append(class_0)

angles = np.concatenate((angles, [angles[0]]))
labels = np.concatenate((labels, [labels[0]]))

# 设置图形的大小
fig = plt.figure(figsize=(8, 6), dpi=100)
# 新建一个子图
ax = plt.subplot(111, polar=True)
# 绘制雷达图
for i in range(6):
    ax.plot(angles, class_all[i])
    
# 设置雷达图中每一项的标签显示
ax.set_thetagrids(angles*180/np.pi, labels)

# 设置雷达图的0度起始位置
ax.set_theta_zero_location('N')

# 设置雷达图的坐标值显示角度，相对于起始角度的偏移量
ax.set_rlabel_position(270)

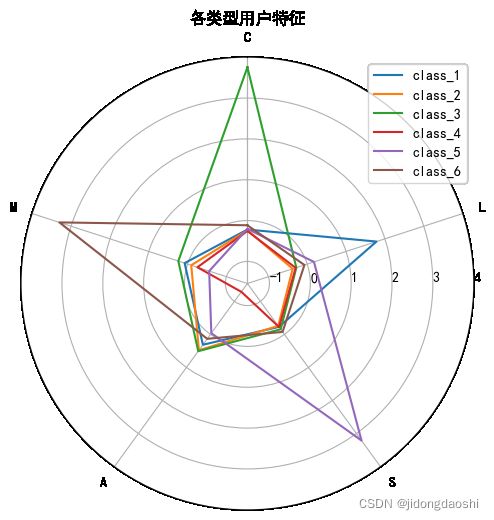
ax.set_title('各类型用户特征')
plt.legend(['class_1','class_2','class_3','class_4','class_5','class_6'], loc='best')
plt.show()

计算公式：

C(合同状态) = 合同剩余年限
M(消费金额) = 平均下载量 + 平均上传量 + 平均账单金额
A(活跃度) = 是否为电视订阅用户 + 是否为电影包订阅用户
S(满意度) = 投诉次数 + 下载超过限制
L(服务时长) = 客户年限

聚类分析&策略建议：

（1）class_1:
    · 在“L”维度明显很高，其他4个维度表现一般
    · 表明这类流失客户是服务年限较长的老客户
    · 一般来说，丢失一个老客户付出的成本是很高的，建议针对这些老客户做一些抽样回访和调研，或许他们能提供很多用户视角的有效建议
（2）class_2:
    · 各个维度不是特别突出，相对来说“A”维度会较高一些
    · 表明他们订阅了电视或者电影套餐，但是没有表现出其他的特征
    · 这类客户虽然特征不明显，但是占比权重最大，属于自然流失群体。
（3）class_3:
    · 在“C”维度表现突出，在“S”和“L”维度相对较低
    · 从相关系数上看，订阅合同是避免流失的最重要因素，而这类客户很多都是已经签署了contract的客户，他们的消费水平、活跃度、满意度也比较高，客户年限上表现得较为年轻，表明他们虽然人数不多，但是属于潜力客户。
    · 建议将这类客户标记为“种子用户”，对他们做好重点维护
（4）class_4:
    · 这类客户人数占比较大，在“A”维度明显短缺
    · 表明这类客户属于没有或很少订阅过电视或者电影套餐服务的群体
    · 建议对这类客户增加订阅服务的次数，或者推送一些订阅服务指南之类的内容，打开他们使用产品的基本操作。
（5）class_5:
    · 在“S”维度表现突出，在“M”维度明显短缺
    · 表明这类客户属于的满意度较低，且不爱消费的客户
    · 可能这些客户不喜欢这款产品，他们产出的消费价值较低，在流失客户中占比也较低，建议可以战略性放弃。
（6）class_6:
    · 在“M”维度表现突出
    · 表明这类客户属于具有明显消费能力，平时下载和上传需求较大的客户群体
    · 建议加强对这类客户的推荐系统配置，例如更精准地判断他们的喜好，更高频率地推送相关内容，满足他们的大量需求