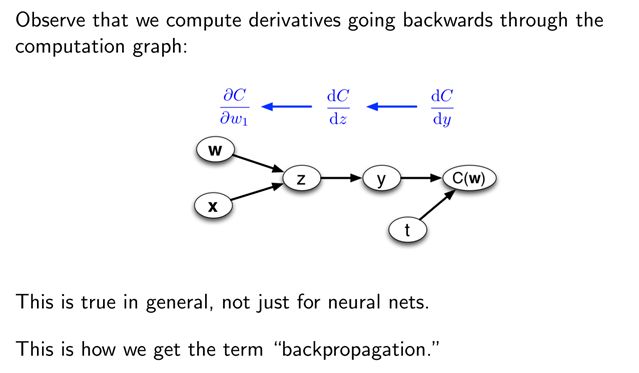
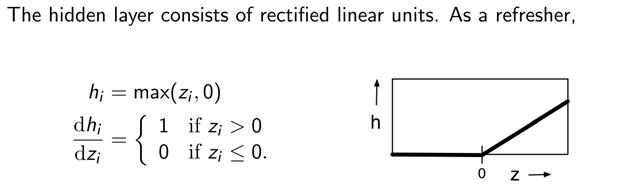
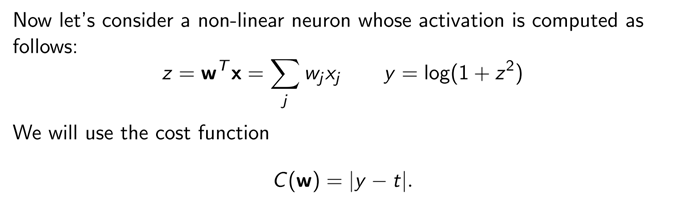- 考虑不可分的例子
-
通过使用basis functions 使得不可分的线性模型变成可分的非线性模型

- 最常用的就是写出一个目标函数 并且使用梯度下降法 来计算
- 梯度的下降法的梯度计算
- 关于线性和非线性的隐层
非线性隐层使得网络可以计算更加复杂的函数
线性隐层不能增强网络的表述能力,它们被用来做降维,减少训练需要的参数数目,这在nlp相关的模型中
经常用到(embedding vector)
- 一个back prop的例子
前向计算 Forward pass
后向计算 Backward pass
激活梯度
权重梯度
来看一下计算某些变量的梯度,需要计算哪些其它变量
另外一些需要了解的
- 许多梯度计算都是0, 这是因为我们采用了线性矫正来作为非线性单元
- 有一些梯度计算出来比其它的大很多,这回造成连乘后传递扩大,这是所谓的"梯度爆炸"
- forward-backward的实例(word2vec)
考虑tensorflow实现的word2vec,tensorflow是可以自动求导的,但是你也可以自己来写这一部分
Word2vec_optimized.py就是自己实现的forward-backward步骤(手写),采用true sgd
看一下代码
# Training nodes.
inc = global_step.assign_add(1)
with tf.control_dependencies([inc]):
train = word2vec.neg_train(
w_in, #上图中左面的w,将在negtrain中被改变
w_out, #上图中右面的w,将在negtrain中被改变
examples, # 中心词编号数组,长度为batch_size
labels, # 周围词 surronding word 编号数组
lr, #学习率 learning rate
vocab_count=opts.vocab_counts.tolist(), #每个词的频次数组
num_negative_samples=opts.num_samples #负样本采样数目
)
REGISTER_OP("NegTrain")
.Input("w_in: Ref(float)") //Ref传递引用
.Input("w_out: Ref(float)")
.Input("examples: int32")
.Input("labels: int32")
.Input("lr: float")
.Attr("vocab_count: list(int)")
.Attr("num_negative_samples: int")
.Doc(R"doc(
Training via negative sampling.
w_in: input word embedding.
w_out: output word embedding.
examples: A vector of word ids.
labels: A vector of word ids.
vocab_count: Count of words in the vocabulary.
num_negative_samples: Number of negative samples per exaple.
)doc");
// Gradient accumulator for v_in.
Tensor buf(DT_FLOAT, TensorShape({dims}));
auto Tbuf = buf.flat<float>();
// Scalar buffer to hold sigmoid(+/- dot).
Tensor g_buf(DT_FLOAT, TensorShape({}));
auto g = g_buf.scalar<float>();
// The following loop needs 2 random 32-bit values per negative
// sample. We reserve 8 values per sample just in case the
// underlying implementation changes.
auto rnd = base_.ReserveSamples32(batch_size * num_samples_ * 8);
random::SimplePhilox srnd(&rnd);
for (int64 i = 0; i < batch_size; ++i) {
const int32 example = Texamples(i);
DCHECK(0 <= example && example < vocab_size) << example;
const int32 label = Tlabels(i);
DCHECK(0 <= label && label < vocab_size) << label;
auto v_in = Tw_in.chip<0>(example);
//正样本label 1, 负样本label -1,累积误差 这里应该是按照MLE 最大化可能概率 所以是累加梯度,参考ng课件
nce的做法,转化为二分类问题
// Positive: example predicts label.
// forward: x = v_in' * v_out
// l = log(sigmoid(x))
// backward: dl/dx = g = sigmoid(-x)
// dl/d(v_in) = (dl/dx)*(dx/d(v_in)) = g * v_out'
// dl/d(v_out) = (dl/dx)*(dx/d(v_out)) = v_in' * g
{
auto v_out = Tw_out.chip<0>(label);
auto dot = (v_in * v_out).sum();
g = (dot.exp() + 1.f).inverse();
Tbuf = v_out * (g() * lr);
v_out += v_in * (g() * lr);
}
// Negative samples:
// forward: x = v_in' * v_sample
// l = log(sigmoid(-x))
// backward: dl/dx = g = -sigmoid(x)
// dl/d(v_in) = g * v_out'
// dl/d(v_out) = v_in' * g
for (int j = 0; j < num_samples_; ++j) {
const int sample = sampler_->Sample(&srnd);
if (sample == label) continue; // Skip.
auto v_sample = Tw_out.chip<0>(sample);
auto dot = (v_in * v_sample).sum();
g = -((-dot).exp() + 1.f).inverse();
Tbuf += v_sample * (g() * lr);
v_sample += v_in * (g() * lr);
}
// Applies the gradient on v_in.
v_in += Tbuf;
}