【学习笔记】ICML2022-GraphBP

一. 代码

Git: https://github.com/divelab/GraphBP

二. 摘要

药物发现的一个基本问题是设计与特定蛋白质结合的分子。为了使用机器学习方法解决这个问题，我们在这里提出了一个名为GraphBP的新颖而有效的框架，通过将特定类型和位置的原子逐个放置在给定的结合位点来生成与给定蛋白质结合的3D分子。特别是，在每个步骤中，我们首先使用3D图形神经网络，从中间上下文信息中获得几何感知和化学信息表示。此类上下文包括给定的绑定位点和放置在前面步骤中的原子。其次，为了保持理想的等方差特性，我们根据设计的辅助分类器选择一个局部参考原子，然后构建一个局部球坐标系。最后，为了放置一个新的原子，我们通过流模型生成其原子类型和相对位置w.r.t.构造的局部坐标系。我们还考虑按顺序生成感兴趣的变量，以捕获它们之间的基本依赖关系。实验表明，我们的GraphBP可以有效地生成具有结合能力的3D分子，以靶向蛋白质结合位点。我们的实现可在https://github.com/divelab/GraphBP上找到

三. 引言

设计可以与特定目标蛋白质结合的分子（又名基于结构的药物设计）是药物发现中一个基本且具有挑战性的问题（Anderson，2003年）。开发解决这个问题的机器学习方法是很有希望的，因为最近有蛋白质-配体复合结构的大规模数据集，例如PDB-bind（Liu等人，2017年）和CrossDocked2020（Francoeur等人，2020年）。此外，机器学习方法已被证明对从生物化学结构丰富的数据中学习是有效的。最有代表性的例子是AlphaFold（Jumper等人，2021年），它从氨基酸序列预测3D蛋白质结构的问题上实现了显著的准确性，这是几十年来的长期挑战。

然而，很少有人探索机器学习方法来生成与特定蛋白质结合位点结合的分子。我们用三个方面总结主要挑战或考虑因素。（i）复杂的有条件信息。在产生能够与特定靶蛋白结合的分子时，3D几何结构和结合位点的化学特征都是重要的考虑因素。考虑如何有效地捕捉这种信息背景至关重要。（ii）巨大的化学空间和连续的3D空间。所有可能的分子的化学空间都是巨大的（估计大于1060），而与特定目标具有结合能力的分子数量非常少。此外，绑定站点周围的3D空间本质上是连续的。换句话说，我们的生成模型最好能够在不离散空间的情况下在任何连续位置生成分子。（iii）等方差性质。直觉上，如果我们旋转或翻译结合位点，生成的分子预计将以同样的方式旋转或翻译。也就是说，我们的机器学习方法产生的分子应该等变于结合位点的任何刚性变换。

在这里，我们介绍了GraphBP，这是一个基于结构的药物设计的新颖而有效的生成框架，它考虑到了所描述的挑战。特别是，我们通过将原子逐个放置到特定的3D结合位点来生成3D分子。在每个步骤中，首先使用3D图神经网络，通过考虑3D几何结构和化学相互作用来提取中间上下文信息。之后，我们根据设计的辅助分类器选择的局部参考原子构建了一个局部坐标系。在这个局部坐标系中生成一个新的原子可以确保等方差性质。最后，为了放置一个新的原子，我们生成其原子类型和相对连续位置w.r.t.，用流模型构造的局部坐标系。此外，感兴趣的变量是按顺序生成的，旨在捕获潜在的依赖项。

据我们所知，在基于结构的药物设计中，我们的GraphBP是第一个满足以下三个特征的机器学习方法；也就是说，它可以感知蛋白质-配体复合物的三维几何结构和化学相互作用，将原子放置在任何连续位置，并保持理想的等方差特性。与之前作品（Ragoza等人，2021年；Luo等人，2021年a）的更多讨论包含在第2节中。实验表明，我们的方法在生成与目标3D蛋白结合位点具有结合亲和力的3D分子方面明显优于基线。

四. 相关工作

1. 1D/2D分子生成

分子可以表示为1D SMILES字符串（Weininger，1988年）或2D分子图。几部作品提议生成SMILES字符串（Gomez-Bombarelli等人，2018年；Kusner等人，2017年；Dai等人，2018年）与序列方法。或者，许多作品通过利用先进的深度生成模型生成二维图。他们要么直接生成节点类型矩阵和邻接矩阵（Simonovsky & Komodakis，2018年；De Cao & Kipf，2018年；Zang & Wang，2020年；Liu等人，2021年b），要么通过逐个添加节点、边缘或图案来生成节点、边缘或图案（Li等人，2018年；You等人，2018年；Jin等人，2018年；Shi等人，2019年；Luo等人，2021年c）。这些方法在不感知3D空间信息的情况下生成1D或2D分子。因此，它们不能直接用于生成用于靶蛋白结合的3D分子。

2. 3D分子生成。

最近，许多作品建议从给定的2D图（Mansimov等人，2019年；Simm和Hernandez-Lobato，2020年；Gogineni等人，2020年；Xu等人，2021年；Shi等人，2021年；Ganea等人，2021年；Luo等人，2021年b），从给定的原子袋（Simm等人，2020年）或从头开始（Gebauer等人，2019年；Hoffmann和Noe ́，2019年；Neserov等人，2020年；Satorras等人，2021年；Luo & Ji，2022年）生成3D分子几何形状。然而，在基于结构的药物设计中，对二维图或原子袋的先前了解是未知的。此外，这些方法通常考虑小有机分子（Luo等人，2021a），因此仍然不足以产生与给定结合位点相互作用的3D类药物分子。为了全面审查分子生成，我们建议参考最近的调查（Du等人，2022年）

3. 基于结构的药物设计

使用机器学习方法生成与特定结合位点的3D分子具有挑战性，探索不足。LiGAN（Ragoza等人，2021年）将蛋白质配体复合物转换为3D原子密度网格，即3D图像。然后，它将基于结构的药物设计视为3D图像生成任务，从而允许使用GAN（Goodfellow等人，2014年）和VAE（Kingma & Welling，2013年）。在生成密度网格后，它执行原子拟合算法来获得3D分子几何形状。作为一项初步工作，它未能保持理想的等方差属性，因为在原子密度网格上执行3D CNN（Ji等人，2012年）不是等变的。此外，它必须离散连续的3D空间来构建网格。最近的另一项工作（Luo等人，2021a）通过建模结合位点周围3D空间中原子发生的分布，然后使用采样算法根据学到的分布放置原子来解决这个问题。在采样过程中，它还将3D空间离散到网格上，并评估原子在网格上发生的概率密度。相比之下，我们的方法可以将原子放置在任何连续位置，从而实现更灵活的原子放置。

4. 自回归流模型

流模型（Dinh等人，2014年；Rezende & Mohamed，2015年；Weng，2018年）定义了一个参数化的可逆变换函数：从潜在空间 $z\sim p_Z$ 中采样获得数据变量x， $f_{\theta }:\mathbf{z}\in$ ${\mathbb{R}}^D\to \mathbf{x}\in {\mathbb{R}}^D$ ，其中pZ是已知的先验分布。数据点x的对数可能性可以通过以下方式计算

log ⁡ p X ( x ) = log ⁡ p Z ( f θ − 1 ( x ) ) + log ⁡ ∣ det ⁡ ∂ f θ − 1 ( x ) ∂ x ∣ \log p_{X}(\boldsymbol{x})=\log p_{Z}\left(f_{\theta}^{-1}(\boldsymbol{x})\right)+\log \left|\operatorname{det} \frac{\partial f_{\theta}^{-1}(\boldsymbol{x})}{\partial \boldsymbol{x}}\right| logpX​(x)=logpZ​(fθ−1​(x))+log ​det∂x∂fθ−1​(x)​ ​ (1)

因此，fθ必须是可逆的，其雅可比行列式应该很容易计算。自回归流模型（Papamakarios等人，2017年）是一种特定的流法，其中变换函数被公式化为自回归模型；也就是说，x的每个维度都取决于之前的维度。形式上，它通常被定义为仿射变换为

${\mathbf{x}}_i={\sigma }_i\left({\mathbf{x}}_{1:i-1}\right)\odot {\mathbf{z}}_i+{\mu }_i\left({\mathbf{x}}_{1:i-1}\right),i=1,\cdots ,D$ (2)

其中标度因子σi(·) 2 R和平移因子μi(·) 2 R是 $x_{1:i-1}$ 的函数。$\bigodot $ 表示按元素乘法。这个变换函数很容易逆，因为 ${\mathbf{z}}_i=\frac{{\mathbf{x}}_i-{\mu }_i}{{\sigma }_i}$ 。此外，雅可比矩阵的行列式可以线性计算，因为它是一个三角形矩阵，具体而言 $\frac{\partial f_{\theta }^{-1}(\mathbf{x})}{\partial \mathbf{x}}={\prod }_{i=1}^D\frac{1}{{\sigma }_i}$

五. 模型框架

0. 符号和问题：

我们将分子（即配体）的三维几何形状表示为 $\mathcal{M}={\left\{\left({\mathbf{a}}_i,{\mathbf{r}}_i\right)\right\}}_{i=1}^n$ 以及蛋白质（即受体）的相应结合位点 $\mathcal{P}={\left\{\left({\mathbf{b}}_j,{\mathbf{s}}_j\right)\right\}}_{j=1}^m$ , n和m分别表示分子和结合位点中的原子数，${\mathbf{a}}_i\in \{0,1{\}}^p$ 是指示分子中第i个原子的原子类型的单热矢量，此外 ${\mathbf{r}}_i\in {\mathbb{R}}^3$ 是它的3D笛卡尔坐标。同样，结合位点中第j个原子的原子类型和坐标表示为 ${\mathbf{b}}_j\in \{0,1{\}}^q$ 和 ${\mathbf{s}}_j\in {\mathbb{R}}^3$ 。 P和q分别表示分子和结合位点中原子类型的总数，它们可以从训练集的统计数据中获得。我们考虑了在给定结合位点生成3D分子的问题。因此，我们的目标是学习一个生成模型，以捕获观察到的蛋白质-配体对的条件分布 $p(\mathcal{M}\mid \mathcal{P})$ 。

图1. GraphBP一代步骤的插图。详情见第3.1节。

1. 分子生成：

1.0 总览

在GraphBP中，我们将给定结合位点中3D分子的生成作为顺序生成过程；也就是说，我们逐个将原子放置到给定的3D结合位点。在第t步，我们根据中间上下文信息C（t-1）生成第t个原子，包括其在和坐标rt处的原子类型。请注意，上下文C（t-1）不仅包含绑定位点，还包含放置在前t − 1步骤中的原子，即 ${\mathcal{C}}^{(t-1)}=$ $\mathcal{P}\cup {\left\{\left({\mathbf{a}}_i,{\mathbf{r}}_i\right)\right\}}_{i=1}^{t-1}$ 。 当t ≥ 2时。在第一步（t = 1），上下文是绑定站点本身 $\text{ i.e., }{\mathcal{C}}^{(0)}=\mathcal{P}$ 。

在每个步骤中，我们首先根据上下文生成原子类型。之后，通过考虑上下文和生成的原子类型信息来生成其坐标。因此，我们生成过程的每个步骤 $t(t=1；2；\cdot \cdot \cdot \cdot ；n)$ 都可以表述为

$\begin{array}{l}{\mathbf{a}}_t=g^a\left({\mathcal{C}}^{(t-1)};{\mathbf{z}}_t^a\right)\\ {\mathbf{r}}_t=g^r\left({\mathcal{C}}^{(t-1)},{\mathbf{a}}_t;{\mathbf{z}}_t^r\right)\\ {\mathcal{C}}^{(t)}\leftarrow {\mathcal{C}}^{(t-1)}\cup \left\{\left({\mathbf{a}}_t,{\mathbf{r}}_t\right)\right\}\end{array}$

生成器 $g^a$ 和 $g^r$ 是自回归函数。 $z_t^a$ 和 $z_t^r$ 表示步骤t时流模型中使用的潜在变量，这些变量将在稍后详细介绍。

在下面，我们描述了一代步骤的细节，即自回归函数 $g^a$ 和 $g^r$ 是如何参数化的。此外，我们还解释了GraphBP如何考虑第1节中总结的关键挑战。特别是，一个生成步骤中主要有三个部分，即编码上下文、选择局部参考原子和放置新原子，如图1所示。细节阐明如下。

1.1 编码上下文

1.2 选择本地参考原子

1.3 放置一个新原子

1.4 整体生成过程

2. 训练

为了训练我们的自回归生成模型，我们需要将配体-蛋白质对中的3D分子分解为原子放置步骤的轨迹。受G-SphereNet（Luo & Ji，2022）的启发，我们预计新原子在生成过程中应放置在参考原子的局部区域。因此，我们选择结合位点中离配体最近的原子作为第一个局部参考原子，即接触原子，将配体中离结合位点最近的原子作为第一个生成的原子。然后，从配体中的这个选定原子开始，我们将Prim算法应用于3D分子几何，以获得配体中原子的放置顺序及其相应的局部参考原子。该策略可以保证每个步骤的新原子始终位于相应参考原子的局部区域。通过这种获得的轨迹，GraphBP通过随机梯度下降使用以下三个损失函数进行训练。

2.1 原子放置损失

2.2 相联原子分类器损失

2.3 中心原子分类器损失

六. 实验

我们首先评估我们的GraphBP生成能够与给定蛋白质靶点结合的3D分子的能力。实验表明，GraphBP的表现显著优于基线。之后，我们进行消融研究，以验证第3.1.3节中提议的顺序生成的有效性。

1. 数据集

我们使用CrossDocked2020数据集（Francoeur等人，2020年），其中包含超过2200万个对接蛋白配体晶体结构，来评估GraphBP的基于结构的药物设计。在LiGAN（Ragoza等人，2021年）之后，我们忽略了任何根均方偏差（RMSD）大于2A的姿势，从而获得具有约50万蛋白配体复合物的数据集̊。我们使用与LiGAN相同的训练集和测试集，以进行公平比较。配体和结合位点中的原子类型总数分别为27种和19种。原子类型汇总于附录B

2. 设置

我们使用与LiGAN相同的10种目标蛋白质进行测试评估。它们中的每个都可以有多个相关的配体，导致测试集中有90个蛋白质配体对作为参考。根据LiGAN，我们为测试集中的每个参考结合位点生成100个带有GraphBP的分子。这种评估设置具有挑战性，因为测试目标从不同的袖珍集群中选择多种多样，参考配体通常与目标绑定位点紧密结合（Ragoza等人，2021年）。我们通过两个指标定量测量生成性能：（i）有效性是所有生成分子中化学上有效的分子的百分比。如果一个分子可以被RDkit消毒，它就是有效的（Landrum等人，2006年）。（ii）∆结合测量比相应的参考分子具有更高预测结合亲和力的生成分子的百分比。请注意，我们无法进行湿实验室实验分析来评估生成分子的结合亲和力。此外，没有可以作为评估绑定亲和力的黄金标准的计算指标。因此，继LiGAN之后，结合亲和力是由在CrossDocked2020数据集上训练的CNN评分函数（Ragoza等人，2017年）预测的。事实证明，这种CNN预测的亲和力比使用Autodock Vina经验评分功能更准确（Trott & Olson，2010年）。因此，它可以作为评估生成分子结合亲和力的合理和令人信服的指标。在LiGAN之后，我们首先通过通用力场最小化（Rappe等人）来细化生成的3D分子。，1992年）。之后，通过使用分子对接程序gnina将Vina最小化和CNN评分应用于生成的分子和参考分子（McNutt等人，2021年）。

3. 基线

我们认为最近LiGAN（Ragoza等人，2021年）方法的两个变体作为基线。LiGANprior在给定的结合位点上生成条件分子，其条件信息与我们的GraphBP相同。LiGAN-posterior将整个参考蛋白质配体复合物编码为条件信息，从而产生偏向参考分子的分子。请注意，LiGAN-posterior比GraphBP和LiGAN-prior包含更多的条件信息

4. 结果

我们在表1中列出了定量结果。我们的GraphBP可以产生比基线更多的有效分子，包括LiGAN后验分子，LiGAN后方甚至包括有效的参考配体作为条件信息。更重要的是，GraphBP生成的分子中有27:0%的预测结合亲和力高于参考分子。这以11:1%的绝对优势优于LiGAN。这些比基线的重大改进表明，结合了图表示和更灵活的原子放置策略的GraphBP可以更有效地捕获结合位点条件的3D分子几何的基本分布

我们在图2中进一步提供了∆Binding亲和力的详细分布。请注意，LiGAN-posterior的平均∆Binding亲和力高于LiGAN-prior和GraphBP，但方差更低。这表明LiGANposterior将参考分子编码为条件，可能会对参考分子进行轻微修改。尽管与LiGAN-posterior相比，我们的GraphBP仍然产生比参考分子更强的分子（27:0%对15:4%），这表明GraphBP可以通过有效捕获潜在的条件分布来产生更多样化的分子来与目标蛋白质结合

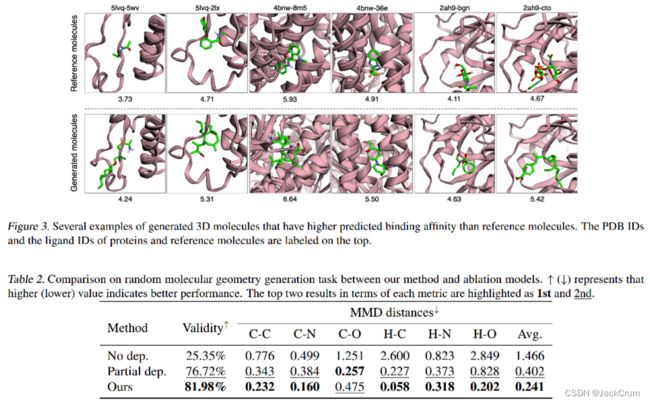
在图3中，我们提供了几个生成的3D分子的例子，这些3D分子预计将比其相应的参考分子更强烈地与目标蛋白质结合。可以观察到，我们生成的具有更高预测结合亲和力的分子与参考分子大不相同，这进一步表明我们的模型能够产生多样化和新颖的分子来结合目标蛋白质，而不仅仅是记忆或修改已知分子

5. 消融实验

在第3.1.3节中，我们建议按顺序生成感兴趣的变量，以捕获其基本依赖项。具体来说，给定上下文C(t−1)，我们以C(t−1)的形式生成at、dt、θt和’t一个接一个！在！Dt！Θt！'T。为了验证该策略的有效性，我们采用了以下两种变体。（i）没有依赖性。at、dt、θt和’t的变量独立于上下文生成，如C(t−1)！在，C（t-1）！dt，C（t-1）！θt和C（t−1）！'T。因此，我们省略了原子类型嵌入（Eq.（12））、距离嵌入（Eq.（14））和距离角嵌入（Eq.（16））。（ii）部分依赖。在生成dt、θt和’t时，我们会考虑生成的原子类型信息。然而，dt、θt和’t是独立处理的。它可以表示为C（t-1）！在，（C（t-1）；在）！dt，（C（t-1）；at）！θt和（C（t−1）；at）！不会，导致与GSphereNet类似的模型（Luo和Ji，2022年）。为了提高效率，我们选择进行随机分子几何生成实验，避免编码大型结合位点。根据G-SphereNet，我们训练QM9的3D分子模型（Ramakrishnan等人，2014年），并评估生成的分子几何形状。评估指标是生成分子的有效性和生成的3D分子和训练3D分子之间键长分布的最大平均差异（MMD）（Gretton等人，2012年）。图5附录C说明了不同模型和训练分子产生的分子的键长分布。

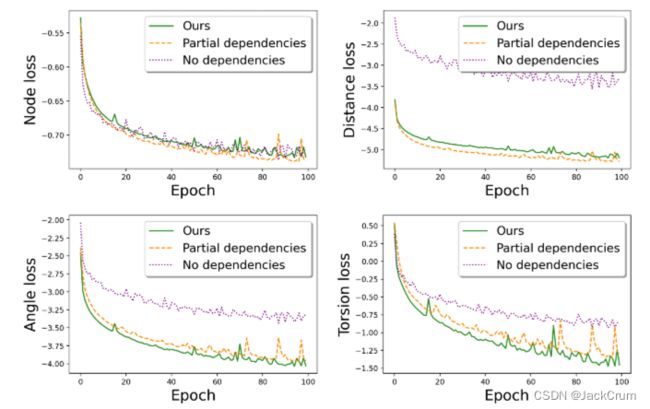
表2总结了比较情况。它表明，添加依赖项可以持续提高生成性能。我们的顺序生成方法表现最佳，证明它可以通过捕获变量之间的潜在依赖关系来更有效地模拟分子几何分布。由于原子放置的损失（等式（18））可以分别分为w.r.t.原子类型、距离、角度和扭转的损失，我们可以通过观察这些变量相应的训练损失来进一步分析它们的建模能力。我们在图4中说明了训练损失的比较。通过观察每个变量的损失，我们可以得出结论，添加依赖项有助于更好地适应训练数据

七. 结论

在这项工作中，我们提出了GraphBP，一种机器学习方法，用于生成用于靶蛋白结合的3D分子。GraphBP能够捕获蛋白质-配体复合物的3D几何结构和化学相互作用，在不离散3D空间的情况下放置原子，并在生成过程中保持等方差特性。GraphBP被证明是有效的，在生成与目标蛋白质紧密结合的3D分子方面明显优于最近的基线。

图4。我们的方法和消融模型之间训练损失的比较