【深度学习】——深度学习中基本的网络结构(1)
优质资源分享
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| Python实战微信订餐小程序 | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| Python量化交易实战 | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
这一部分开始,是对深度学习的有关内容进行学习,在机器学习中有涉及到部分有关深度学习的内容,如CNN、autoencoder等比较简单的网络模型。这一部分开始,将对深度学习有一个较为系统的学习和了解。
除了基本理论内容外,中间可能穿插一些tensorflow来实现一些东西,也将在这里一并涉及。
深度学习中常见的网络结构
0.前言
机器学习中有一个通用的三步走的策略:1.function set 2. cost function 3. find the best model。而在深度学习中同样也是通用的:
第一步:设计一个网络结构,网络结构的参数的不同,组成了一系列的function set,通常深度学习中需要我们自己去设计出网络的结构,然后让其自动学习其中的参数;
第二步:设计损失函数,通常损失函数根据任务不同需要设计不同的损失函数;
第三步:根据损失函数,让机器自己去学习得到所设计网络中的各个参数。
本节主要介绍一些在深度学习中常见的一些网络结构,当然,网络结构是多种多样的,也不可能罗列和学习的完,这里主要一些常见的或者说是主流的一些结构进行介绍,包括:
-
全连接网络结构
-
Basic RNN
-
RNN中的LSTM
1.全连接网络结构(fully-conneced)
这种网络结构在机器学习中做了初步的介绍,在前面介绍时,都是以“元素化”的形式进行计算,而在深度学习中多以矩阵的形式运算,在此先对结构中的变量进行声明:
首先,对于某一层而言:
ail表示第l层的第i个元素,上标“l”表示第l层隐藏层,下标“i”表示第l层的第i个神经元。那么al则就表示一个向量。
接下来就是全连接中的运算:
从l-1层到第l的运算,第l层的每一个元素都与第l-1层每一个元素有关,因此称之为全连接网络。
而连接ail与ajl-1的边称之为权重wijl,那么整个w就可以写成矩阵的形式,矩阵的行数是第l层的神经元的个数,矩阵的列数则是第l-1层的神经元个数。
同样地,对于参数b,也是一样:
第l-1层的输出al-1经过w和b的转换后,再经过激活函数,可以得到al,在经过激活函数前,变量为z,那么:
那么从第l-1层到第l层的全连接网络的运算表示为:
然后zl再经过激活函数:
这样就以矩阵的形式表示出在全连接网络中两层之间的关系了:
以上就是全连接网络的基本形式和计算过程。
2.RNN
RNN(Recurrent Neural NetWork)是深度学习中最常见也是最常用的一种技术。为什么要用RNN呢?
假设在slot filling中,有一个订票系统,一个人说:
在这句话中**"Taipei"表示目的地**,出发时间是11月2日。
如果用传统的神经网络来自动识别出目的地和出发日期,我们训练一个网络:
输入“Taipei”则对应的输出在目的地的概率大,相反,在出发日期的对应的y的概率大。
然而,这里会有一个问题,当另一个人说了一句话:
而此时的**"Taipei"变成了出发地**,时间变成了出发时间,但对于传统的网络来说,同样的输入"Taipei"则对于模型而言就无法分出是出发地还是目的地。
此时传统的网络模型就失效了。
此时就要用到RNN了,之所以RNN可以奏效,是因为RNN可以存储之前的信息,通过上下文再进行决策。RNN是如何存储信息的呢?
RNN的基本结构图下:
可以看到,相比于传统的神经网络,多了cell,可以用来存储信息,这些信息来自于之前的输入。
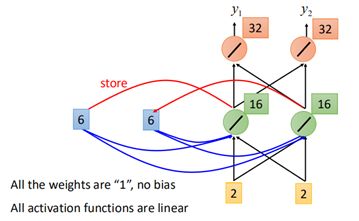
如何存储呢?下面举个例子,假设有三组数据:
网络所有的权重假设为1,初始化cell都为0,那么当输入【1,1】时,第一个layer输出为【2,2】,那么【2,2】被存储到cell中,再经过下一个layer,输出为【4,4】。
然后下一个时刻,这个存储到cell中的值就会被拿来当做输入,并和该时刻的x一起输入到第一个layer中去:
然后经过后面的结构,第二个时刻输出为【12,12】。此时cell存储的值也被更新为【6,6】。
依次类推,到第三个时刻,输入【2,2】,那么cell中的【6,6】将一起作为输入到网络中:
最终输出为【32,32】。
而当输入的顺序改变时,那么输出也就不同。因此对于相同的输入,由于上下文不同以及输入的顺序不同,RNN的输出也就不同。
上面就是RNN的"前向传播"的过程,RNN是随着时间进行传播的,将前面时刻的输入保留“记忆”,输入到下一个时刻中,总的来说,RNN的基本结构如下:
由于训练时“Taipei”前面的输入不同,因此,对于输出也是不同的:
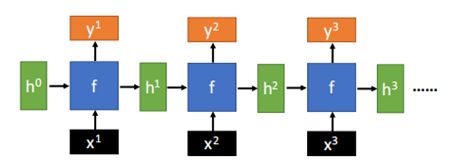
那么RNN的一般架构如下:
其中f是一种网络结构,且这种结构在RNN中被反复使用,也就是说,其中的参数都是一致的。
当然RNN也可以是Deep的:
还有一种比较常见的RNN结构,是双向RNN:
也就是说,对于yt而言,不仅仅只由xt来决定,还有xt+1,xt+2…决定。
以上就是一般的RNN的几种基本结构,之所以称之为最基本的结构,是因为其中的网络结构是最基本的,也就是:
这种结构通过输入x和前一个时刻的输出h,决定当前时刻的输出y。f的组成就是一堆普通的neural组成的。
然而,RNN也存在一定的问题,当输入的序列很大时,假设一个最简单的RNN:
那么:
可以看到,由于长期的依赖问题,当序列长度过长时,w有略微增大时,最终输出的结果就变得很大,此时梯度极大,产生梯度爆炸;
当w微小变化时,则输出变为0,此时梯度几乎也为0,产生梯度消失。
而为了解决这种长期依赖导致梯度消失的问题,LSTM也就应运而生。
3. LSTM
LSTM(Long Short-term Memory)是一种解决RNN长期依赖导致的梯度消失(不是梯度爆炸)的方法,先来说LSTM的基本结构,然后再说为什么可以解决梯度消失。
一个LSTM的基本单元结构如下:
这个单元有3个gate和一个memory cell,gate负责控制memory的通路;
输入有四个:
1、一个输入x(这个x是经过一个转换后的);
2、一个控制input gate的信号,该信号决定x是否要写进memory;
3、一个控制forget gate的信号,该信号决定着memory里的内容是否要被重置;
4、一个控制output gate的信号,该信号决定着memory里的内容是否要被输出。
输出有一个:
单元的输出。
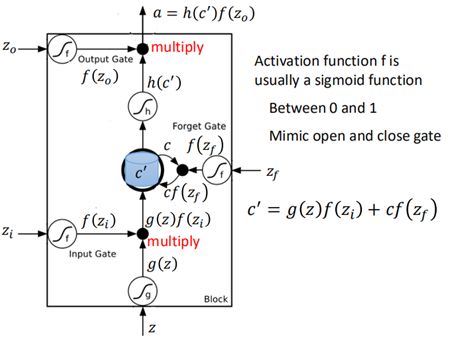
更具体地,LSTM的基本单元结构为:
在LSTM结构里这几个门的激活函数f通常使用sigmoid函数,这是因为sigmoid输出值在0~1之间便于控制门的开启和关闭。
该结构中,输入为z(输入)、zi(操控input gate的信号)、zo(操控output gate的信号)、zf(操控forget gate的信号):
1、z经过激活函数g,得到g(z);
2、zi经过激活函数f,得到f(zi);
3、g(z)与f(zi)相乘(element wise),得到节点处的值;此时,如果input gate被关闭,f(zi)=0,二者相乘也为0,所以输入z不会被考虑。
4、zf经过激活函数f,得到f(zf);
5、f(zf)与原cell中的c相乘,再与节点处的值相加,得到新的c’;此时如果f(zf)为0,也就是forget gate被关闭时,则原cell中的c就会被遗忘;
6、新的c’存入到cell中去;
7、c’经过激活函数h,得到h(c’);
8、zo经过激活函数得到f(zo),然后与h(c’)相乘,得到输出,当f(zo)为0时,也就是output gate被关闭时,则输出为0;
上面就是单个cell进入LSTM单元的计算过程,那么当有多个cell时,组成一个向量:
综上,为了更加清晰地描述LSTM的结构,全部采用向量的形式:
然后zf,zi,z,zo在LSTM的结构中进行运算:
有时也会把上一个时刻的ct-1一并放入到z的计算当中去,称为peephole:
通常将ct-1放入时,w矩阵对应的ct-1那一块一般会强制为对角矩阵(一般规定这么做,也确实有好的结果,至于为什么…)。
当然,上面只是一个时刻的,下一时刻同样地:
以上就是LSTM的基本结构,那么之所有LSTM可以解决梯度消失的问题,主要有两个原因:
1、LSTM的memory不单单是序列之间传递时相乘的,还有一部分是相加的;
2、LSTM的memory一直都不会消失,除非当forget gate被关闭时,才会被洗掉。
上面就是LSTM的基本结构和前向传播过程。
上边LSTM有3个gate,还有另外一种结构, 可以说是LSTM的进阶版,叫做GRU,其结构如下:
不同于LSTM的是,GRU只有input gate和forget gate,而且两个gate是相互联动的,input gate打开时,forget gate就会被关闭。
这样GRU相当于在LSTM的基础上又减少了参数,比较不容易过拟合。
4. CNN
卷积神经网络(CNN)在【机器学习基础】部分已详细学习过了,这里就不再写了。
5. RNN的应用
RNN根据任务的不同,输入输出也就不同,对于不同的输入和输出的序列长度,在设计RNN网络结构时也存在差异,一般有如下几种情况(图片来源于网络):
对于many2one,在语义分析或者评论文本分析中经常用到:
而对于many2many使用场景比较广泛,比如翻译、语音识别等都是这样的情况,而在many2many也分为输入输出相等、输出更短、无限制的情况。
对于输入输出同等长度的就不再说了,下面看下输出更短的情况,在语音识别中:
通过输入声音信号处理后的特征(acoustic features),转换为输入输出同等长度,然后再去掉重复的字就可以了。
但是这样无法处理叠词的问题,“好棒”和“好棒棒”两个相反的词义,就无法进行分辨。一种处理这种情况的方法就是CTC(Connectionist Temporal Classificaion)。
CTC通过添加特殊符号**“φ”**来处理叠词的问题:
这样就解决这个问题了,那么带有“φ”的符号在训练时,就要穷举每个可能的符号是“φ”的情况,认为这些都是正确的样本:
而对于另一个many2many没有限制输入输出数量的问题,比如翻译:
训练时需要在句子的末尾加上结束的标志:
对于没有标签的学习任务,比如文本语义的分析,对于组成相同的两句话:
两句话的意义却完全不同,此时使用前面说过的autoencoder可以解决这样的问题:
autoencoder也可以用于语音识别中,比如听歌识曲,将歌曲用一code来表示,输入一段歌曲,可以搜索相近的code进行匹配:
上面就是在深度学习中一些基本的网络结构,随着深度学习的发展,这些结构也出现了各种各样的形式,但万变不离其宗,这部分是后面学习的基础,后面学习到再进行完善和补充,接下来就复习一下这些基本的结构在tensorflow中的实现。