对称加密算法:DES
注意:本文首发于我的博客,如需转载,请注明出处!
Feistel结构设计
流密码与分组密码
在最开始,我们有必要了解一下流密码和分组密码。对于明文 m m m,我们有两种加密方式,一种是逐位加密,我们称这种加密方式为流密码;另一种方式是按照一定的长度作为一组一同加密,这样的加密方式称为分组密码。流密码的典型例子是凯撒密码,它就是对明文逐位加密的。相较于流密码,我们实际应用中更偏向于使用分组密码,因为流密码有一个缺陷:如果密钥长度不足,那么字符的统计规律就难以被隐藏,很容易受到基于统计的攻击。分组密码在一定程度上会更多地抹去统计信息,因此也就显得更安全。我们主要讨论分组密码。
Feistel密码结构的设计动机
我们不妨假设分组密码作用在长度为 n n n的明文分组上,相应地,我们得到相同长度的密文。我们假设明文信息流是二进制流,那么长度为 n n n的分组至多有 2 n 2^n 2n中情况。考虑到我们需要从密文复原到明文,因此,我们选择的分组替代方式应该是单射的。我们称这样的变换为可逆变换,也叫非奇异变换。上述例子中,非奇异变换一共有 2 n ! 2^n! 2n!种 (注:对于第一个分组,我们可以从 2 n 2^n 2n中选取一个映射;对于第二个,有 2 n − 1 2^n-1 2n−1种;以此类推)。这种加密方式下,映射表格就是密钥。这样看来,我们具有很大的密钥空间,任意一种分组情况选取的映射是任意的。我们称这种加解密映射为任意可逆变换。Feistel称这种密码为理想分组密码,因为它允许生成最大数量的加密映射来映射明文分组。
然而,这种方法是难以应用的。如果我们分组的 n n n的值不够大(例如4),那它就和流密码没什么区别,非常容易基于统计规律被攻破;那 n n n很大的情况呢?统计规律固然被隐藏了,但是我们提过一句话:映射表格就是我们的密钥。对于分组长度为 n n n的任意可逆变换,其每种映射需要 n n n位表示(即分组长度),并且我们有 2 n 2^n 2n中不同分组情况,因此,密钥长度可以表示为
L ( n ) = n ⋅ 2 n . L(n)=n\cdot 2^n. L(n)=n⋅2n.
指数级的增长是十分恐怖的。今天的密钥长度一般不少于64位,如果我们令上式中的 n = 64 n=64 n=64,其结果是 1 0 21 10^{21} 1021位!这个长度是不可接受的。因此,Feistel指出,我们只需要一种对任意可逆变换的近似。一般我们认为密钥空间是上面所提到的 2 n ! 2^n! 2n!中的一个子集。于是,我们依靠什么标准来选取这个密钥空间使得其在降低密钥空间大小的情况下依然能保持足够的安全呢?
Feistel的设想
Feistel提出了一种基于乘积密码的概念来逼近任意可逆变换的方式。乘积密码是说,利用不同的两套或多套密码来加密,得到的结果比其中任意一种的加密效果都要强。特别的,Feistel建议使用替代和置换的反复使用。替代是指明文中的某一元素或某一组被唯一地替换成为密文中的某一元素或某一组;置换是改变明文元素顺序,但明文元素本身并不发生改变。这样的目的是产生混淆和扩散,这是香农提出的概念。其大致原理是,使得密文中的某一字符尽可能多地受到来自不同明文字符的影响,这样做可以有效抵御基于统计的密码分析。当然,最好的情况是所有统计规律都独立于密钥的选取,但这就是我们前面说的任意可逆变换,是不能够实际应用的。排除这种可能,由于密文的生成是明文和密钥的函数,因此,密文的统计规律不可避免出现密钥的信息。因此,大量使用替代和置换可以使这种关系变得复杂,挫败密码分析,这就是我们要的结果。
Feistel结构的基本特征
分组长度:不言而喻的,分组长度越大,密码的安全性就越高。正如前面分析的那样,这种安全性来源于混淆和扩散。一般的分组长度是64-bit,高级加密标准下是128-bit。
密钥长度:密钥越长安全性也显而易见的越高。但是这种安全性建立在牺牲了加解密速度之上。现代密码学中我们认为64-bit的密钥还不够,一般选取128-bit。
迭代轮数:迭代轮数是降低统计特征的最好方式。一般的推荐迭代轮数是16。
子密钥产生算法:我们在前面说过,我们要使用的是乘积密码的原理,因此,如何生成每一步的密钥是关键的问题。产生密钥的算法越复杂,安全性就越高。
轮函数 F F F:轮函数是明文和密钥的函数。同样的,轮函数越复杂,密码安全性越高。
快速加解密:对称密码的优势之一就是速度快。作为对称加密算法的Feistel结构,也应当保持这样的优势。
简化分析难度:尽管我们喜欢把算法设计得尽可能使密码分析变得困难,然而将算法设计得易于分析也有它的好处。如果说算法被描述得简单一些,我们就更容易分析出其脆弱性,进而设计更可靠的加密算法。不过,我们后续要介绍的DES并没有简单的分析方式。
Feistel加密算法
本节介绍Feistel加密算法,其大致原理可以用下面的图来直观表示。当然我们也会对整个流程做出解释。
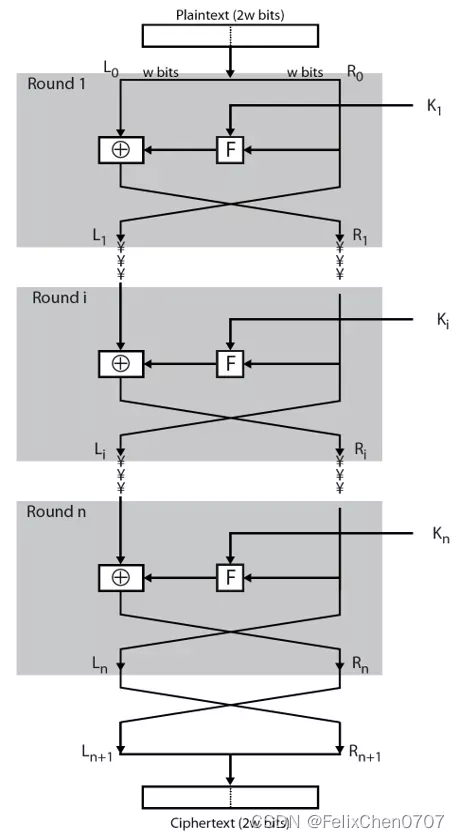
不妨假设我们的明文输入是 2 w 2w 2w位的。我们先对其分组,分成两部分,每一个部分是 w w w位长的,并且将它们分别记作 L E 0 LE_0 LE0和 R E 0 RE_0 RE0。我们对这个明文进行第一次迭代。我们如何获取 L E 1 LE_1 LE1呢?很简单,我们直接将输入数据的右半部分拷贝过来即可,即
L E 1 = R E 0 . LE_1=RE_0. LE1=RE0.
比较复杂的是 R E 1 RE_1 RE1的获得。
我们先选取明文的右半部分 R E 0 RE_0 RE0,对其作用轮函数 F F F,密钥选择第一把子密钥,即这部分的运算结果是
F ( R E 0 , K 1 ) . F(RE_0,K_1). F(RE0,K1).
我们将上述得到的式子和 L E 0 LE_0 LE0作异或运算,于是得到我们需要的 R E 1 RE_1 RE1,这个过程用数学表达式表示就是
R E 1 = L E 0 ⊕ F ( R E 0 , K 1 ) . RE_1=LE_0\oplus F(RE_0,K_1). RE1=LE0⊕F(RE0,K1).
这就是第一轮迭代的结果。我们将这个迭代再重复15次,即一共迭代16次,最终得到 L E 16 LE_{16} LE16和 R E 16 RE_{16} RE16。上面式子用一般地表示方法即为
L E i = R E i − 1 , LE_i=RE_{i-1}, LEi=REi−1,
R E i = L E i − 1 ⊕ F ( R E i − 1 , K i ) . RE_i=LE_{i-1}\oplus F(RE_{i-1},K_{i}). REi=LEi−1⊕F(REi−1,Ki).
当我们得到 L E 16 LE_{16} LE16和 R E 16 RE_{16} RE16后,我们对这两部分作最后一次交换,得到
L E 17 = R E 16 , LE_{17}=RE_{16}, LE17=RE16,
R E 17 = L E 16 , RE_{17}=LE_{16}, RE17=LE16,
于是, L E 17 R E 17 LE_{17}RE_{17} LE17RE17就是我们产生的密文。
这就是Feistel结构的加密过程。
Feistel解密算法
既然其加密算法看上去这么复杂,其解密算法会不会也很复杂呢?答案是并不是。其解密算法和加密算法完全一致,除了使用密钥的顺序和加密过程相反。这样究竟能不能复原出明文,这是我们关心的问题,下面我们给出证明。
我们要知道的是, L E i LE_i LEi和 R E i RE_i REi在我们知道密钥 K i K_i Ki的情况下能不能反解出 L E i − 1 LE_{i-1} LEi−1和 R E i − 1 RE_{i-1} REi−1。我们由式(4)可以知道
L E i − 1 = R E i ⊕ F ( R E i − 1 , K i ) , LE_{i-1}=RE_i\oplus F(RE_{i-1},K_i), LEi−1=REi⊕F(REi−1,Ki),
又由于 R E i − 1 = L E i RE_{i-1}=LE_i REi−1=LEi,有
L E i − 1 = R E i ⊕ F ( L E i , K i ) . LE_{i-1}=RE_i\oplus F(LE_i,K_i). LEi−1=REi⊕F(LEi,Ki).
又显然有
R E i − 1 = L E i , RE_{i-1}=LE_i, REi−1=LEi,
也就是说,我们获得了密文后,便可以一层层代入解密。至于在加密过程中为什么要增加一步互换位置,是因为互换以后我们得到的密文中的右半部分
R D 0 = R E 17 = L E 16 , RD_0=RE_{17}=LE_{16}, RD0=RE17=LE16,
这样,我们在解密过程中可以保持对右半部分使用轮函数,保证了加密解密算法的一致。
值得注意的是,上述论证过程中我们并没有假设轮函数具有什么性质,因为事实上,轮函数是可以任意选取的,这不影响我们的解密过程。我们后面要讲述的DES,实际上是Feistel结构的一个具体实现。
DES加密算法
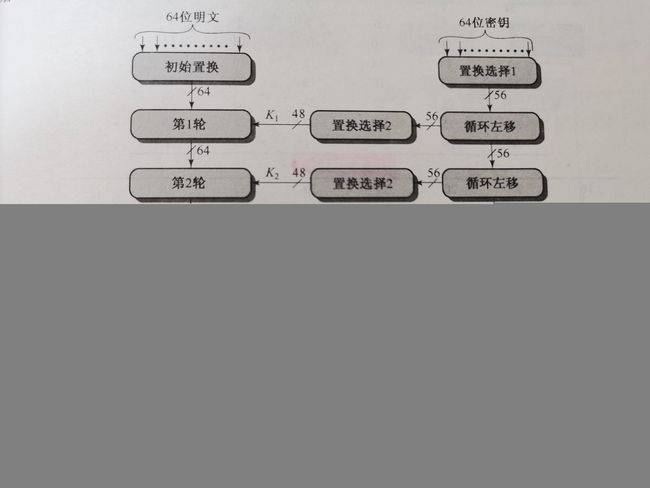
DES加密算法以64位为分组,密钥长度为56位 (实际上,使用的密钥为64位,但是其中8位是校验位,不参与实际运算,因此说是56位)。加密的粗糙流程可见下图。
我们获取到明文输入后,首先对其进行初始置换( I P IP IP),然后经过16轮迭代,最后经过左右互换(这点在Feistel结构中提到过),然后通过逆初始置换( I P − 1 IP^{-1} IP−1),得到密文输出。初始置换和逆初始置换是一对互逆运算。笔者认为其存在的意义仅仅是增加解密复杂度。每一轮加密的密钥来源于64位初始密钥生成的子密钥。以下我们解释一下DES的详细加密过程。
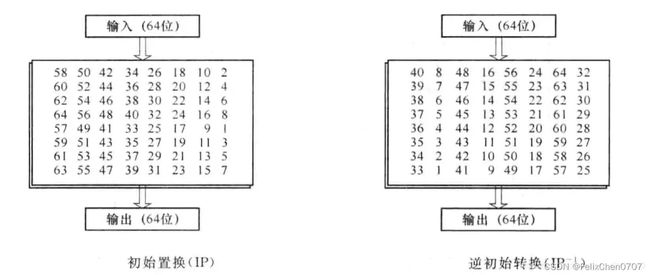
初始置换
初始置换和逆初始置换只在最开始和结束使用,其原理是地址置换,即将对应位置所指的地址的数据置换到该位上。下面给出了具体的初始置换和逆初始置换表。这里不多赘述。
轮函数的细节
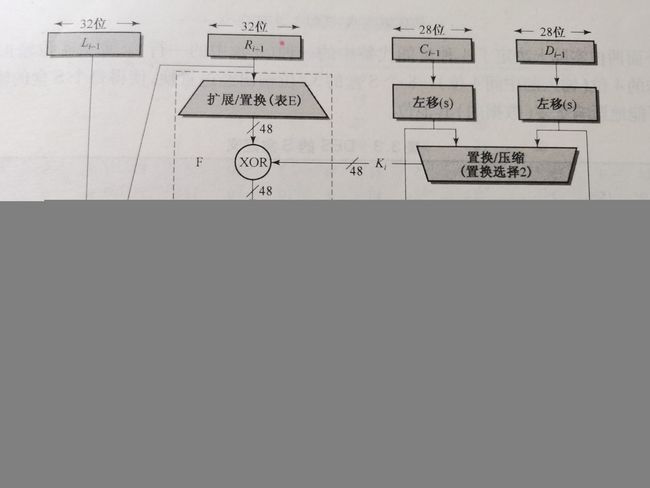
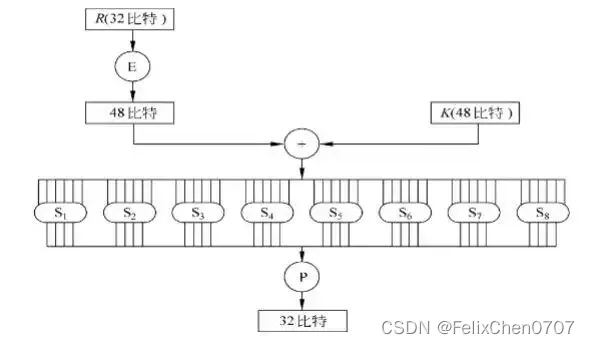
我们先给出轮函数的示意图,然后再解释。
如同我们在Feistel结构中提到的,我们对64位明文信息分组称为左右两部分。由图上可知,轮函数外的步骤和Feistel结构完全一致,我们不多赘述。关键来看一下轮函数中的最重要的四步:E扩展置换,子密钥运算,S盒压缩和P置换。
E扩展置换
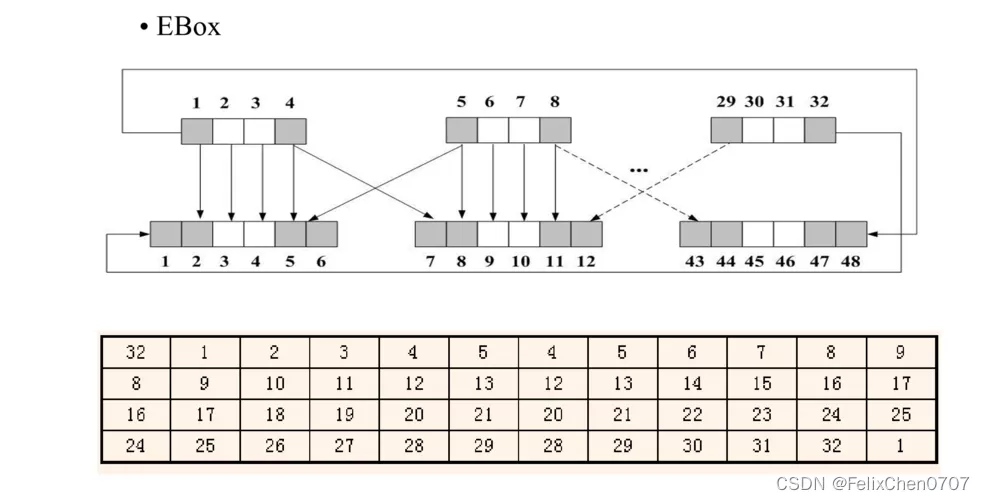
由于参加运算的子密钥是48位的,然而分组后我们的明文信息只有32位,因此,需要对明文信息扩展称为48位。E扩展是有对应表格的,它接受32位的输入,产生48位的输出。具体的扩展方式可以见下面的表格和例子。这样的扩展会产生16个重复的位。
子密钥运算
将扩展置换结果与子密钥进行与或运算。
S盒压缩
上述的运算结果是48位的,然而,轮函数迭代后的位数是不能够增多的。因此,我们需要对48位的数据压缩,将之长度还原到32位。S盒压缩就是在完成这一步。**S盒压缩接受48位的输入,产生32位的输出。**其原理如下图。
S盒首先将输入分成6位一组,共计8组。我们不妨假设输入是011001。首先我们获取输入的首尾两位,将其作为行号;剩余的四位作为列号。在上面的例子中,行号是1(01);列号是12(1100)。我们查询S盒置换表,知道这一位数字是9,即1001。于是,1001就是我们的输出。对于其他7组也是如此,最后一共输出8组4位,共32位的结果。值得注意的是,S盒不止一个。其设计标准是不公开的,但S盒是公开的。
P置换
也是一种简单的置换,具有置换对照表。
子密钥的生成
我们输入的是64位的密钥。于是我们通过PC-1置换,将密钥的校验位去除,同时打乱密钥的顺序,得到56位的密钥。对这个56位密钥我们再次进行分组,分为左右两半部分各28位长度的密钥。我们把这个密钥称为 C 0 D 0 C_0D_0 C0D0。我们对其两部分分别进行左移,左移位数查表可见。对于每一次的左移结果,我们通过PC-2置换得到该次加密的子密钥。重复上述操作,我们可以得到所有加密过程需要的子密钥。
DES密码的强度
对于P置换和S盒压缩是有要求的,就是要尽可能增加其中某一位对其他所有位变化的敏感度,也就是说,增加算法的扩散程度,来弥补分组算法本身难以逃脱统计攻击的特点。因此,不论是置换表格的设计,又或是子密钥的生成,都要严格遵循一个效应,我们称之为雪崩效应。雪崩效应说的是,明文或密钥的微小改变将对密文产生很大的影响,换句话说,明文和密钥的任何一位的改变会导致密文很多位的改变。这样,分析者搜索密钥的难度大大上升,加密算法也更加健壮。
但,DES密码并不是牢不可破的。其安全性一直备受质疑。曾在1998年,有一台专门针对DES加密算法的计算机成功破译了DES加密算法。但实际上,这种破译往往需要我们知道待破译的目标语言特点,例如语言特征,文件格式等等。因此,在不知道这些信息的情况下,破译DES依然是有难度的。不论如何,我们如今也有许多DES的替代加密方案例如AES和3DES。对这些方案,我们后续也会加以讨论。
不论如何,Feistel结构和DES加密算法仍旧是对称加密算法中的经典,理解它们对我们后续的深入学习是有百利而无一害的。