混淆矩阵与miou代码
一、混淆矩阵
# 计算混淆矩阵
def generate_matrix(num_class,gt_image, pre_image):
#正确的gt_mask
mask = (gt_image >= 0) & (gt_image < num_class) # ground truth中所有正确(值在[0, classe_num])的像素label的mask
#gt_image[mask] 和 pre_image[mask]是一维数据
label = num_class * gt_image[mask].astype('int') + pre_image[mask]
# np.bincount计算了从0到n**2-1这n**2个数中每个数出现的次数,返回值形状(n, n)
count = np.bincount(label, minlength=num_class ** 2)
confusion_matrix = count.reshape(num_class, num_class) # 一维到(n,n)
return confusion_matrix上面label是重点,它计算了在一维中对应于二维混淆矩阵中的位置。
在一维数据中 n * gt_class + pre_class 对应了二维矩阵中的 位置
eg:
ground truth和预测
pre = np.array([[0, 0, 0, 2],
[0, 0, 2, 1],
[1, 1, 1, 2],
[1, 0, 1, 2]])
gt = np.array([[0, 0, 0, 2],
[0, 0, 2, 1],
[1, 1, 1, 0],
[1, 0, 1, 2]])res = generate_matrix(3,gt,pre)函数中:
mask = (gt_image >= 0) & (gt_image < num_class)
mask:[[ True True True True], [ True True True True], [ True True True True], [ True True True True]]
label = num_class * gt_image[mask].astype('int') + pre_image[mask]其中:gt_image[mask].astype('int')为 [0 0 0 2 0 0 2 1 1 1 1 0 1 0 1 2]
pre_image[mask]为[0 0 0 2 0 0 2 1 1 1 1 2 1 0 1 2]
从第一个数开始 ,gt_image值为0,pre_image值也为0,也就是 label[0] = 0 * 0 + 0 = 0 ,表示的是
在混淆矩阵中,
行代表真实类别,列代表预测的类别,矩阵中(x, y)位置的元素代表该张图片中真实类别为x,被预测为y的个数
通过0 * 0 先确定了为第一行,也就是真实值为0的哪类,然后+0 确定了列,也就是第一列,预测值也为0。依次计算。
得到 label = [0 0 0 8 0 0 8 4 4 4 4 2 4 0 4 8]
因为在混淆矩阵中统计的是次数,就通过
count = np.bincount(label, minlength=num_class ** 2)来计算出0 - num_class ** 2 -1的个数,因为不能保证矩阵中最后一行,最后一列的元素出现过,所以需要指定minlength = num_class ** 2
关于bincount如何使用的可以看https://blog.csdn.net/xlinsist/article/details/51346523
最后得到count=[6 0 1 0 6 0 0 0 3]
confusion_matrix = count.reshape(num_class, num_class)最后通过reshape把一维数据变为混淆矩阵就可以了
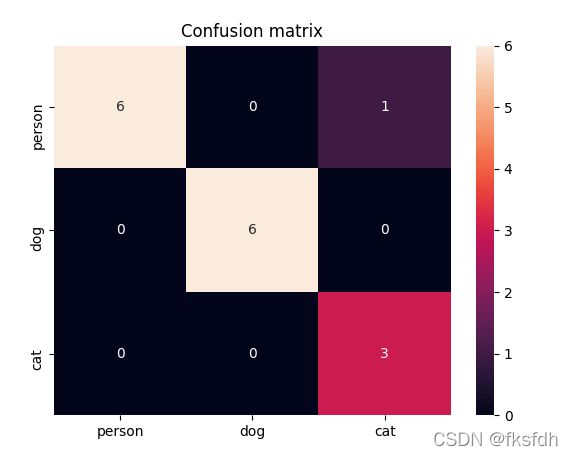
confusion_matrix = [[6 0 1],
[0 6 0],
[0 0 3]]
二、miou
在计算miou之前,先看个函数
np.diag
import numpy as np
test1 = np.arange(1,4)
test2 = np.arange(1,10).reshape(3,3)
res1 = np.diag(test1)
res2 = np.diag(test2)
print("res1:",res1)
print("res2:",res2)结果:
res1: [[1 0 0]
[0 2 0]
[0 0 3]]
res2: [1 5 9]Process finished with exit code 0
1维数组时,会形成一个以一维数组为对角线元素的矩阵
二维矩阵时,输出为矩阵的对角线元素
![]()
IOU=TP/(FP+FN+TP)
代码:
def miou(hist):
iou = np.diag(hist) / (hist.sum(axis=1) + hist.sum(axis=0) - np.diag(hist))
miou = np.nanmean(iou)
return miou其中:
iou = np.diag(hist) / (hist.sum(axis=1) + hist.sum(axis=0) - np.diag(hist))
接着刚才混淆矩阵的例子:
得到的混淆矩阵为:
confusion_matrix = [[6 0 1],
[0 6 0],
[0 0 3]]
np.diag(hist)为[6 6 3]
hist.sum(axis=1)为[7 6 3]
hist.sum(axis=0)为[6 6 4]
hist.sum(axis=1) + hist.sum(axis=0) - np.diag(hist)为[7 6 4],减去np.diag(hist)是因为np.diag(hist)计算了两次,需要减去一次,才会得到并集。
最后 np.diag(hist) / (hist.sum(axis=1) + hist.sum(axis=0) - np.diag(hist)) =
[0.85714286, 1. , 0.75 ]
为每个分类的iou,
通过miou = np.nanmean(iou) 得到最后的miou为0.8690476190476191
最后完整代码:
import numpy as np
# 计算混淆矩阵
def generate_matrix(num_class,gt_image, pre_image):
#正确的gt_mask
mask = (gt_image >= 0) & (gt_image < num_class) # ground truth中所有正确(值在[0, classe_num])的像素label的mask
label = num_class * gt_image[mask].astype('int') + pre_image[mask]
# np.bincount计算了从0到n**2-1这n**2个数中每个数出现的次数,返回值形状(n, n)
count = np.bincount(label, minlength=num_class ** 2)
confusion_matrix = count.reshape(num_class, num_class) # (n, n)
return confusion_matrix
def miou(hist):
iou = np.diag(hist) / (hist.sum(axis=1) + hist.sum(axis=0) - np.diag(hist))
miou = np.nanmean(iou)
return miou
if __name__ == '__main__':
pre = np.array([[0, 0, 0, 2],
[0, 0, 2, 1],
[1, 1, 1, 2],
[1, 0, 1, 2]])
gt = np.array([[0, 0, 0, 2],
[0, 0, 2, 1],
[1, 1, 1, 0],
[1, 0, 1, 2]])
#求混淆矩阵
hist = generate_matrix(3,gt,pre)
#画混淆矩阵热力图
ax = plt.axes()
class_names = ['person', 'dog', 'cat']
sn.heatmap(hist, annot=True,
annot_kws={"size": 10},
xticklabels=class_names,
yticklabels=class_names, ax=ax)
ax.set_title('Confusion matrix')
plt.savefig('./confusion.jpg')
plt.show()
#计算miou
miou_res = miou(hist)
print(miou_res)结果:
混淆矩阵热力图:
miou:0.8690476190476191
参考链接:
1、https://blog.csdn.net/u012370185/article/details/94409933
2、 https://blog.csdn.net/fanzonghao/article/details/84622782