美赛整理之遗传算法优化BP神经网络的齿轮故障诊断问题
遗传算法优化BP神经网络的齿轮故障诊断问题
-
- 一.问题的提出
- 二.问题的分析
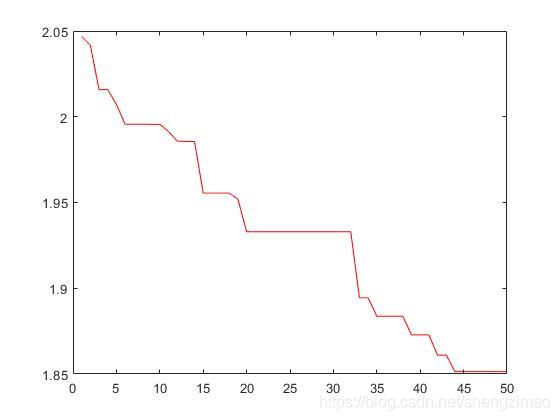
- 三.结果显示
一.问题的提出
二.问题的分析
这里给出了9组15维的向量,我们的目的就是要根据这9组数据来建立一个BP神经网络来识别这任意一个15维的样本特征值向量对应的齿轮状态究竟是无故障,齿根裂纹还是断齿这 3种情况中的哪一种?
在这里我们将齿轮的三种状态分别定义为如下:
无 故 障 : ( 1 , 0 , 0 ) 齿 根 裂 纹 : ( 0 , 1 , 0 ) 断 齿 : ( 0 , 0 , 1 ) 无故障:(1,0,0) \\ 齿根裂纹: (0,1,0) \\ 断齿:(0,0,1) 无故障:(1,0,0)齿根裂纹:(0,1,0)断齿:(0,0,1)
因此,我们应该要建立一个包含一个隐含层的15_31_3的神经网络结构:
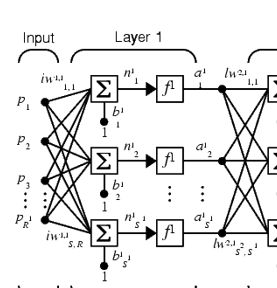
关于如何构建一个上述的神经网络请参考下方百度云链接中的PPT:
提取码:t8mr
该模型建立好了之后我们就要用9组数据中的前5组数据来进行一个初步的训练,用后4组数据来进行测试,并求出最后的误差函数来。
具体的代码如下:
function err = Bpfun(x,P,T,hiddennum,P_test,T_test)
net = newff(minmax(P),[31,3],{'tansig','logsig'},'trainlm');%设置基本的网络参数
net.trainParam.epochs = 1000; %设置训练步数
net.trainParam.goal = 0.01; %设置训练的目标误差
LP.lr = 0.1;
inputnum = size(P,1);
outputnum = size(T,1);
w1num = inputnum*hiddennum;
w2num = outputnum*hiddennum;
w1 = x(1:w1num);
B1 = x(w1num+1:w1num+hiddennum);
w2 = x(w1num+hiddennum+1:w1num+hiddennum+w2num);
B2 = x(w1num+hiddennum+w2num+1:w1num+hiddennum+w2num+outputnum);
net.IW{1,1} = reshape(w1,hiddennum,inputnum);
net.LW{2,1} = reshape(w2,outputnum,hiddennum);
net.b{1} = reshape(B1,hiddennum,1);
net.b{2} = reshape(B2,outputnum,1);
net = train(net,P,T);
Y = sim(net,P_test);
err = norm(Y-T_test);
end
该函数中的x代表一个1行592列的一个行向量。由于是一个15_31_3网络。所以:
其中x前465个值分别代表从输入层到隐含层的15*31个参数的权值。
x中从第466个值到497个值代表隐含层31个神经元各个对应的阈值。
x中从498个值到第589个值代表隐含层到输出层31*3个参数的权值。
x中从第590到第592个值代表输出的3个量对应的阈值。
P代表用来训练的15维向量输入,T代表用来训练的3维向量输出。
P_test代表用来测试的15维向量输入,T_test代表用来测试的3维向量输出。
err代表测试的误差。
用上面的函数就可以求出任意一个初始参数由我们确定的神经网络在实际数据训练之后得到的误差值。
我们接下来的目标就是要用遗传算法来对上述的误差值进行优化,以确定一个能使得误差值达到最小的初始参数x。由于这是一个比较复杂的神经网络,因此不太好用GA工具箱求解,在这里我们采用谢菲尔德工具箱对上面的参数x进行优化。
相关的谢菲尔德工具箱及其安装教程和具体的函数说明:提取码:3uqy
在此,我们将种群设置为含有40个染色体,每个染色体由592*10个0_1变量所组成的种群。其中每10个0_1变量代表一个我们要求的参数。种群的适应度函数定义为误差值神经网络测试后的误差值。整个种群的误差值见下:
function f = Objfun(X,P,T,hiddennum,P_test,T_test)
[m,n] = size(X);
f = zeros(m,1);
for i = 1:m
f(i) = Bpfun(X(i,:),P,T,hiddennum,P_test,T_test);
end
end
f是40*1的列向量,每个值代表任意一个染色体的测试误差值。
具体的遗传算法实现过程如下:
clc,clear;
P_data =load('D:\matlab\bin\matlab搜索路径D盘\BP_神经网络_遗传算法\P_data.txt');
T_data =load('D:\matlab\bin\matlab搜索路径D盘\BP_神经网络_遗传算法\T_data.txt');
P = P_data(:,1:5); %取P_data中的前5组为训练输入数据
T = T_data(:,1:5); %取T_data中的前5组为训练输出数据
P_test = P_data(:,6:9); %取P_data中的前5组为测试输入数据
T_test = T_data(:,6:9); %取T_data中的前5组为测试输出数据
hiddennum = 31;
inputnum = size(P,1);
outputnum = size(T,1);
w1num = inputnum*hiddennum;
w2num = outputnum*hiddennum;
N = w1num+hiddennum+w2num+outputnum;
NIND = 40; %每个种群由40个染色体构成
MAXGEN = 50; %种群进化50代
PRECI = 10; %种群每10个0_1值代表1个未知参数值
GGAP = 0.95;
pm = 0.01; %种群变异概率
px = 0.75; %种群重组概率
Field = zeros(7,N);
for j = 1:N
Field(:,j) = [PRECI;-0.5;0.5;1;0;1;1]; %种群参数选择器
end
chrom = crtbp(NIND,N*PRECI);
gen = 0;trace = zeros(N+1,MAXGEN);
X = bs2rv(chrom,Field); %将每个592*10维的0_1染色体转化成592维的10进制染色体
objv = Objfun(X,P,T,hiddennum,P_test,T_test); %求出适应度值(误差值)
while gen其中P_data和T_data是我们的数据。我放在了我的matlab搜索路径下面了。小伙伴们也可以自行更改路径。