Affinity Propagation: AP聚类算法
算法概述
原文:
[Frey B J, Dueck D. Clustering by passing messages between data points[J]. science, 2007, 315(5814): 972-976.](Frey B J, Dueck D. Clustering by passing messages between data points[J]. science, 2007, 315(5814)
AP聚类一般翻译为近邻传播聚类,07年被提出,其优点有:
1. 不需要制定最终聚类族的个数
2. 已有的数据点作为最终的聚类中心,而不是新生成一个族中心。
3. 模型对数据的初始值不敏感。
4. 对初始相似度矩阵数据的对称性没有要求。
5. 相比与k-centers聚类方法,其结果的平方差误差较小。
基本概念:
* Exemplar范例:即聚类族中心点;
* s(i,j):数据点i与数据点j的相似度值,一般使用欧氏距离的的负值表示,即s(i,j)值越大表示点i与j的距离越近,AP算法中理解为数据点j作为数据点i的聚类中心的能力;
* 相似度矩阵:作为算法的初始化矩阵,n个点就有由n乘n个相似度值组成的矩阵;
* Preference参考度或称为偏好参数:是相似度矩阵中横轴纵轴索引相同的点,如s(i,i),若按欧氏距离计算其值应为0,但在AP聚类中其表示数据点i作为聚类中心的程度,因此不能为0。迭代开始前假设所有点成为聚类中心的能力相同,因此参考度一般设为相似度矩阵中所有值得最小值或者中位数,但是参考度越大则说明个数据点成为聚类中心的能力越强,则最终聚类中心的个数则越多;
* Responsibility,r(i,k):吸引度信息,表示数据点k适合作为数据点i的聚类中心的程度;公式如下:
![]()
其中a(i,k’)表示除k外其他点对i点的归属度值,初始为0;s(i,k’)表示除k外其他点对i的吸引度,即i外其他点都在争夺i点的 所有权;r(i,k)表示数据点k成为数据点i的聚类中心的累积证明,r(i,k)值大于0,则表示数据点k成为聚类中心的能力强。说明:此时只考虑哪个点k成为点i的聚类中心的可能性最大,但是没考虑这个吸引度最大的k是否也经常成为其他点的聚类中心(即归属度),若点k只是点i的聚类中心,不是其他任何点的聚类中心,则会造成最终聚类中心个数大于实际的中心个数。
* Availability,a(i,k):归属度信息,表示数据点i选择数据点k作为其聚类中心的合适程度,公式如下:
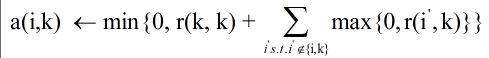
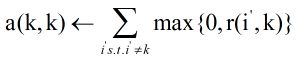
其中r(i’,k)表示点k作为除i外其他点的聚类中心的相似度值,取所有大于等于0的吸引度值,加上k作为聚类中心的可能程。即点k在这些吸引度值大于0的数据点的支持下,数据点i选择k作为其聚类中心的累积证明。
* Damping factor阻尼系数:为防止数据震荡,引入地衰减系数,每个信息值等于前一次迭代更新的信息值的λ倍加上此轮更新值得1-λ倍,其中λ在0-1之间,默认为0.5。
算法流程:
1. 更新相似度矩阵中每个点的吸引度信息,计算归属度信息;
2. 更新归属度信息,计算吸引度信息;
3. 对样本点的吸引度信息和归属度信息求和,检测其选择聚类中心的决策;若经过若干次迭代之后其聚类中心不变、或者迭代次数超过既定的次数、又或者一个子区域内的关于样本点的决策经过数次迭代后保持不变,则算法结束。
关于其算法流程,知乎上kael 用户将AP聚类过程比喻为选举过程:
* 所有人都参加选举(大家都是选民也都是参选人),要选出几个作为代表
* s(i,k)就相当于i对选k这个人的一个固有的偏好程度
* r(i,k)表示用s(i,k)减去最强竞争者的评分,可以理解为k在对i这个选民的竞争中的优势程度
* r(i,k)的更新过程对应选民i对各个参选人的挑选(越出众越有吸引力)
* a(i,k):从公式里可以看到,所有r(i’,k)>0的值都对a有正的加成。对应到我们这个比喻中,就相当于选民i通过网上关于k的民意调查看到:有很多人(即i’们)都觉得k不错(r(i’,k)>0),那么选民i也就会相应地觉得k不错,是个可以相信的选择
* a(i,k)的更新过程对应关于参选人k的民意调查对于选民i的影响(已经有了很多跟随者的人更有吸引力)
* 两者交替的过程也就可以理解为选民在各个参选人之间不断地比较和不断地参考各个参选人给出的民意调查。
* r(i,k)的思想反映的是竞争,a(i,k)则是为了让聚类更成功。
作者:kael
链接:https://www.zhihu.com/question/25384514/answer/47636054
算法缺点:
1. 虽然AP算法不用提前设置聚类中心的个数,但是需要事先设置参考度,而参考度的大小与聚类中心的个数正相关;
2. 由于AP算法每次迭代都需要更新每个数据点的吸引度值和归属度值,算法复杂度较高,在大数据量下运行时间较长。
算法应用:
工具:
Python语言的机器学习库scikit-learn;
* win7-64位下安装scikit-learn:
1. 需要环境
Python (>= 2.6 or >= 3.3),
NumPy (>= 1.6.1),
SciPy (>= 0.9).
可以使用pip安装NumPy和NumPy,也可以直接安装Python(x,y) 即满足scikit-learn的安装环境;
2. cmd调出命令输入界面后,输入pip install -U scikit-learn,即可完成安装;
3. 除此之外,Python科学计算集成开发环境Anaconda中已经自带最新版的scikit-learn包。
* 示例:
from sklearn.cluster import AffinityPropagation
from sklearn import metrics
from sklearn.datasets.samples_generator import make_blobs
# 生成测试数据
centers = [[1, 1], [-1, -1], [1, -1]]
# 生成实际中心为centers的测试样本300个,X是包含300个(x,y)点的二维数组,labels_true为其对应的真是类别标签
X, labels_true = make_blobs(n_samples=300, centers=centers, cluster_std=0.5,
random_state=0)
# 计算AP
ap = AffinityPropagation(preference=-50).fit(X)
cluster_centers_indices = ap.cluster_centers_indices_ # 预测出的中心点的索引,如[123,23,34]
labels = ap.labels_ # 预测出的每个数据的类别标签,labels是一个NumPy数组
n_clusters_ = len(cluster_centers_indices) # 预测聚类中心的个数
print('预测的聚类中心个数:%d' % n_clusters_)
print('同质性:%0.3f' % metrics.homogeneity_score(labels_true, labels))
print('完整性:%0.3f' % metrics.completeness_score(labels_true, labels))
print('V-值: % 0.3f' % metrics.v_measure_score(labels_true, labels))
print('调整后的兰德指数:%0.3f' % metrics.adjusted_rand_score(labels_true, labels))
print('调整后的互信息: %0.3f' % metrics.adjusted_mutual_info_score(labels_true, labels))
print('轮廓系数:%0.3f' % metrics.silhouette_score(X, labels, metric='sqeuclidean'))
# 绘制图表展示
import matplotlib.pyplot as plt
from itertools import cycle
plt.close('all') # 关闭所有的图形
plt.figure(1) # 产生一个新的图形
plt.clf() # 清空当前的图形
colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
# 循环为每个类标记不同的颜色
for k, col in zip(range(n_clusters_), colors):
# labels == k 使用k与labels数组中的每个值进行比较
# 如labels = [1,0],k=0,则‘labels==k’的结果为[False, True]
class_members = labels == k
cluster_center = X[cluster_centers_indices[k]] # 聚类中心的坐标
plt.plot(X[class_members, 0], X[class_members, 1], col + '.')
plt.plot(cluster_center[0], cluster_center[1], markerfacecolor=col,
markeredgecolor='k', markersize=14)
for x in X[class_members]:
plt.plot([cluster_center[0], x[0]], [cluster_center[1], x[1]], col)
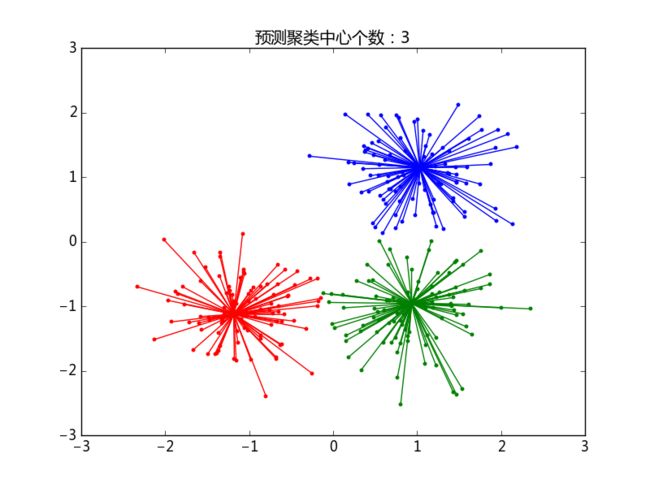
plt.title('预测聚类中心个数:%d' % n_clusters_)
plt.show()```
测试结果: 预测的聚类中心个数:3
同质性:0.872
完整性:0.872
V-值: 0.872
调整后的兰德指数:0.912
调整后的互信息: 0.871
轮廓系数:0.753
“`
参考文献:
聚类(6)– Affinity Propagation Clustering
聚类算法Affinity Propagation(AP)
scikit-learn官网