数据特征分析

分布分析对比分析统计分析帕累托分析正态性检验相关性分析

分布分析

• 分布分析 → 研究数据的分布特征和分布类型，分定量数据、定性数据区分基本统计量

• 极差 / 频率分布情况 / 分组组距及组数

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']

import warnings
warnings.filterwarnings('ignore')

# 数据读取

data = pd.read_csv('./second_hand_ house.csv')
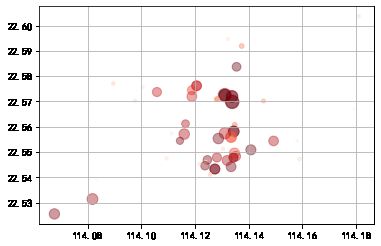
plt.scatter(data['经度'],data['纬度'],  # 按照经纬度显示
            s = data['房屋单价']/500,  # 按照单价显示大小
            c = data['参考总价'],  # 按照总价显示颜色
            alpha = 0.4, cmap = 'Reds')  
plt.grid()
print(data.dtypes)
print('-------\n数据长度为%i条' % len(data))
data.head()
# 通过数据可见，一共8个字段
# 定量字段：房屋单价，参考首付，参考总价，*经度，*纬度，*房屋编码
# 定性字段：小区，朝向

---

房屋编码      int64
小区       object
朝向       object
房屋单价      int64
参考首付    float64
参考总价    float64
经度      float64
纬度      float64
dtype: object
-------
数据长度为75条

# 极差：max-min
# 只针对定量字段

def d_range(df,*cols):
    krange = []
    for col in cols:
        crange = df[col].max() - df[col].min()
        krange.append(crange)
    return(krange)
# 创建函数求极差

key1 = '参考首付'
key2 = '参考总价'
dr = d_range(data,key1,key2)
print('%s极差为 %f \n%s极差为 %f' % (key1, dr[0], key2, dr[1]))
# 求出数据对应列的极差

---

参考首付极差为 52.500000 
参考总价极差为 175.000000

---

# 频率分布情况 - 定量字段
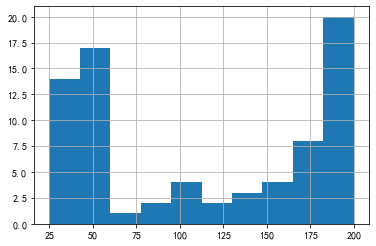
# ① 通过直方图直接判断分组组数

data[key2].hist(bins=10)
# 简单查看数据分布，确定分布组数 → 一般8-16即可
# 这里以10组为参考

# 频率分布情况 - 定量字段
# ② 求出分组区间

gcut = pd.cut(data[key2],10,right=False)
gcut_count = gcut.value_counts(sort=False)  # 不排序
data['%s分组区间' % key2] = gcut.values
print(gcut.head(),'\n------')
print(gcut_count)
data.head()
# pd.cut(x, bins, right)：按照组数对x分组，且返回一个和x同样长度的分组dataframe，right → 是否右边包含，默认True
# 通过groupby查看不同组的数据频率分布
# 给源数据data添加“分组区间”列

---

0      [42.5, 60.0)
1      [25.0, 42.5)
2      [42.5, 60.0)
3      [25.0, 42.5)
4    [165.0, 182.5)
Name: 参考总价, dtype: category
Categories (10, interval[float64]): [[25.0, 42.5) < [42.5, 60.0) < [60.0, 77.5) < [77.5, 95.0) ... [130.0, 147.5) < [147.5, 165.0) < [165.0, 182.5) < [182.5, 200.175)] 
------
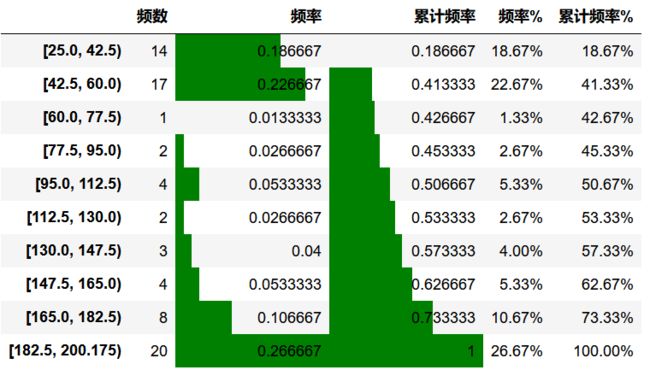
[25.0, 42.5)        14
[42.5, 60.0)        17
[60.0, 77.5)         1
[77.5, 95.0)         2
[95.0, 112.5)        4
[112.5, 130.0)       2
[130.0, 147.5)       3
[147.5, 165.0)       4
[165.0, 182.5)       8
[182.5, 200.175)    20
Name: 参考总价, dtype: int64

# 频率分布情况 - 定量字段
# ③  求出目标字段下频率分布的其他统计量 → 频数，频率，累计频率

r_zj = pd.DataFrame(gcut_count)
r_zj.rename(columns ={gcut_count.name:'频数'}, inplace = True)  # 修改频数字段名
r_zj['频率'] = r_zj / r_zj['频数'].sum()  # 计算频率
r_zj['累计频率'] = r_zj['频率'].cumsum()  # 计算累计频率
r_zj['频率%'] = r_zj['频率'].apply(lambda x: "%.2f%%" % (x*100))  # 以百分比显示频率
r_zj['累计频率%'] = r_zj['累计频率'].apply(lambda x: "%.2f%%" % (x*100))  # 以百分比显示累计频率
r_zj.style.bar(subset=['频率','累计频率'], color='green',width=100)
# 可视化显示

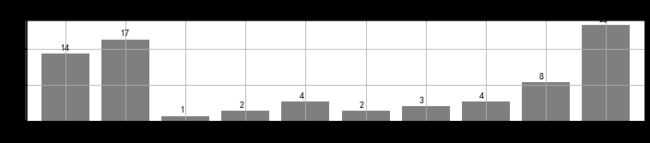
# 频率分布情况 - 定量字段
# ④ 绘制频率直方图

r_zj['频率'].plot(kind = 'bar',
                 width = 0.8,
                 figsize = (12,2),
                 rot = 0,
                 color = 'k',
                 grid = True,
                 alpha = 0.5)
plt.title('参考总价分布频率直方图')
# 绘制直方图

x = len(r_zj)
y = r_zj['频率']
m = r_zj['频数']
for i,j,k in zip(range(x),y,m):
    plt.text(i-0.1,j+0.01,'%i' % k, color = 'k')
# 添加频数标签

# 频率分布情况 - 定性字段
# ① 通过计数统计判断不同类别的频率

cx_g = data['朝向'].value_counts(sort=True)
print(cx_g)
# 统计频率

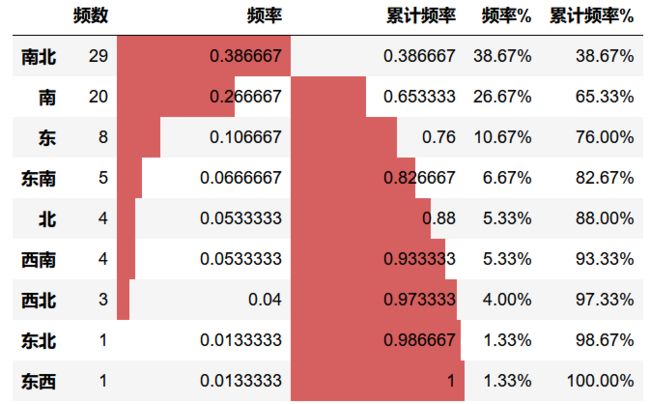
r_cx = pd.DataFrame(cx_g)
r_cx.rename(columns ={cx_g.name:'频数'}, inplace = True)  # 修改频数字段名
r_cx['频率'] = r_cx / r_cx['频数'].sum()  # 计算频率
r_cx['累计频率'] = r_cx['频率'].cumsum()  # 计算累计频率
r_cx['频率%'] = r_cx['频率'].apply(lambda x: "%.2f%%" % (x*100))  # 以百分比显示频率
r_cx['累计频率%'] = r_cx['累计频率'].apply(lambda x: "%.2f%%" % (x*100))  # 以百分比显示累计频率
r_cx.style.bar(subset=['频率','累计频率'], color='#d65f5f',width=100)
# 可视化显示

---

南北    29
南     20
东      8
东南     5
北      4
西南     4
西北     3
东北     1
东西     1
Name: 朝向, dtype: int64

# 频率分布情况 - 定量字段
# ② 绘制频率直方图、饼图

plt.figure(num = 1,figsize = (12,2))
r_cx['频率'].plot(kind = 'bar',
                 width = 0.8,
                 rot = 0,
                 color = 'k',
                 grid = True,
                 alpha = 0.5)
plt.title('参考总价分布频率直方图')
# 绘制直方图

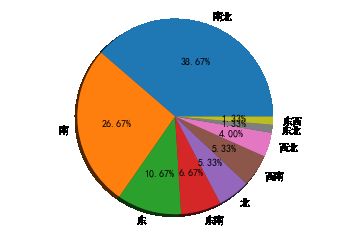
plt.figure(num = 2)
plt.pie(r_cx['频数'],
       labels = r_cx.index,
       autopct='%.2f%%',
       shadow = True)
plt.axis('equal')
# 绘制饼图

---

(-1.1101621526291232,
 1.1004839130571389,
 -1.1062755172910221,
 1.1205348076125872)

对比分析

对比分析 → 两个互相联系的指标进行比较

• 绝对数比较（相减） / 相对数比较（相除）

• 结构分析、比例分析、空间比较分析、动态对比分析

# 1、绝对数比较 → 相减
# 相互对比的指标在量级上不能差别过大
# （1）折线图比较
# （2）多系列柱状图比较

data = pd.DataFrame(np.random.rand(30,2)*1000,
                   columns = ['A_sale','B_sale'],
                   index = pd.period_range('20170601','20170630'))
print(data.head())
# 创建数据 → 30天内A/B产品的日销售额

data.plot(kind='line',
       style = '--.',
       alpha = 0.8,
       figsize = (10,3),
       title = 'AB产品销量对比-折线图')
# 折线图比较

data.plot(kind = 'bar',
          width = 0.8,
          alpha = 0.8,
          figsize = (10,3),
          title = 'AB产品销量对比-柱状图')
# 多系列柱状图比较

---

                A_sale      B_sale
2017-06-01  898.459477  983.505037
2017-06-02  889.767336  564.987465
2017-06-03   35.800165  822.630048
2017-06-04  464.397896  969.447691
2017-06-05  790.681816   80.532220

# 1、绝对数比较 → 相减
# （3）柱状图堆叠图+差值折线图比较

fig3 = plt.figure(figsize=(10,6))
plt.subplots_adjust(hspace=0.3)
# 创建子图及间隔设置

ax1 = fig3.add_subplot(2,1,1)  
x = range(len(data))
y1 = data['A_sale']
y2 = -data['B_sale']
plt.bar(x,y1,width = 1,facecolor = 'yellowgreen')
plt.bar(x,y2,width = 1,facecolor = 'lightskyblue')
plt.title('AB产品销量对比-堆叠图')
plt.grid()
plt.xticks(range(0,30,6))
ax1.set_xticklabels(data.index[::6])
# 创建堆叠图

ax2 = fig3.add_subplot(2,1,2)  
y3 = data['A_sale']-data['B_sale']
plt.plot(x,y3,'--go')

plt.grid()
plt.title('AB产品销量对比-差值折线')
plt.xticks(range(0,30,6))
ax2.set_xticklabels(data.index[::6])
# 创建差值折线图

---

[Text(0, 0, '2017-06-01'),
 Text(0, 0, '2017-06-07'),
 Text(0, 0, '2017-06-13'),
 Text(0, 0, '2017-06-19'),
 Text(0, 0, '2017-06-25')]

# 2、相对数比较 → 相除
# 有联系的指标综合计算后的对比，数值为相对数
# 结构分析、比例分析、空间比较分析、动态对比分析、计划完成度分析
# （1）结构分析
# 在分组基础上，各组总量指标与总体的总量指标对比，计算出各组数量在总量中所占比重
# 反映总体的内部结构

data = pd.DataFrame({'A_sale':np.random.rand(30)*1000,
                    'B_sale':np.random.rand(30)*200},
                   index = pd.period_range('20170601','20170630'))
print(data.head())
print('------')
# 创建数据 → 30天内A/B产品的日销售额
# A/B产品销售额量级不同

data['A_per'] = data['A_sale'] / data['A_sale'].sum()
data['B_per'] = data['B_sale'] / data['B_sale'].sum()
# 计算出每天的营收占比

data['A_per%'] = data['A_per'].apply(lambda x: '%.2f%%' % (x*100))
data['B_per%'] = data['B_per'].apply(lambda x: '%.2f%%' % (x*100))
# 转换为百分数
print(data.head())

fig,axes = plt.subplots(2,1,figsize = (10,6),sharex=True)
data[['A_sale','B_sale']].plot(kind='line',style = '--.',alpha = 0.8,ax=axes[0])
axes[0].legend(loc = 'upper right')
data[['A_per','B_per']].plot(kind='line',style = '--.',alpha = 0.8,ax=axes[1])
axes[1].legend(loc = 'upper right')
# 绝对值对比较难看出结构性变化，通过看销售额占比来看售卖情况的对比

# 同时可以反应“强度” → 两个性质不同但有一定联系的总量指标对比，用来说明“强度”、“密度”、“普遍程度”
# 例如：国内生产总值“元/人”，人口密度“人/平方公里”

---

                A_sale      B_sale
2017-06-01  788.351550    7.045333
2017-06-02  120.555829   61.661209
2017-06-03  595.096291  179.395467
2017-06-04  538.836681  180.161175
2017-06-05  292.155141  197.255793
------
                A_sale      B_sale     A_per     B_per A_per% B_per%
2017-06-01  788.351550    7.045333  0.063815  0.002420  6.38%  0.24%
2017-06-02  120.555829   61.661209  0.009759  0.021176  0.98%  2.12%
2017-06-03  595.096291  179.395467  0.048171  0.061609  4.82%  6.16%
2017-06-04  538.836681  180.161175  0.043617  0.061871  4.36%  6.19%
2017-06-05  292.155141  197.255793  0.023649  0.067742  2.36%  6.77%

# 2、相对数比较 → 相除
# （2）比例分析
# 在分组的基础上，将总体不同部分的指标数值进行对比，其相对指标一般称为“比例相对数”
# 比例相对数 = 总体中某一部分数值 / 总体中另一部分数值 → “基本建设投资额中工业、农业、教育投资的比例”、“男女比例”...

data = pd.DataFrame({'consumption':np.random.rand(12)*1000 + 2000,
                    'salary':np.random.rand(12)*500 + 5000},
                   index = pd.period_range('2017/1','2017/12',freq = 'M'))
print(data.head())
print('------')
# 创建数据 → 某人一年内的消费、工资薪水情况
# 消费按照2000-3000/月随机，工资按照5000-5500/月随机

data['c_s'] = data['consumption'] / data['salary']
print(data.head())
# 比例相对数 → 消费收入比

data['c_s'].plot.area(color = 'green',alpha = 0.5,ylim = [0.3,0.6],figsize=(8,3),grid=True)
# 创建面积图表达

---

         consumption       salary
2017-01  2367.546836  5027.461740
2017-02  2131.887154  5392.837184
2017-03  2718.487356  5030.931088
2017-04  2537.562204  5020.013155
2017-05  2044.953430  5388.826296
------
         consumption       salary       c_s
2017-01  2367.546836  5027.461740  0.470923
2017-02  2131.887154  5392.837184  0.395318
2017-03  2718.487356  5030.931088  0.540355
2017-04  2537.562204  5020.013155  0.505489
2017-05  2044.953430  5388.826296  0.379480

# 2、相对数比较 → 相除
# （3）空间比较分析（横向对比分析）
# 同类现象在同一时间不同空间的指标数值进行对比，反应同类现象在不同空间上的差异程度和现象发展不平衡的状况
# 空间比较相对数 = 甲空间某一现象的数值 / 乙空间同类现象的数值
# 一个很现实的例子 → 绝对数来看，我国多经济总量世界第一，但从人均水平来看是另一回事

data = pd.DataFrame({'A':np.random.rand(30)*5000,
                    'B':np.random.rand(30)*2000,
                    'C':np.random.rand(30)*10000,
                    'D':np.random.rand(30)*800},
                   index = pd.period_range('20170601','20170630'))
print(data.head())
print('------')
# 创建数据 → 30天内A/B/C/D四个产品的销售情况
# 不同产品的销售量级不同

data.sum().plot(kind = 'bar',color = ['r','g','b','k'], alpha = 0.8, grid = True)
for i,j in zip(range(4),data.sum()):
    plt.text(i-0.25,j+2000,'%.2f' % j, color = 'k')
# 通过柱状图做横向比较 → 4个产品的销售额总量

data[:10].plot(kind = 'bar',color = ['r','g','b','k'], alpha = 0.8, grid = True, figsize = (12,4),width = 0.8)
# 多系列柱状图，横向比较前十天4个产品的销售额

# 关于同比与环比
# 同比 → 产品A在2015.3和2016.3的比较（相邻时间段的同一时间点）
# 环比 → 产品A在2015.3和2015.4的比较（相邻时间段的比较）
# 如何界定“相邻时间段”与“时间点”，决定了是同比还是环比

---

                      A            B            C           D
2017-06-01  1147.137160   895.131991  9139.714963   73.646466
2017-06-02   278.601470  1492.631014  5914.616125  567.150857
2017-06-03  3339.303088   982.091208  2228.577967  453.254696
2017-06-04  2288.918723   679.316592  1487.555250  323.685984
2017-06-05  2062.041882    19.731936  1007.320769  520.285870
------

# 2、相对数比较 → 相除
# （4）动态对比分析（纵向对比分析）
# 同一现象在不同时间上的指标数值进行对比，反应现象的数量随着时间推移而发展变动的程度及趋势
# 最基本方法，计算动态相对数 → 发展速度
# 动态相对数（发展速度） = 某一现象的报告期数值 / 同一现象的基期数值
# 基期：用来比较的基础时期
# 报告期：所要研究的时期，又称计算期

data = pd.DataFrame({'A':np.random.rand(30)*2000+1000},
                   index = pd.period_range('20170601','20170630'))
print(data.head())
print('------')
# 创建数据 → 30天内A产品的销售情况

data['base'] = 1000  # 假设基期销售额为1000，后面每一天都为计算期
data['l_growth'] = data['A'] - data['base']  # 累计增长量 = 报告期水平 - 固定基期水平
data['z_growth'] = data['A'] - data.shift(1)['A']  # 逐期增长量 = 报告期水平 - 报告期前一期水平
data[data.isnull()] = 0  # 替换缺失值

data[['l_growth','z_growth']].plot(figsize = (10,4),style = '--.',alpha = 0.8)  

plt.legend(loc = 'lower left')
plt.grid()
# 通过折线图查看增长量情况

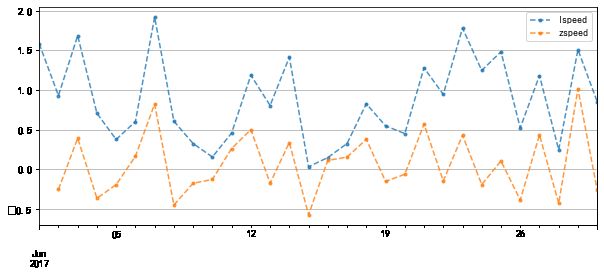
data['lspeed'] = data['l_growth'] / data['base']  # 定基增长速度
data['zspeed'] = data['z_growth'] / data.shift(1)['A']  # 环比增长速度
data[['lspeed','zspeed']].plot(figsize = (10,4),style = '--.',alpha = 0.8)  

plt.grid()
print(data.head())
print('------')
# 通过折线图查看发展速度

---

                      A
2017-06-01  2583.275930
2017-06-02  1929.318167
2017-06-03  2684.675461
2017-06-04  1706.227001
2017-06-05  1376.309872
------
                      A  base     l_growth    z_growth    lspeed    zspeed
2017-06-01  2583.275930  1000  1583.275930    0.000000  1.583276       NaN
2017-06-02  1929.318167  1000   929.318167 -653.957763  0.929318 -0.253151
2017-06-03  2684.675461  1000  1684.675461  755.357294  1.684675  0.391515
2017-06-04  1706.227001  1000   706.227001 -978.448460  0.706227 -0.364457
2017-06-05  1376.309872  1000   376.309872 -329.917130  0.376310 -0.193361
------

统计分析

统计指标对定量数据进行统计描述，常从集中趋势和离中趋势两个方面进行分析

集中趋势度量 / 离中趋势度量

# 1、集中趋势度量
# 指一组数据向某一中心靠拢的倾向，核心在于寻找数据的代表值或中心值 —— 统计平均数
# 算数平均数、位置平均数
# （1）算数平均数

data = pd.DataFrame({'value':np.random.randint(100,120,100),
                    'f':np.random.rand(100)})
data['f'] = data['f'] / data['f'].sum()  # f为权重，这里将f列设置成总和为1的权重占比
print(data.head())
print('------')
# 创建数据

mean = data['value'].mean()
print('简单算数平均值为：%.2f' % mean)
# 简单算数平均值 = 总和 / 样本数量 （不涉及权重）

mean_w = (data['value'] * data['f']).sum() / data['f'].sum()
print('加权算数平均值为：%.2f' % mean_w)
# 加权算数平均值 = (x1f1 + x2f2 + ... + xnfn) / (f1 + f2 + ... + fn)

---

   value         f
0    104  0.014649
1    113  0.000299
2    108  0.008690
3    117  0.005669
4    110  0.005453
------
简单算数平均值为：109.41
加权算数平均值为：109.31

# 1、集中趋势度量
# （2）位置平均数

m = data['value'].mode()
print('众数为',m.tolist())
# 众数是一组数据中出现次数最多的数，这里可能返回多个值

med = data['value'].median()
print('中位数为%i' % med)
# 中位数指将总体各单位标志按照大小顺序排列后，中间位置的数字

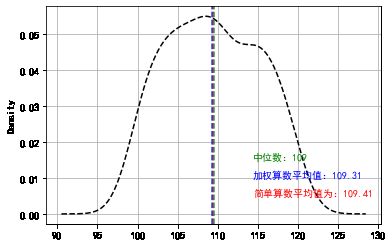
data['value'].plot(kind = 'kde',style = '--k',grid = True)
# 密度曲线

plt.axvline(mean,color='r',linestyle="--",alpha=0.8)  
plt.text(mean + 5,0.005,'简单算数平均值为：%.2f' % mean, color = 'r')
# 简单算数平均值

plt.axvline(mean_w,color='b',linestyle="--",alpha=0.8)  
plt.text(mean + 5,0.01,'加权算数平均值：%.2f' % mean_w, color = 'b')
# 加权算数平均值

plt.axvline(med,color='g',linestyle="--",alpha=0.8)  
plt.text(mean + 5,0.015,'中位数：%i' % med, color = 'g')
# 中位数
# **这里三个数text显示的横坐标一致，目的是图示效果不拥挤

---

众数为 [110]
中位数为109





Text(114.41, 0.015, '中位数：109')

# 2、离中趋势度量
# 指一组数据中各数据以不同程度的距离偏离中心的趋势
# 极差与分位差、方差与标准差、离散系数

data = pd.DataFrame({'A_sale':np.random.rand(30)*1000,
                    'B_sale':np.random.rand(30)*1000},
                   index = pd.period_range('20170601','20170630'))
print(data.head())
print('------')
# 创建数据
# A/B销售额量级在同一水平

---

                A_sale      B_sale
2017-06-01  940.281237  790.613506
2017-06-02  297.537305  754.018901
2017-06-03  134.394969   73.066782
2017-06-04  376.272644  525.635787
2017-06-05  505.534473  176.218216
------

# 2、离中趋势度量
# （1）极差、分位差

data = pd.DataFrame({'A_sale':np.random.rand(30)*1000,
                    'B_sale':np.random.rand(30)*1000},
                   index = pd.period_range('20170601','20170630'))
print(data.head())
print('------')
# 创建数据
# A/B销售额量级在同一水平

a_r = data['A_sale'].max() - data['A_sale'].min()
b_r = data['B_sale'].max() - data['B_sale'].min()
print('A销售额的极差为：%.2f, B销售额的极差为：%.2f' % (a_r,b_r))
print('------')
# 极差
# 没有考虑中间变量的变动，测定离中趋势不稳定

sta = data['A_sale'].describe()
stb = data['B_sale'].describe()
#print(sta)
a_iqr = sta.loc['75%'] - sta.loc['25%']
b_iqr = stb.loc['75%'] - stb.loc['25%']
print('A销售额的分位差为：%.2f, B销售额的分位差为：%.2f' % (a_iqr,b_iqr))
print('------')
# 分位差

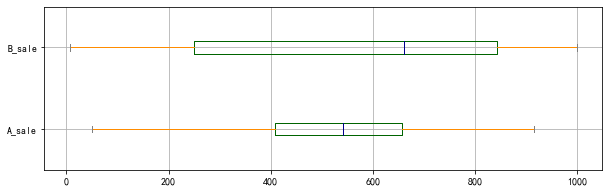
color = dict(boxes='DarkGreen', whiskers='DarkOrange', medians='DarkBlue', caps='Gray')
data.plot.box(vert=False,grid = True,color = color,figsize = (10,3))
# 箱型图

---

                A_sale      B_sale
2017-06-01  149.426607  887.830156
2017-06-02  818.302606  824.220912
2017-06-03  405.221966  998.834052
2017-06-04  541.493479  703.297342
2017-06-05  587.232880  690.739991
------
A销售额的极差为：864.39, B销售额的极差为：992.39
------
A销售额的分位差为：248.45, B销售额的分位差为：592.86
------

# 2、离中趋势度量
# （2）方差与标准差

a_std = sta.loc['std']
b_std = stb.loc['std']
a_var = data['A_sale'].var()
b_var = data['B_sale'].var()
print('A销售额的标准差为：%.2f, B销售额的标准差为：%.2f' % (a_std,b_std))
print('A销售额的方差为：%.2f, B销售额的方差为：%.2f' % (a_var,b_var))
# 方差 → 各组中数值与算数平均数离差平方的算术平均数
# 标准差 → 方差的平方根
# 标准差是最常用的离中趋势指标 → 标准差越大，离中趋势越明显

fig = plt.figure(figsize = (12,4))
ax1 = fig.add_subplot(1,2,1)
data['A_sale'].plot(kind = 'kde',style = 'k--',grid = True,title = 'A密度曲线')
plt.axvline(sta.loc['50%'],color='r',linestyle="--",alpha=0.8)  
plt.axvline(sta.loc['50%'] - a_std,color='b',linestyle="--",alpha=0.8)  
plt.axvline(sta.loc['50%'] + a_std,color='b',linestyle="--",alpha=0.8)  
# A密度曲线，1个标准差

ax2 = fig.add_subplot(1,2,2)
data['B_sale'].plot(kind = 'kde',style = 'k--',grid = True,title = 'B密度曲线')
plt.axvline(stb.loc['50%'],color='r',linestyle="--",alpha=0.8)  
plt.axvline(stb.loc['50%'] - b_std,color='b',linestyle="--",alpha=0.8)  
plt.axvline(stb.loc['50%'] + b_std,color='b',linestyle="--",alpha=0.8)  
# B密度曲线，1个标准差

---

A销售额的标准差为：199.44, B销售额的标准差为：342.41
A销售额的方差为：39777.97, B销售额的方差为：117243.75

帕累托分析

帕累托分析（贡献度分析） → 帕累托法则：20/80定律

“原因和结果、投入和产出、努力和报酬之间本来存在着无法解释的不平衡。一般来说，投入和努力可以分为两种不同的类型：
多数，它们只能造成少许的影响；少数，它们造成主要的、重大的影响。”
→ 一个公司，80%利润来自于20%的畅销产品，而其他80%的产品只产生了20%的利润

例如：

• 世界上大约80％的资源是由世界上15％的人口所耗尽的

• 世界财富的80％为25％的人所拥有；在一个国家的医疗体系中

• 20％的人口与20％的疾病，会消耗80％的医疗资源

一个思路：通过二八原则，去寻找关键的那20%决定性因素！

# 帕累托分布分析 

data = pd.Series(np.random.randn(10)*1200+3000,
                index = list('ABCDEFGHIJ'))
print(data)
print('------')
# 创建数据，10个品类产品的销售额

data.sort_values(ascending=False, inplace= True)
# 由大到小排列

plt.figure(figsize = (10,4))
data.plot(kind = 'bar', color = 'g', alpha = 0.5, width = 0.7)  
plt.ylabel('营收_元')
# 创建营收柱状图

p = data.cumsum()/data.sum()  # 创建累计占比，Series
key = p[p>0.8].index[0]  
key_num = data.index.tolist().index(key) 
print('超过80%累计占比的节点值索引为：' ,key)
print('超过80%累计占比的节点值索引位置为：' ,key_num)
print('------')
# 找到累计占比超过80%时候的index
# 找到key所对应的索引位置

p.plot(style = '--ko', secondary_y=True)  # secondary_y → y副坐标轴
plt.axvline(key_num,color='r',linestyle="--",alpha=0.8)  
plt.text(key_num+0.2,p[key],'累计占比为：%.3f%%' % (p[key]*100), color = 'r')  # 累计占比超过80%的节点
plt.ylabel('营收_比例')
# 绘制营收累计占比曲线

key_product = data.loc[:key]
print('核心产品为：')
print(key_product)
# 输出决定性因素产品

---

A    2521.266064
B    2212.651503
C    4484.516575
D    1561.588461
E    3162.616010
F    1277.677820
G    2249.340201
H    1153.083774
I    5176.326034
J    3056.820423
dtype: float64
------
超过80%累计占比的节点值索引为： B
超过80%累计占比的节点值索引位置为：6
------
核心产品为：
I    5176.326034
C    4484.516575
E    3162.616010
J    3056.820423
A    2521.266064
G    2249.340201
B    2212.651503
dtype: float64

正态性检验

利用观测数据判断总体是否服从正态分布的检验称为正态性检验，它是统计判决中重要的一种特殊的拟合优度假设检验。

直方图初判 / QQ图判断 / K-S检验

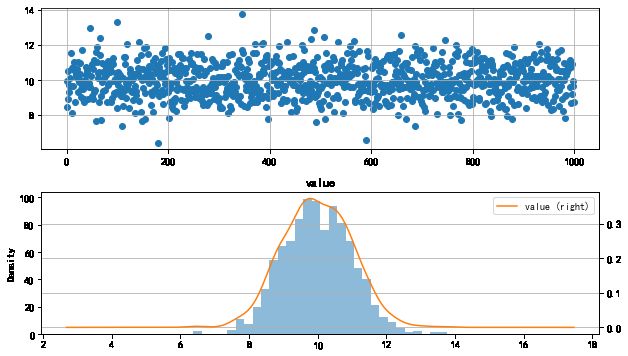
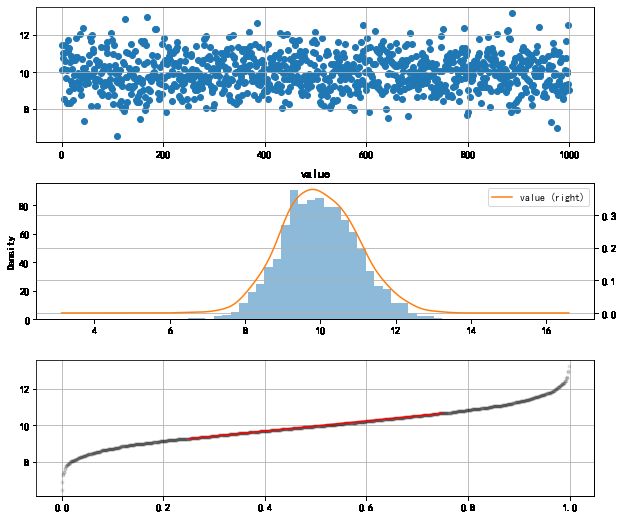
# 直方图初判

s = pd.DataFrame(np.random.randn(1000)+10,columns = ['value'])
print(s.head())
# 创建随机数据

fig = plt.figure(figsize = (10,6))
ax1 = fig.add_subplot(2,1,1)  # 创建子图1
ax1.scatter(s.index, s.values)
plt.grid()
# 绘制数据分布图

ax2 = fig.add_subplot(2,1,2)  # 创建子图2
s.hist(bins=30,alpha = 0.5,ax = ax2)
s.plot(kind = 'kde', secondary_y=True,ax = ax2)
plt.grid()
# 绘制直方图
# 呈现较明显的正太性

---

       value
0   9.960856
1   8.425936
2   8.911952
3  10.498224
4   9.688833

# QQ图判断
# QQ图通过把测试样本数据的分位数与已知分布相比较，从而来检验数据的分布情况

# QQ图是一种散点图，对应于正态分布的QQ图，就是由标准正态分布的分位数为横坐标，样本值为纵坐标的散点图
# 参考直线：四分之一分位点和四分之三分位点这两点确定，看散点是否落在这条线的附近

# 绘制思路
# ① 在做好数据清洗后，对数据进行排序（次序统计量：x(1)

---

       value
0  10.094258
1  11.445694
2  11.038591
3  10.772003
4   8.538419
均值为：9.98，标准差为：1.00
------
   index     value       p         q
0    109  6.495955 -0.0005 -3.495069
1    976  6.923548  0.0005 -3.065968
2    964  7.299486  0.0015 -2.688704
3     45  7.335662  0.0025 -2.652401
4    155  7.434686  0.0035 -2.553027
------
四分之一位数为：9.28，四分之三位数为：10.66
------

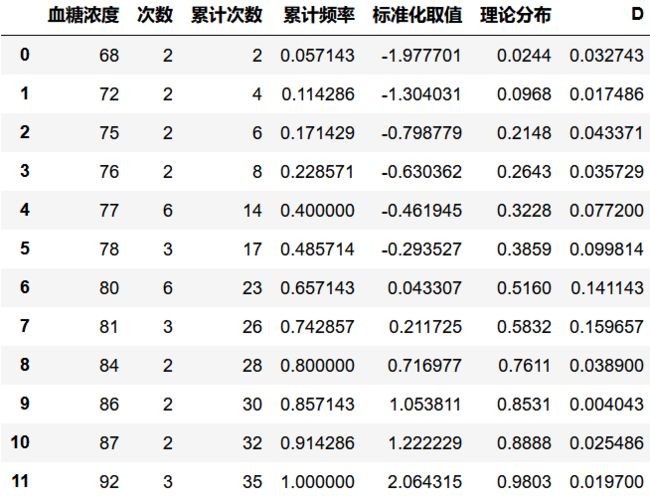
# KS检验，理论推导

data = [87,77,92,68,80,78,84,77,81,80,80,77,92,86,
       76,80,81,75,77,72,81,72,84,86,80,68,77,87,
       76,77,78,92,75,80,78]
# 样本数据，35位健康男性在未进食之前的血糖浓度

df = pd.DataFrame(data, columns =['value'])
u = df['value'].mean()
std = df['value'].std()
print("样本均值为：%.2f，样本标准差为：%.2f" % (u,std))
print('------')
# 查看数据基本统计量

s = df['value'].value_counts().sort_index()
df_s = pd.DataFrame({'血糖浓度':s.index,'次数':s.values})
# 创建频率数据

df_s['累计次数'] = df_s['次数'].cumsum()
df_s['累计频率'] = df_s['累计次数'] / len(data)
df_s['标准化取值'] = (df_s['血糖浓度'] - u) / std
df_s['理论分布'] =[0.0244,0.0968,0.2148,0.2643,0.3228,0.3859,0.5160,0.5832,0.7611,0.8531,0.8888,0.9803]  # 通过查阅正太分布表
df_s['D'] = np.abs(df_s['累计频率'] - df_s['理论分布'])
dmax = df_s['D'].max()
print("实际观测D值为：%.4f" % dmax)
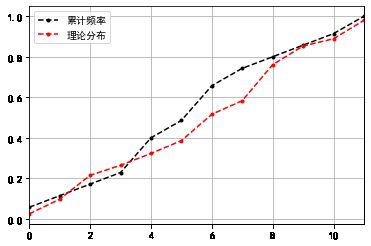
# D值序列计算结果表格

df_s['累计频率'].plot(style = '--k.')
df_s['理论分布'].plot(style = '--r.')
plt.legend(loc = 'upper left')
plt.grid()
# 密度图表示

df_s

---

样本均值为：79.74，样本标准差为：5.94
------
实际观测D值为：0.1597

# 直接用算法做KS检验

from scipy import stats
# scipy包是一个高级的科学计算库，它和Numpy联系很密切，Scipy一般都是操控Numpy数组来进行科学计算

data = [87,77,92,68,80,78,84,77,81,80,80,77,92,86,
       76,80,81,75,77,72,81,72,84,86,80,68,77,87,
       76,77,78,92,75,80,78]
# 样本数据，35位健康男性在未进食之前的血糖浓度

df = pd.DataFrame(data, columns =['value'])
u = df['value'].mean()  # 计算均值
std = df['value'].std()  # 计算标准差
stats.kstest(df['value'], 'norm', (u, std))
# .kstest方法：KS检验，参数分别是：待检验的数据，检验方法（这里设置成norm正态分布），均值与标准差
# 结果返回两个值：statistic → D值，pvalue → P值
# p值大于0.05，为正态分布

---

KstestResult(statistic=0.1590180704824098, pvalue=0.3066297258358026)

相关性分析

分析连续变量之间的线性相关程度的强弱

图示初判 / Pearson相关系数（皮尔逊相关系数） / Sperman秩相关系数（斯皮尔曼相关系数）

# 图示初判
# （1）变量之间的线性相关性

data1 = pd.Series(np.random.rand(50)*100).sort_values()
data2 = pd.Series(np.random.rand(50)*50).sort_values()
data3 = pd.Series(np.random.rand(50)*500).sort_values(ascending = False)
# 创建三个数据：data1为0-100的随机数并从小到大排列，data2为0-50的随机数并从小到大排列，data3为0-500的随机数并从大到小排列，

fig = plt.figure(figsize = (10,4))
ax1 = fig.add_subplot(1,2,1)
ax1.scatter(data1, data2)
plt.grid()
# 正线性相关

ax2 = fig.add_subplot(1,2,2)
ax2.scatter(data1, data3)
plt.grid()
# 负线性相关

---

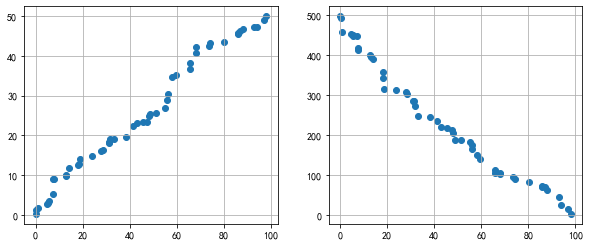
# 图示初判
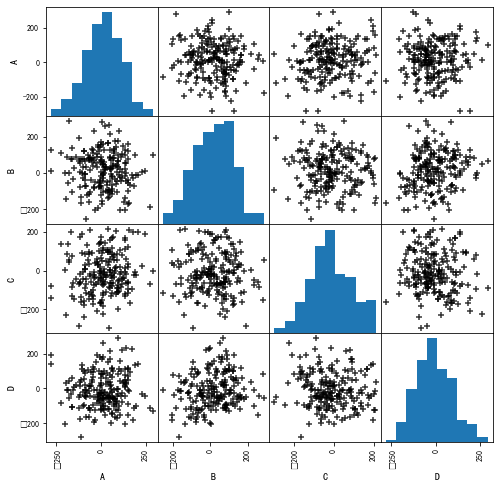
# （2）散点图矩阵初判多变量间关系

data = pd.DataFrame(np.random.randn(200,4)*100, columns = ['A','B','C','D'])
pd.plotting.scatter_matrix(data,figsize=(8,8),
                  c = 'k',
                 marker = '+',
                 diagonal='hist',
                 alpha = 0.8,
                 range_padding=0.1)
data.head()

---

# Pearson相关系数

data1 = pd.Series(np.random.rand(100)*100).sort_values()
data2 = pd.Series(np.random.rand(100)*50).sort_values()
data = pd.DataFrame({'value1':data1.values,
                     'value2':data2.values})
print(data.head())
print('------')
# 创建样本数据

u1,u2 = data['value1'].mean(),data['value2'].mean()  # 计算均值
std1,std2 = data['value1'].std(),data['value2'].std()  # 计算标准差
print('value1正态性检验：\n',stats.kstest(data['value1'], 'norm', (u1, std1)))
print('value2正态性检验：\n',stats.kstest(data['value2'], 'norm', (u2, std2)))
print('------')
# 正态性检验 → pvalue >0.05

data['(x-u1)*(y-u2)'] = (data['value1'] - u1) * (data['value2'] - u2)
data['(x-u1)**2'] = (data['value1'] - u1)**2
data['(y-u2)**2'] = (data['value2'] - u2)**2
print(data.head())
print('------')
# 制作Pearson相关系数求值表

r = data['(x-u1)*(y-u2)'].sum() / (np.sqrt(data['(x-u1)**2'].sum() * data['(y-u2)**2'].sum()))
print('Pearson相关系数为：%.4f' % r)
# 求出r
# |r| > 0.8 → 高度线性相关

---

     value1    value2
0  2.337418  0.157360
1  3.211793  1.166283
2  4.452706  1.581767
3  6.001138  2.189377
4  9.350329  2.392487
------
value1正态性检验：
 KstestResult(statistic=0.09146392896413336, pvalue=0.3533007803300623)
value2正态性检验：
 KstestResult(statistic=0.08594659117892778, pvalue=0.43140134295276117)
------
     value1    value2  (x-u1)*(y-u2)    (x-u1)**2   (y-u2)**2
0  2.337418  0.157360    1265.238118  2606.315250  614.211000
1  3.211793  1.166283    1192.942792  2517.802507  565.220068
2  4.452706  1.581767    1143.108404  2394.809970  545.636956
3  6.001138  2.189377    1078.145157  2245.657088  517.619981
4  9.350329  2.392487     993.002032  1939.448765  508.419224
------
Pearson相关系数为：0.9964

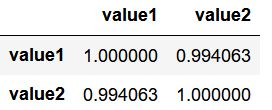
# Pearson相关系数 - 算法

data1 = pd.Series(np.random.rand(100)*100).sort_values()
data2 = pd.Series(np.random.rand(100)*50).sort_values()
data = pd.DataFrame({'value1':data1.values,
                     'value2':data2.values})
print(data.head())
print('------')
# 创建样本数据

data.corr()
# pandas相关性方法：data.corr(method='pearson', min_periods=1) → 直接给出数据字段的相关系数矩阵
# method默认pearson

---

     value1    value2
0  0.131535  0.457501
1  0.633676  1.070184
2  3.075753  1.081241
3  3.545399  1.812641
4  3.830652  2.895861
------

# Sperman秩相关系数

data = pd.DataFrame({'智商':[106,86,100,101,99,103,97,113,112,110],
                    '每周看电视小时数':[7,0,27,50,28,29,20,12,6,17]})
print(data)
print('------')
# 创建样本数据

data.sort_values('智商', inplace=True)
data['range1'] = np.arange(1,len(data)+1)
data.sort_values('每周看电视小时数', inplace=True)
data['range2'] = np.arange(1,len(data)+1)
print(data)
print('------')
# “智商”、“每周看电视小时数”重新按照从小到大排序，并设定秩次index

data['d'] = data['range1'] - data['range2']
data['d2'] = data['d']**2
print(data)
print('------')
# 求出di，di2

n = len(data)
rs = 1 - 6 * (data['d2'].sum()) / (n * (n**2 - 1))
print('Pearson相关系数为：%.4f' % rs)
# 求出rs

---

    智商  每周看电视小时数
0  106         7
1   86         0
2  100        27
3  101        50
4   99        28
5  103        29
6   97        20
7  113        12
8  112         6
9  110        17
------
    智商  每周看电视小时数  range1  range2
1   86         0       1       1
8  112         6       9       2
0  106         7       7       3
7  113        12      10       4
9  110        17       8       5
6   97        20       2       6
2  100        27       4       7
4   99        28       3       8
5  103        29       6       9
3  101        50       5      10
------
    智商  每周看电视小时数  range1  range2  d  d2
1   86         0       1       1  0   0
8  112         6       9       2  7  49
0  106         7       7       3  4  16
7  113        12      10       4  6  36
9  110        17       8       5  3   9
6   97        20       2       6 -4  16
2  100        27       4       7 -3   9
4   99        28       3       8 -5  25
5  103        29       6       9 -3   9
3  101        50       5      10 -5  25
------
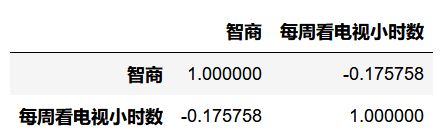
Pearson相关系数为：-0.1758

---

# Pearson相关系数 - 算法

data = pd.DataFrame({'智商':[106,86,100,101,99,103,97,113,112,110],
                    '每周看电视小时数':[7,0,27,50,28,29,20,12,6,17]})
print(data)
print('------')
# 创建样本数据

data.corr(method='spearman')
# pandas相关性方法：data.corr(method='pearson', min_periods=1) → 直接给出数据字段的相关系数矩阵
# method默认pearson

---

    智商  每周看电视小时数
0  106         7
1   86         0
2  100        27
3  101        50
4   99        28
5  103        29
6   97        20
7  113        12
8  112         6
9  110        17
------