MDP模型之Grid World(Q Learining方法)

本次博客依然是伯克利大学的Grid World作业，对应的是Question 6和Question 7。

上次的作业“MDP模型之Grid World(值迭代方法)”，链接为https://blog.csdn.net/weixin_42763696/article/details/105333539

在上一次的作业中，我们已经了解了如何使用值迭代方法求解Grid World，那么Q Learning方法又是什么呢？自然，Q Learning也是一种强化学习的方法，那么它和值迭代又有什么区别呢？这就要从两者的算法思路开始讲了。

1. 值迭代的局限性

首先让我们梳理一下值迭代的步骤

1. 遍历每一个state(格子)
2. 遍历当前state的每一个合法action(上下左右)
3. 对执行action移动到的所有state’的reward进行求和
4. 保存能获得最大reward的action，并将reward值记录在格子(state)上

强化学习作为一种算法，肯定是用来解决现实世界的问题的，但是在值迭代的算法步骤中，是有两步在现实中很难获取到的：

• 第一步：现实世界中，你不可能获得所有的状态，比如一个没有平面图的迷宫，每一条路都是陌生的。
• 第三步：现实世界中，到下一个状态的概率不可能是一个固定值，你永远不知道在吃完午饭后，下午上课老师点到你的概率是多少(午饭state->执行吃饭action->被点名state')。

第三步还有补充的一点，就是现实生活中的action不可能是固定的上下左右，在午饭state我可以执行回宿舍action, 不吃饭action, 玩手机action, 学习action…等等无数种行动，并且无论执行哪个action，都无法知道被点名state'的概率。

这样看来，值迭代有很明显的局限性，为了用强化学习解决更多的问题，所引申出的算法就是Q Learning。

2. Q Learning是怎么做的

Q Learning采用的是一种不断试错方式学习，针对上面两步，Q Learning使用了下面的解决办法

1. 计算的时候不会遍历所有的格子，只管当前状态，当前格子的reward值
2. 不会计算所有action的reward，每次行动时，只选取一个action，只计算这一个action的reward

值迭代在计算reward的时候，会得到每个action的reward，并保留最大的。

而Q Learning在计算reward的时候，虽然也会每个action的reward，但会全部都保留下来。

Q Learning的公式如下：
$$q_{\pi }(s,a)=q_{\pi }(s,a)+\alpha [R+\gamma \underset{a^{\prime }}{\max }{q}_{\pi }(s^{\prime },a^{\prime })-q_{\pi }(s,a)]$$
整理后得到
$$q_{\pi }(s,a)=(1-\alpha )q_{\pi }(s,a)+\alpha [R+\gamma \underset{a^{\prime }}{\max }{q}_{\pi }(s^{\prime },a^{\prime })]$$

从前往后梳理一下公式：

• $q_{\pi }(s,a)$表示的是在s时执行a的reward值之和，包括了经验reward值和新的reward值的相加。

• $(1-\alpha )q_{\pi }(s,a)$表示的是经验reward，即学习率*之前学习到的执行该action的reward。可以看到学习速率α越大，保留之前训练的效果就越少。

• $\alpha [R+\gamma \underset{a^{\prime }}{\max }{q}_{\pi }(s^{\prime },a^{\prime })]$就是新的reward值了，下面逐步拆解。

• $\gamma \underset{a^{\prime }}{\max }{q}_{\pi }(s^{\prime },a^{\prime })$是计算下一个state’中最大的reward值，这个称之为“记忆奖励”。因为在之前某次到达state’的时候，保存了四个方向(a’)的reward值，通过“回忆”，想起来自己之前在state’上能收获的最大好处，就可以直接影响在当前state时reward的计算。$\gamma$是用来增加or减少state’的影响的，$\gamma$越大，智能体就会越重视以往经验，越小，就只重视眼前利益（R）。

• R是执行了action后的reward，比如在终点处执行exit，获得+1/-1的reward。

接下来继续通过模拟的方式理解Q Learning的过程

3. 在Grid World 使用 Q Learning

图1 初始状态 在初始状态下，智能体被扔到了Grid World的起点，此时包括终点在内的每个格子的reward都是未知的，这些都会在智能体的脚踏到那个格子上的时候才会明朗。

接下来让我们向上走一步，走到(0,1)：

图2 向上走了一步

什么事情都没有发生，这是因为智能体在踩到下一个状态后，发现奖励值为0，因此没有任何值的更新。

这种情况会一直保持下去，智能体继续向上走，并且右转弯

图3 走了好多步

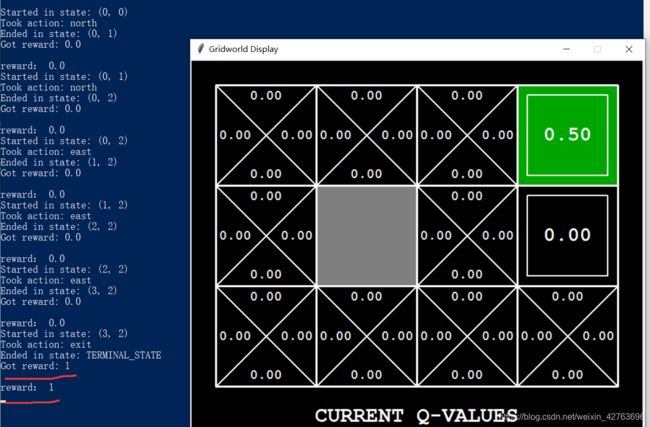
直到我走到了终点(3,2)，执行下一步动作exit的时候，智能体能够获得的reward是1，也就是上述公式中R的值为1。

图4 此时只是待在右上角的(3,2)，还没有执行动作exit

图5 在(3,2)执行exit步骤后，左下角可以看到，reward为1
将学习率0.5带入公式，计算一下，由于这是第一次得到reward，没有任何之前的经验可以参考，因此所有的经验都为0，计算公式为：
$$q((3,2),exit)=(1-0.5)\ast 0.0+0.5[1+0.9\ast 0]=0.5$$
这样智能体的第一次冒险就结束了，只计算出一个终点时exit动作的Q Value。

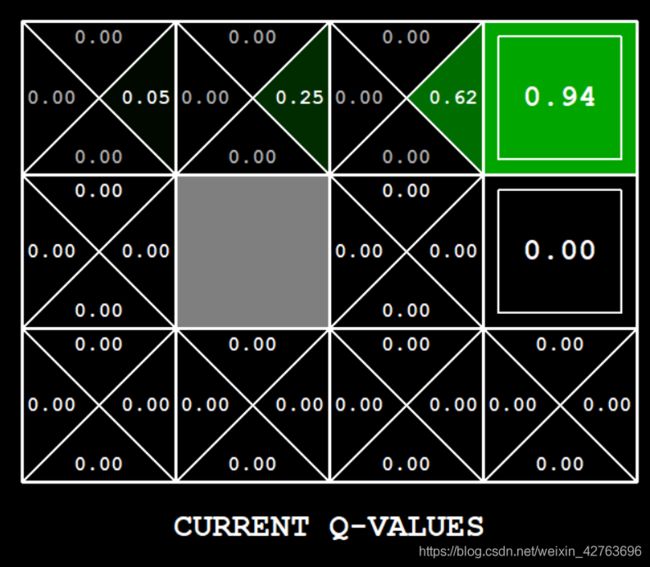
第二次让智能体走相同的路线，前几步由于reward值还是0，因此结果相同，直到倒数第二个格子(2,2)处

图6 刚进入(2,2)，还没有执行向右走的动作

图7 在(2,2)执行向右走的动作 可以看到在(2,2)的位置，向右的方向计算出了0.23，计算过程如下：

$$q((2,2),east)=(1-0.5)\ast 0.0+0.5[0.0+0.9\ast 0.5]=0.225$$
east就是向东、向右走，0.225经过四舍五入变成0.23，符合图7的结果。

在(3,2)处再执行exit动作后，结果为图8

图8 在(3,2)执行exit动作
计算过程如下

$$q((3,2),east)=(1-0.5)\ast 0.5+0.5[1+0.9\ast 0]=0.75$$

这样我们重复上述路径4次，最终得到图9的结果

图9 执行4次上述路径
注意：上述的过程都是由人类在执行动作，每一步都是确定的，因此可以定向地先往上走再往右走。真正强化学习的时候是由智能体自主行动，每个格子的action选择最佳值，但这样会出现问题，这会在4中讲到

4. 改进方法：Epsilon Greedy

上述的算法看上去可以在每次动作都选择到最佳的动作，但在使用上述算法让智能体去学习Grid World的时候，会遇到图10的问题：

图10 似乎有些不对劲？ 上述是迭代了好多次后智能体学会的最佳action选择，可以看到这个结果还是很有问题的，毕竟在第一行的时候，很明显朝右的方向是最佳选择，但学习出的都是朝上的方向，这里问题出在action的选择上。

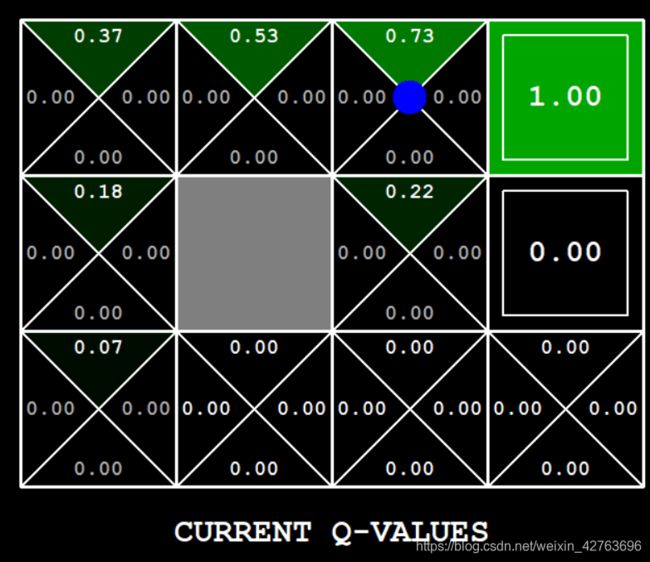
在Q Learning的方法中，我们选择每次reward最大的方向，这样就会陷入局部最优，即当向上的action的reward>0时，我就不会再去看别的方向的reward，即使向右走的reward要更大

这里的优化方法就是使用Epsilon Greedy，即以Epsilon的概率去选取reward最大的action，或者随机的action，代码如下：

r = random.random()
if r > epsilon:
	# 得到reward最大的action
	return computeActionFromQValues(state)
else:
	# 返回随机选择的合法action之一
	return random.choice(legalActions)

这样一来，学习到的结果就正常多了

图11 更符合直觉的结果

完结，撒花~

5. 参考资料

• 知乎回答：https://www.zhihu.com/question/26408259
• csdn博客：https://blog.csdn.net/itplus/article/details/9361915