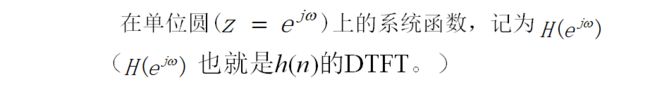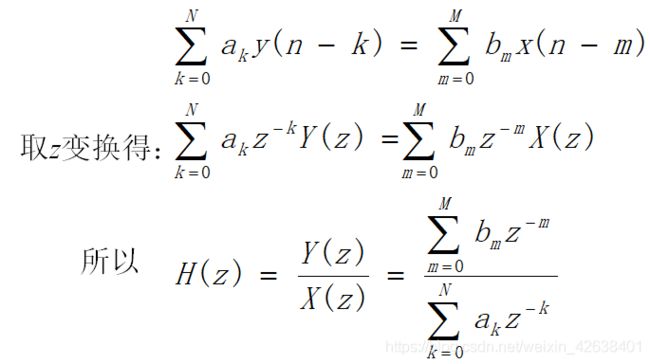离散系统的系统函数及系统的频率响应（2-8）

系统函数

 定义为：系统单位抽样响应h(n)的z变换，记为H(z) 

 

频率响应 

因果稳定系统 

1.稳定性：（由z变换分析稳定性） 

线性移不变系统稳定的充要条件：h(n)满足绝对可和 

即 ∑|h(n)|<∞

 

z变换H(z)的收敛域：满足 ∑|h(n)z-n|<∞ 的那些z 

如果收敛域包含单位圆，则有∑|h(n)|<∞ ，即系统稳定。

反过来说，稳定系统的收敛域应包括单位圆 |z| =1。 

2.因果性：（由z变换分析因果性）

LSI系统为因果系统的充要条件是单位抽样响应h(n)为因果序列，则其z变换H(z)的收敛域为 R-<|z|≤∞。

3.因果稳定系统的极点

收敛域 R-<|z|≤∞应包含单位圆 |z|=1，即系统函数收敛域至少为 1≤|z|≤∞； 

也就是说，其全部极点（z平面上对应于H(z)的表达式=∞的点）必须在单位圆内。

系统函数与差分方程的关系 

线性移不变系统常用差分方程表示：

可见，除了比例常数K以外，系统函数完全由它的零点、极点决定 

系统的频率响应的意义

系统的频率响应 

对于线性移不变系统：

输出序列的傅氏变换等于输入序列的傅氏变换与频率响应的乘积。

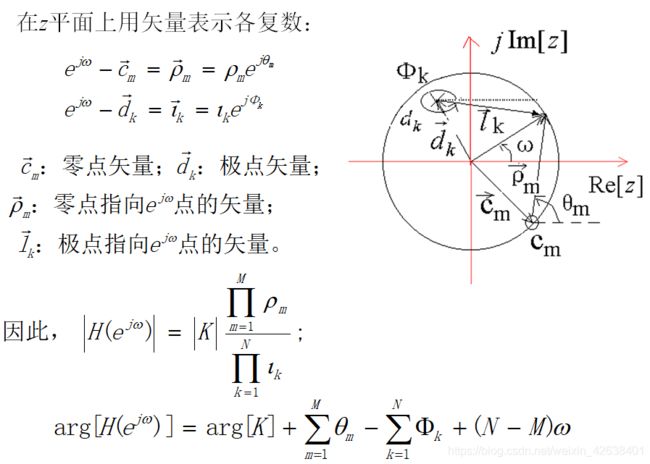
频率响应的几何确定

1.频率响应的零极点表达式

2.几点说明

(2) 单位圆附近的零点对幅度响应的谷点的位置与深度有明显影响，当零点位于单位圆上时，谷点为零。零点可在单位圆外。

(3) 单位圆附近的极点对幅度响应的峰点位置和高度有明显影响。极点在圆外，则系统不稳定。

IIR系统和FIR系统 

1.无限长单位冲激响应(IIR)系统 Infinite-duration Impulse Response

定义：如果系统的单位抽样响应h(n)延伸到无穷长,即n→∞时,h(n)仍有值,则称作IIR系统。 

2.有限长单位冲激响应(FIR)系统Finite-duration Impulse Response

定义： h(n)为有限长序列的系统。 

从系统结构上说，FIR系统的输出是输入的组合运算，没有输出端到输入端的反馈，可以用“非递归”结构实现；

     而IIR系统在求y(n)时需要用到以前的输出值y(n-k)，因此在结构上有输出到输入的反馈，是“递归型”结构。

3.几个概念

       FIR系统在有限z平面没有极点，称为全零点系统，也称为滑动平均 (moving average, MA)系统。

       对于IIR系统，当系统函数

的分子项只有常数时，有限z平面上就只有极点，称为全极点系统，也称自回归（Autoregressive, AR）系统。

      有限z平面上既有零点又有极点的系统，称为零极点系统，又称为自回归滑动平均（Autoregressive moving average，ARMA）系统。