生成模型详解

一、生成模型的定义

1. 给定的训练集$X=\{x^1,x^2,...,x^n\}$
2. 隐变量$z$满足$p(z)=\mathcal{N}(0,I)$
3. 定义一个条件分布$p_{\theta }(x|z)$，$\theta$可以理解为生成模型的参数
4. 训练好模型后，采样$z\sim p(z)$，利用$p_{\theta }(x|z)$可以生成$x$

注：$p_{\theta }(x|z)$可以理解为“生成器”，把高斯$z$映射到数据分布$x$

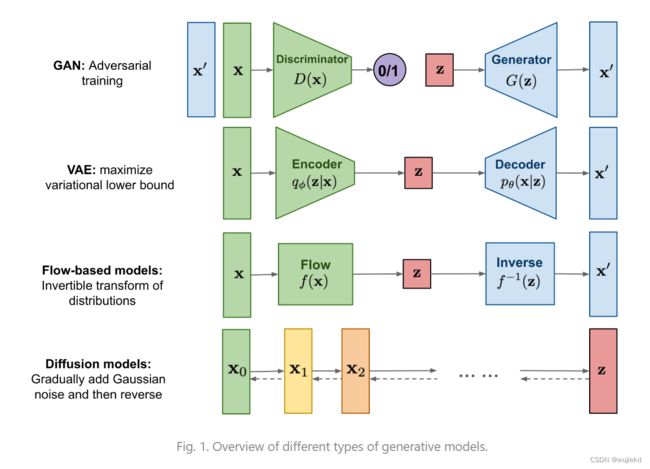
二、四种代表生成模型

1. VAE

注：Diffusion model的部分理论推导和VAE很相似

目的是能够得到真实数据的分布$p(x)$，这样就可以随意的生成数据。
借助隐变量$z$描述$x$的分布$p(x)$：$p(x)=\int p(x,z)dz=\int p(x|z)p(z)dz$

目标是最大化似然$p_{\theta }(x)$，$p_{\theta }(x)$ = $\frac{p_{\theta }(z,x)}{p_{\theta }(z|x)}$= $\frac{p_{\theta }(z)p_{\theta }(x|z)}{p_{\theta }(z|x)}$

但是$p_{\theta }(z|x)$是intractable的，通常我们都需要借助variational inference的技巧，采用$q_{\varphi }(z|x)$去近似它。

将最大化似然$p_{\theta }(x)$转化成使得 ELBO(变分下界)最大
模型似然$\log p_{\theta }(x)\ge ELBO$,
$ELBO={\mathbb{E}}_{z\sim q_{\varphi }(z|x)}[\log p_{\theta }(x|z)+\log p(z)-\log q_{\varphi }(z|x)]={\mathbb{E}}_{z\sim q_{\varphi }(z|x)}\log p_{\theta }(x|z)-D_{KL}(q_{\varphi }(z|x)||p(z))$

$p_{\theta }(x|z)$为decoder部分，$q_{\varphi }(z|x)$为encoder部分
模型的优化的loss为$L_{VAE}(\theta ,\varphi )=-ELBO=D_{KL}(q_{\varphi }(z|x)||p(z))-{\mathbb{E}}_{z\sim q_{\varphi }(z|x)}\log p_{\theta }(x|z)$

第一项为计算两个多元高斯分布的KL散度
第二项为重建误差（reconstruction error），因为正是给定下$z$生成真实数据的似然，对于一个给定的训练样本$x^i$，我们可以采用蒙特卡洛方法（Monte Carlo method）来估计这个数学期望，即从$q_{\varphi }(z|x^i)$多次采样来估计$-{\mathbb{E}}_{z\sim q_{\varphi }(z|x)}\log p_{\theta }(x^i|z)\approx -\frac{1}{L}{\sum }_{l=1}^L\log p_{\theta }(x^i|z^{(i,l)})$

2. GAN和Flow-based Model

GAN和Flow-based Model，都是只需要一个“生成器”，先采样高斯噪声，然后用“生成器”把这个高斯噪声映射到数据分布就可以，而且只关心生成。

但是GAN和Flow-based Model也有别的缺陷，比如GAN还需要额外训练判别器，这导致训练很困难；而Flow-based Model需要模型是可逆函数，不能随便用一个图像分类or分割领域的SOTA神经网络，这也导致模型表达能力受限。

3. Diffusion model

只需要训练“生成器”，训练目标函数简单，而且不需要训练别的网络（判别器/后验分布等），并且这个生成器没啥限制，可以随便选表达能力极强的神经网络。

前向和反向是两条马尔可夫链。

• 前向过程（加噪过程）
  1、前者通常是手工设计的，目的是将任何数据分布转换为简单的先验分布（例如，标准高斯）
  2、定义：$q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_t\mathcal{I})$
  原图$x_0$，通过不断的高斯采样噪声，得到$x_t$。当$t$趋近无穷，$x_T$得到的就是标准的高斯噪声，均值为0，方差为1。
  3、任意时刻的$x_t$能通过$x_0$和$\beta$表示，假设${\alpha }_t=1-{\beta }_t$，并且${\overline{\alpha }}_t={\prod }_{i=1}^T{\alpha }_i$，展开$x_t$可以得到：$x_t=\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}{\overline{z}}_t$

• 反向过程（去噪过程）
  1、利用$x_t$，使用一个深度学习模型（U-net，参数为$\theta$），去计算出$x_{t-1}$
  2、定义： $p_{\theta }(x_{t-1}|x_t)=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_t,t),{\sum }_{\theta }(x_t,t))$

• 推理过程
  最大化$p_{\theta }(x)$，求解和VAE类似，区别就是$x_0$到隐变量$z$的后验变成$x_0$到$x_{t-1}$的后验。和VAE的推导下界类似
  
  完全展开后，优化的目标为
  

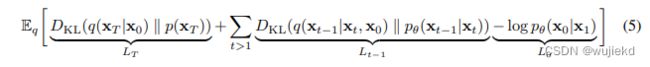
  其中由于$q(x_{t-1}|x_t,x_0)=q(x_t|x_{t-1},x_0)\frac{q(x_{t-1}|x_0)}{q(x_t|x_0)}$，可推导其分布如下：
  

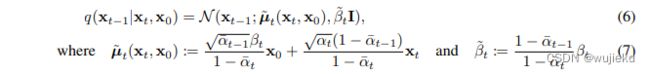
这个推导用于采样生成的噪声计算得到$x_{t-1}$的均值

再看一下优化的目标，没有参数的部分可以直接忽略，即$L_T$。而$L_{t-1}$根据多元高斯分布的KL散度求解等价于下面的式子

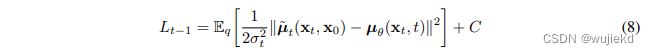
最后把式子(7)的均值代进(8)的左边，将$x_t$通过$x_0$进行表示，可得最终的优化目标

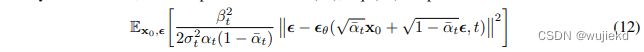
最后得到的简化后的loss如下：

可以理解为拉近每一时刻对应的前向和后向两个噪声分布。

• 训练过程和采样过程（生成数据）
  

上面是discrete model (DDPM) 最先提出的形式

下面是continuous model (SDE) 完善理论框架
首次揭示了diffusion model的连续版本对应的数学背景，并且将统计机器学习中的denoising score matching方法与DDPM中的去噪训练统一起来。