数理统计学导论(第8版)第七章充分性(Chapter7 Sufficiency) 知识小结、期末复习笔记 （待续

* 期末结束啦、把这学期的笔记分享一下、待续

* 参照英文版第8版数理统计学导论(Introduction to Mathematical Statistics, Eighth Editon)，Hogg，第7章 充分性；用了我自己的翻译

* 整个章节逻辑层次非常清晰, 定理概念之间层层递进、互相联系、补充，案例经典、方法明确且信息量大、仔细磨

7.1 估计量品质测量

① 极小方差无偏估计量(MVUE, Minimum Variance Unbiased Estimator)定义:

            有 的 , 若统计量 是无偏的，且 的方差 的任何其他无偏估计量的方差，那么称 为 的MVUE.

②决策函数(规则)：

           若 为 的点估计， 为 观测值的函数，函数 决定了 的点估计之值，从而称 为决策函数或决策规则(decision function/rule)，观测值 则为一个决策(decision).

 ③损失函数:

           非负数函数 定义为损失函数(loss function)，用于衡量 的真实值与其观测值 的差异程度. 损失函数的数学期望称为风险函数(risk function). 若 是 Y 的pdf, , 那么风险函数 由下式给出：

                       

            应用：极小化极大值准则(minimax criterion) : 使风险函数R的极大值取到极小值的决策函数L为最佳决策函数.      见书中举例.

            拓展：似然原理(likelihood principle)，见书中案例.

7.2 参数的充分统计量

④ 充分统计量(sufficient statistic)定义：

           设  是来自分布具有pdf或pmf为 的n个随机样本， ，设 是一个统计量，它的pdf或pmf是 ，于是 是 的充分统计量，当且仅当：

                                    

其中， 不依赖于 .

⑤ 求充分统计量的简便方法：奈曼因子分解定理：

            在④的条件下， 是 的充分统计量，当且仅当可以找出两个非负函数 , 使得：

             

其中 不依赖于 ； 为 构成的函数； 由 和   构成.  见书本举例.

  7.3 充分统计量的性质

⑥ 拉奥-布莱克韦尔(Rao-Blackwell)定理：

           由充分统计量 得到 (无偏化校正) 并表示 [即 ] 的无偏估计量为 的MVUE.

⑦ 的唯一的极大似然估计量 是充分统计量 的函数.

⑧ 补充： 的极大似然估计量是渐进无偏的.

求 的极小方差无偏估计量(MVUE)的方法：

1.  求出 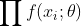, 得到一个充分估计量 ；-----------------根据⑤因子分解定理
2. 求 的极大似然估计量 ，注意到它是充分估计量 的函数，且是无偏的；---根据⑦
3. 求2中极大似然估计量 的数学期望(为 的函数)，依据数学期望将其校正为 的无偏估计量 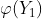，它就是 的MVUE.  ---------------根据⑥

 7.4 完备性与唯一性(Completeness and Uniqueness)

⑨ 完备族(complete family)的定义：

            对于连续或离散的随机变量Z，它拥有的pdf或pmf是 族的成员之一. 若要使条件 成立，需要 为0，除了在对每个   具有概率0的点集之外. 那么上述的族 就称为概率密度函数或质量函数的完备族.

⑩ 莱曼和谢弗(Lehmann and Scheffe)定理：

            由 pdf或pmf来自完备族 的充分统计量 得到并表示的无偏估计量为 的唯一的MVUE.

见书中的相关案例.

7.5 指数分布类(the Exponential Class of Distributions)

11                         

12 将形式为11的pdf称为概率密度函数或质量函数的正则指数类(regular exponential class)的一个成员，如果：

            Ⅰ X的支集不依赖于 .

            Ⅱ 是 的非平凡连续函数(nontrivial continuous function).

            Ⅲ 若X连续，则K'(x)0且H(x)是   的连续函数；若X离散，则K(x)是 的非平凡函数.

 13 记结论 (X来自正则指数族)：

            Ⅰ 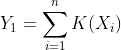  为参数 的充分统计量，其概率密度函数是完备的(定理7.5.2)

           Ⅱ   有如下形式的pdf或pmf：( ，且 依赖与于 .)

                                         

          Ⅲ                       

应用见书中例7.5.2，信息量大、重要！

待续

  分享    交流回复    指正