Classification methods 分类算法 （R）

写在前面

介绍了 6 种分类算法， 分别是 

Linear discriminant analysis （LDA），

Quadratic discriminant analysis （QDA），

Logistic regression (LR),

Support vector machines (SVM),

K-nearest neighbour (KNN).

为了介绍这五种算法是怎么操作的，我们会使用一个模拟数据的例子，先介绍算法的原理，再使用的R语言搭建模型，再判断模型的拟合程度，再对多个算法进行对比。

我写的初稿就是英文，所以这里就直接用英文了，也许后面会翻译一个中文版本。

Linear discriminant analysis （LDA）

Description of the method:

The LDA algorithm starts by finding directions that maximize the separation between classes, then use these directions to predict the class of individuals. These directions, called linear discriminants, are a linear combinations of predictor variables.

LDA assumes that predictors are normally distributed (Gaussian distribution) and that the different classes have class-specific means and equal variance/covariance.

Analysis and results:

Use function “lda()” in “MASS” to build the model based on trainSet, make prediction on testSet. The prediction provides “class”, which is the predicted classes of observation, use it to compute the confusion matrix.

We can find:

1. This model gives an accuracy rate 0.71 on testSet, which is barely good;
2. Sensitivity is 0.27 and Specificity is 0.89, Sensitivity is low;
3. Confusion matrix, of the 59 actual Group0 points, the system predicted that 43 were Group1, most of the points were misallocated. This is another way of showing Sensitivity (1-4359=0.27 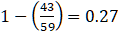). Of the 141 Group1 points, the system predicted that 15 were Group0, only a small part of points were misallocated. This is another way of showing Specificity (1-15141=0.89 ). Again we can say Specificity is good but Sensitivity is too low.

> model1 <- lda(Group ~ X1+X2, data = trainSet)
> prediction1 <- model1 %>% predict(testSet)
> confusionMatrix(as.factor(prediction1$class),as.factor(testSet$Group)) 
Confusion Matrix and Statistics

          Reference
Prediction   0   1
         0  16  15
         1  43 126
                                          
               Accuracy : 0.71            
                 95% CI : (0.6418, 0.7718)
    No Information Rate : 0.705           
    P-Value [Acc > NIR] : 0.4733208       
                                          
                  Kappa : 0.1912          
                                          
 Mcnemar's Test P-Value : 0.0003922       
                                          
            Sensitivity : 0.2712          
            Specificity : 0.8936          
         Pos Pred Value : 0.5161          
         Neg Pred Value : 0.7456          
             Prevalence : 0.2950          
         Detection Rate : 0.0800          
   Detection Prevalence : 0.1550          
      Balanced Accuracy : 0.5824          
                                          
       'Positive' Class : 0 

Quadratic discriminant analysis （QDA）

1. Briefly describe how the method works:

QDA is little bit more flexible than LDA, in the sense that it does not assumes the equality of variance/covariance. In other words, for QDA the covariance matrix can be different for each class.

LDA tends to be a better than QDA when we have a small training set.

1. Analysis and results:

Use function “qda ()” to build the model on trainSet and then make prediction on the testSet. The prediction provides “class”, which is the predicted classes of observation, use it to compute the confusion matrix.

We can see:

1. This model gives an accuracy rate 0.75 on the testSet, which is good;
2. Sensitivity is 0.42, Specificity is 0.88, overall better than LDA;
3. Confusion matrix, of the 59 actual Group0, the system predicted that 34 were Group1, over a half of the points were misallocated. And of the 141 Group1, the system predicted that 16 were Group0, a small part of the points were misallocated.

> model2 <- qda(Group ~ X1+X2, data = trainSet)
> prediction2 <- model2 %>% predict(testSet)
> confusionMatrix(as.factor(prediction2$class),as.factor(testSet$Group))
Confusion Matrix and Statistics



          Reference

Prediction   0   1

         0  25  16

         1  34 125

                                        

               Accuracy : 0.75          

                 95% CI : (0.684, 0.8084)

    No Information Rate : 0.705         

    P-Value [Acc > NIR] : 0.09230       

                                        

                  Kappa : 0.3405        

                                        

 Mcnemar's Test P-Value : 0.01621       

                                        

            Sensitivity : 0.4237        

            Specificity : 0.8865        

         Pos Pred Value : 0.6098        

         Neg Pred Value : 0.7862        

             Prevalence : 0.2950        

         Detection Rate : 0.1250        

   Detection Prevalence : 0.2050        

      Balanced Accuracy : 0.6551        

                                         

       'Positive' Class : 0   

 

Logistic regression (LR)

Logistic regression is used to predict the class (or category) of individuals based on one or multiple predictor variables (x). It is used to model a binary outcome, that is a variable, which can have only two possible values: 0 or 1, yes or no, diseased or non-diseased.

Logistic regression belongs to the GLM family, it does not return directly the class of observations. It allows us to estimate the probability (p) of class membership. The probability will range between 0 and 1. We need to decide the threshold probability at which the category flips from one to the other. By default, this is set to p = 0.5, but in reality it should be settled based on the analysis purpose.

 

Support vector machines (SVM)

Support Vector Machine is a machine learning technique used for classification tasks. Briefly, SVM works by identifying the optimal decision boundary that separates data points from different groups (or classes), and then predicts the class of new observations based on this separation boundary.

Depending on the situations, the different groups might be separable by a linear straight line or by a non-linear boundary line.

Support vector machine methods can handle both linear and non-linear class boundaries. It can be used for both two-class and multi-class classification problems.

In real life data, the separation boundary is generally nonlinear. Technically, the SVM algorithm perform a non-linear classification using what is called the kernel trick. The most commonly used kernel transformations are polynomial kernel and radial kernel.

 

K-nearest neighbour (KNN)

The rationale behind kNN is simple; the class label for a particular test point is the majority vote of the surrounding training data:

1. Compute the distance between test point and every training data point.
2. Find the k training points closest to the test point.
3. Assign test point the majority vote of their class label.

First scaling is not necessary here as X1  and X2  is numbers and on the same scale. Again we use “as.factor()” on the “Group” (two levels, 0 and 1). Then fit the model for various values of k (2 to 15). Then Finding optimal k using CV. Then make prediction on testSet and compute the confusion matrix.

 

# lassification
library(tidyverse)
library(MASS)
library(caret)
library(e1071)
library(verification)
library(pROC)
classification <- read.csv(".//R//XXX//Classification.csv", header = T)

#1. Summarise the two groups in terms of the variables X1 and X2. Describe your findings.
nrow(classification)
classification0 <- subset(classification, Group == 0)
classification1 <- subset(classification, Group == 1)
nrow(classification0) 
nrow(classification1) 
summary(classification0)
summary(classification1)
#group0 : gropu1 is nearly 3:7, more points in group 1,
#bigger range for group1 in both X1 and X2
#negative mean in both X1 and X2 for group0 , positive mean in both X1 and X2 for group1


#2. Select 80% of the data to act as a training set, with the remaining 20% for testing/evaluation.

set.seed(123)
setRandom800 <- sample(seq_len(1000), size = 800)
setRandom800
trainSet <- classification[setRandom800,]
testSet <- classification[-setRandom800,] 

#3.Perform classification using the following methods. 
#(a)Linear discriminant analysis.

#briefly describe how the method works
#http://www.sthda.com/english/articles/36-classification-methods-essentials/146-discriminant-analysis-essentials-in-r/
#Uses linear combinations of predictors to predict the class of a given observation. Assumes that the predictor variables (p) are normally distributed and the classes have identical variances (for univariate analysis, p = 1) or identical covariance matrices (for multivariate analysis, p > 1).

#present the results of an evaluation of the method and describe your findings. 
model1 <- lda(Group ~ X1+X2, data = trainSet)
prediction1 <- model1 %>% predict(testSet)
#this is the Model accuracy:
mean(prediction1$class==testSet$Group) #accuracy 0.71
confusionMatrix(as.factor(prediction1$class),as.factor(testSet$Group)) #confusionMatrix

confusionMatrix(as.factor(prediction1$class),as.factor(testSet.true$Group)) #confusionMatrix


#(b)b)  Quadratic discriminant analysis.
model2 <- qda(Group ~ X1+X2, data = trainSet)
prediction2 <- model2 %>% predict(testSet)
# Model accuracy
mean(prediction2$class == testSet$Group) #[1] 0.81
confusionMatrix(as.factor(prediction2$class),as.factor(testSet$Group)) #confusionMatrix

confusionMatrix(as.factor(prediction2$class),as.factor(testSet.true$Group)) #confusionMatrix


#(c) c) Logistic regression.
model3 <- glm(Group~.,family=binomial,data=trainSet)
a=predict(model3,newdata=testSet,type="response")
b=ifelse(a>0.5,1,0)
confusionMatrix(as.factor(b),as.factor(testSet$Group))

roc.plot(testSet$Group, a)
roc_obj <- roc(testSet$Group, a)
cutoff <- coords(roc_obj,x="best",input="threshold")
#cutoff <- coords(roc_obj,x="best",input="threshold", best.method = "youden")
cutoff
b=ifelse(a > 0.72,1,0)
confusionMatrix(as.factor(b),as.factor(testSet$Group)) 

confusionMatrix(as.factor(b),as.factor(testSet.true$Group)) #confusionMatrix


#(D)
## SVM with linear kernel ##
library(kernlab) 
trainSet.c <- trainSet
trainSet.c$Group <- as.factor(trainSet.c$Group)
testSet.c <- testSet
testSet.c$Group <- as.factor(testSet.c$Group)

mode4 <- train(
  Group ~., data = trainSet.c, method = "svmPoly",
  trControl = trainControl("cv", number = 10),
  tuneLength = 4
)

mode4$bestTune
predicted.classes <- mode4 %>% predict(testSet.c)
confusionMatrix(predicted.classes, testSet.c$Group) 

mode5 <- train(
  Group ~., data = trainSet.c, method = "svmRadial",
  trControl = trainControl("cv", number = 10),
  preProcess = c("center","scale"),
  tuneLength = 10
)
mode5$bestTune
# Make predictions on the test data
predicted.classes2 <- mode5 %>% predict(testSet.c)
confusionMatrix(predicted.classes2, testSet.c$Group) 

confusionMatrix(predicted.classes2,as.factor(testSet.true$Group)) #confusionMatrix


#(e)KNN
library(class)
library(ggplot2)

trainSet.c$Group
testSet.c$Group
train.X <- trainSet.c[,-3]
test.X <- testSet.c[,-3]
train.y <- trainSet.c[,3]
test.y <- testSet.c[,3]

opts <- trainControl(method='repeatedcv', number=5, repeats=10, p=0.7)
mdl <- train(x=train.X, y=train.y, # training data
             method='knn', # machine learning model
             trControl=opts, # training options
             tuneGrid=data.frame(k=seq(2, 15))) # range of k's to try
print(mdl)
# Test model on testing data
yTestPred <- predict(mdl, newdata=test.X)
confusionMatrix(yTestPred, test.y) # predicted/true

confusionMatrix(yTestPred,as.factor(testSet.true$Group)) #confusionMatrix



#5
trueDate <- read.csv(".//R//XXX//ClassificationTrue.csv", header = T)
classification$X1 == trueDate$X1
classification$Group == trueDate$Group

setRandom800
trainSet.true <- trueDate[setRandom800,]
testSet.true <- trueDate[-setRandom800,] 
testSet.true$X2 == testSet$X2
testSet.true$X1 == testSet$X1
testSet.true$Group == testSet$Group

confusionMatrix(as.factor(prediction1$class),as.factor(testSet.true$Group)) #confusionMatrix
confusionMatrix(as.factor(prediction2$class),as.factor(testSet.true$Group)) #confusionMatrix
confusionMatrix(as.factor(b),as.factor(testSet.true$Group)) #confusionMatrix
confusionMatrix(predicted.classes2,as.factor(testSet.true$Group)) #confusionMatrix
confusionMatrix(yTestPred,as.factor(testSet.true$Group)) #confusionMatrix