基于VS与OpenCV的模板匹配学习（2）：边缘匹配+图像金字塔

基于VS与OpenCV的模板匹配学习（2）

边缘模板匹配+图像金字塔

基于C++与OpenCV的模板匹配学习（1）OpenCV matchTemplate()示例

---

---

前言

在基于C++与OpenCV的模板匹配学习（1）OpenCV matchTemplate()示例中，以OpenCV库的内置函数matchTemplate()为例，展示了基于灰度值的模板匹配算法的效果。尽管算法在示例程序中，匹配效果良好。但在工程应用中，表现出两点缺陷。
（1）在光照条件发生变化时，基于灰度值的模板匹配算法表现较差。
（2）假定原图像像素点个数为m，模板图像像素点个数为n，模板匹配算法的时间复杂度为T(mn)，当原图像为2048*2048时，算法的运算时间较长。
为解决上述问题，鉴于图像的边缘很少受光线变化的影响这一光学特性，开始探究基于边缘/轮廓的模板匹配算法；此外，开始结合图像金字塔进行算法时间的优化。

---

一、边缘检测

这一部分主要讲解下面会用到的有关边缘模板匹配的一些相关知识。例如：常用canny、sobel算子。

1.1 边缘检测的一般步骤

滤波：边缘检测的算法基于图像强度的一阶和二阶导数，导数通常对噪声敏感，因此采用滤波器来改善边缘滤波器的性能。例如高斯滤波，利用高斯核对灰度矩阵加权求和。
增强：边缘增强基于确定图像各点领域强度的变化值，可计算梯度幅值。
检测：采用方法对增强图像的某些边缘点进行取舍，可通过阈值化方法。

1.2 sobel算子

sobel算子用于边缘检测的离散微分算子，结合高斯平滑和微分求导，计算灰度图像的近似梯度。在图像的任何一点使用sobel算子，可得到对应的梯度矢量。
sobel算子的计算过程：

• 在x和y方向求导：
  

• 近似梯度：
  

1.3 canny算子

canny边缘检测算子是John F.Canny于1986年开发的一个多级边缘检测算法，也是目前被很多人推崇为最优的边缘检测的算法。
canny边缘检测的步骤一般分为以下几步：
（1）消除噪声
高斯平滑滤波器，以下显示了size=5的高斯内核示例。

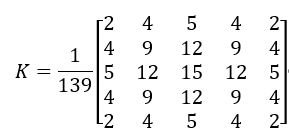
（2）计算梯度幅度与方向，参考sobel算子操作
（3）非极大值抑制
排除非边缘像素，仅仅保留了一些细线条。
（4）滞后阈值
canny使用了滞后阈值，滞后阈值需要两个阈值，高阈值与低阈值。阈值定义如下：
若某一像素的幅值高于高阈值，像素保留为边缘像素。
若某一像素的幅值低于低阈值，像素被排除。
若某一像素的阈值在高低阈值之间，且像素连接到一个边缘像素，该像素保留。
总结，canny设置高低阈值，会保留高于高阈值的像素点以及像素点周围一层像素点。

1.4 OpenCV sobel与canny函数

OpenCV有sobel算子与canny算子，这为我们进行边缘检测操作提供了便利。

sobel(InputArray src,OutArray dst,int ddepth,int dx,int dy,int ksize=3,double scale=1,double delta=0,int borderType=BORDER_DEFAULT)
(1)src、dst为Mat型的输入图像与输出图像
(2)ddepth为输出图像的深度，可理解为图像的位深。
(3)dx、dy为x和y方向上的差分阶数。
(4)ksize为Sobel核的大小，必须取奇数。
(5)sacle缩放因子，delta默认0，borderType边界模式。

canny(InputArray image,OutputArray edges,double threshold1,double threshold2,int apertyewSize=3,bool L2gradient=false)
(1)image、edges为Mat型的输入图像与输出图像
(2)threshold1、threshold2为高低阈值。
(3)apertyewSize表示应用Sobel算子孔径。
(4)L2gradient为计算图像梯度的标识。

1.5 OpenCV findContours函数

在后面的示例中，会使用到findContours()函数，因此先行讲解。在OpenCV，该函数从二值函数中查找轮廓。

findContours(InputArray image,OutputArray contours,OutputArray hierarchy,int mode,int method,Point offset)
(1)image为输入图像，图像的非零像素被视为1，0像素被保留为0，因此图像为二进制图像。
(2)contours为检测的轮廓，每个轮廓存储为一个点向量，用Point类型的vector表示。
(3)hierarchy包含图像的拓扑信息，每个轮廓contour[i]对应四个hierarchy元素hierarchy[i][0]-hierarchy[i][3],分别表示后一个轮廓，前一个轮廓，父轮廓，内嵌轮廓的索引编号。
(4)mode为轮廓检索模式，RETR_EXTERNAL为只检测最外层轮廓，RETR_LIST为检测所有轮廓并不建立等级关系，RETR_CCOMP检测所有轮廓并组织为双层结构，RETR_TREE检测所有轮廓并建立网状的轮廓结构。
(5)method为轮廓近似方法，CHAIN_APPROX_NONE获取每个轮廓的每个像素，CHAIN_APPROX_SIMPLE压缩水平和垂直方向，只保存方向的终点坐标。

二、边缘匹配算法

本文的边缘匹配算法思想源于印度小哥写的开源项目。
Edge Based Template Matching
当然，如果觉得印度小哥的代码不容易理解，这边建议参考。
edgebased_template_matching.cpp
本文参考的代码主要为edgebased_template_matching.cpp。
开源代码存在一些坑，已经成功调试与修改。
下面对代码进行详解。

2.1 图像读入

代码如下：

	Mat src = imread("D:/images/search2.jpg");
	Mat tpl = imread("D:/images/template.jpg");
	if (src.empty() || tpl.empty()) {
		printf("could not load images...\n");
		return -1;
	}

	namedWindow("source", WINDOW_AUTOSIZE);
	namedWindow("template", WINDOW_AUTOSIZE);
	imshow("source", src);
	imshow("template", tpl);

原图像和模板图像的读取，并分别显示。

2.2 模板轮廓点提取

代码如下：

	Mat gray, binary;
	cvtColor(tpl, gray, COLOR_BGR2GRAY);
	Canny(gray, binary, 100, 800);
	vector<vector<Point>> contours;
	vector<Vec4i> hireachy;
	findContours(binary, contours, hireachy, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE, Point(-1, -1));

cvtColor将原图像由彩图转化为灰度图；
Canny对图像进行边缘检测，将图像变为0-1图像。
findContours找出模板图像的轮廓点。

2.3 计算模板轮廓的dx,dy,mag,log

代码如下：

	Mat gx, gy;
	Sobel(gray, gx, CV_32F, 1, 0);
	Sobel(gray, gy, CV_32F, 0, 1);
	Mat magnitude, direction;
	cartToPolar(gx, gy, magnitude, direction);
	long contoursLength = 0;
	double magnitudeTemp = 0;
	int originx = contours[0][0].x;
	int originy = contours[0][0].y;
	// 提取dx\dy\mag\log信息
	vector<vector<ptin>> contoursInfo;
	// 提取相对坐标位置
	vector<vector<Point>> contoursRelative;
	// 开始提取
	for (int i = 0; i < contours.size(); i++) {
		int n = contours[i].size();
		contoursLength += n;
		contoursInfo.push_back(vector<ptin>(n));
		vector<Point> points(n);
		for (int j = 0; j < n; j++) {
			int x = contours[i][j].x;
			int y = contours[i][j].y;
			points[j].x = x - originx;
			points[j].y = y - originy;
			ptin pointInfo;
			pointInfo.DerivativeX = gx.at<float>(y, x);
			pointInfo.DerivativeY = gy.at<float>(y, x);
			magnitudeTemp = magnitude.at<float>(y, x);
			pointInfo.Magnitude = magnitudeTemp;
			if (magnitudeTemp != 0)
				pointInfo.MagnitudeN = 1 / magnitudeTemp;
			contoursInfo[i][j] = pointInfo;
		}
		contoursRelative.push_back(points);
	}

这一部分比较冗长，主要内容为计算模板图像每个轮廓点的x和y方向的导数以及幅度与相位。

2.4 计算原图像的dx,dy,mag,log

代码如下：

// 计算目标图像梯度
	Mat grayImage;
	cvtColor(src, grayImage, COLOR_BGR2GRAY);
	Mat gradx, grady;
	Sobel(grayImage, gradx, CV_32F, 1, 0);
	Sobel(grayImage, grady, CV_32F, 0, 1);
	Mat mag, angle;
	cartToPolar(gradx, grady, mag, angle);

计算原图像的每个像素点的x和y方向的导数以及幅度与相位。

2.5 最优匹配点寻找

代码如下：

	long totalLength = contoursLength;
	double nMinScore = minScore / totalLength; // normalized min score
	double nGreediness = (1 - greediness * minScore) / (1 - greediness) / totalLength;
	double partialScore = 0;
	double resultScore = 0;
	int resultX = 0;
	int resultY = 0;
	double start = (double)getTickCount();
	for (int row = 0; row < grayImage.rows; row++) {
		for (int col = 0; col < grayImage.cols; col++) {
			double sum = 0;
			long num = 0;
			for (int m = 0; m < contoursRelative.size(); m++) {
				for (int n = 0; n < contoursRelative[m].size(); n++) {
					num += 1;
					int curX = col + contoursRelative[m][n].x;
					int curY = row + contoursRelative[m][n].y;
					if (curX < 0 || curY < 0 || curX > grayImage.cols - 1 || curY > grayImage.rows - 1) {
						continue;
					}

					// 目标边缘梯度
					double sdx = gradx.at<float>(curY, curX);
					double sdy = grady.at<float>(curY, curX);

					// 模板边缘梯度
					double tdx = contoursInfo[m][n].DerivativeX;
					double tdy = contoursInfo[m][n].DerivativeY;

					// 计算匹配
					if ((sdy != 0 || sdx != 0) && (tdx != 0 || tdy != 0))
					{
						double nMagnitude = mag.at<float>(curY, curX);
						if (nMagnitude != 0)
							sum += (sdx * tdx + sdy * tdy) * contoursInfo[m][n].MagnitudeN / nMagnitude;
					}

					// 任意节点score之和必须大于最小阈值
					partialScore = sum / num;
					if (partialScore < min((minScore - 1) + (nGreediness * num), nMinScore * num))
						break;
				}
			}

			// 保存匹配起始点
			if (partialScore > resultScore)
			{
				resultScore = partialScore;
				resultX = col;
				resultY = row;
			}
		}
	}

这一部分是算法思想实现的核心部分，resultX与resultY用来保存最优匹配点的位置，resultScore用来保存最优匹配点的匹配分数。可以看到，该部分套用了四层循环，时间复杂度为原图像像素点数量与模板图像轮廓点数量的乘积。尽管代码设置了内循环的停止条件，这为代码运行速度带来了些许优化，但当原图像大小较长时，算法的运行时间依然很久。例如在我的场景下，原图像为2048*2048格式，算法运行时间为50s，在后一章结合图像金字塔进行时间的优化。

2.6 Bug调试

源代码存在一些Bug，已经解决并总结如下。

（1）canny参数设置不当：

Canny(gray, binary, 100, 800);

canny函数高阈值设定不当，会导致模板图像找不到轮廓点。建议如下修改：

Canny(gray, binary, 100, 200);

（2）模板轮廓点坐标为负数：
在特定场景，会出现轮廓点x或y坐标出现负数的情况，这会导致后续轮廓点作为数组索引坐标的时候，导致超出数组索引下限。

for (int i = 0; i < contours.size(); i++) {
		int n = contours[i].size();
		contoursLength += n;
		contoursInfo.push_back(vector<ptin>(n));
		vector<Point> points(n);
		for (int j = 0; j < n; j++) {
			int x = contours[i][j].x;
			int y = contours[i][j].y;
			points[j].x = x - originx;
			points[j].y = y - originy;
			ptin pointInfo;
			pointInfo.DerivativeX = gx.at<float>(y, x);
			pointInfo.DerivativeY = gy.at<float>(y, x);
			magnitudeTemp = magnitude.at<float>(y, x);
			pointInfo.Magnitude = magnitudeTemp;
			if (magnitudeTemp != 0)
				pointInfo.MagnitudeN = 1 / magnitudeTemp;
			contoursInfo[i][j] = pointInfo;
		}
		contoursRelative.push_back(points);
	}

解决如下：

for (int i = 0; i < contours.size(); i++) {
		int n = contours[i].size();
		contoursLength += n;
		contoursInfo.push_back(vector<ptin>(n));
		vector<Point> points(n);
		for (int j = 0; j < n; j++) {
			int x = contours[i][j].x;
			int y = contours[i][j].y;
			if (x < 0)x = 0;
			if (y < 0)y = 0;
			points[j].x = x - originx;
			points[j].y = y - originy;
			ptin pointInfo;
			pointInfo.DerivativeX = gx.at<float>(y, x);
			pointInfo.DerivativeY = gy.at<float>(y, x);
			magnitudeTemp = magnitude.at<float>(y, x);
			pointInfo.Magnitude = magnitudeTemp;
			if (magnitudeTemp != 0)
				pointInfo.MagnitudeN = 1 / magnitudeTemp;
			contoursInfo[i][j] = pointInfo;
		}
		contoursRelative.push_back(points);
	}

2.7 算法结果展示

在经过Bug调试后，在我的场景中，代码可以正常运行。输入模板图像与目标图像，匹配结果如下。

根据匹配结果可知，方形边框为结果匹配区域，不难发现，基于边缘梯度的模板匹配在匹配结果上表现良好。其实，可以在不同亮度值进行算法的性能测试，并与基于灰度值的模板匹配进行效率与精度的对比。这边缺乏用于测试的图像数据样本，所以考虑在后续学习中进行综合对比。

三、图像金字塔

上文提到，示例图像为2048*2048时，算法运行时间大概为50s。这是由于算法的时间复杂度为目标图像像素点*模板图像轮廓点，当目标图像像素点个数较高，往往也会导致模板图像的轮廓信息越丰富，因此当目标图像被压缩后，算法速度会得到显著提升。因此，本文考虑结合图像金字塔对算法时间进行优化，首先会介绍图像金字塔的基本原理，然后介绍算法实现与时间优化的结果。

3.1 图像金字塔基本原理

图像金字塔是图像中多尺度表达的一种，主要用于图像的分割。在应用中，图像金字塔最初用于机器视觉和图像压缩，一幅图像的金字塔是一系列以金字塔形状排列的，分辨率逐步降低且来源于同一张原始图的图像集合。金字塔的最底部是原始图像，顶部是低分辨率的近似。
图像金字塔包括高斯金字塔与拉普拉斯金字塔，前者用来向下采样图像，后者用来向上采样，可以对图像进行最大程度的还原，即重建图像。高斯金字塔是通过高斯平滑与亚采样获得一些下采样图像，也就是说第K层高斯金字塔通过平滑、亚采样就可以获得K+1层高斯图像。金字塔的图像如图所示。

3.2 OpenCV pyrDown函数

要从金字塔第i层生成第i+1层，我们先用高斯核进行卷积，然后删除所有的偶数行和偶数列，新得到图像面积会变为源图像的四分之一。对于高斯金字塔，当图像向金字塔的上层移动时，尺寸和分辨率会降低。在OpenCV中，可以通过pyrDown函数进行操作。
pyrDown函数的作用是向下采样并模糊一张图片。
pyrDown(InputArray src,OutputArray dst,const Size&dstSize=Size(),int borderType=BORDER_DEFAULT)
(1)src、dst为Mat型的输入图像与输出图像
(2)const Size&dstSize为输出图像的大小，有默认值Size()，默认情况下，Size((src.cols+1)/2,(src.rows+1)/2)来进行计算。

3.3 高斯金字塔具体实现

基于高斯金字塔，我们使用分层搜索策略：
（1）首先我们根据模板图像与目标图像，计算出需要使用的图像金字塔层数。金字塔层数设置，需要保证最上层目标物体的相关结构必须可辨别出。
（2）然后在最高层金字塔进行一次完整的匹配。高斯金字塔每增加一层，图像点数与模板点数都会减少4倍，每增加一层可以提速16倍，例如在金字塔第四层进行一次完整的匹配，计算次数与原始图像减少了4096倍。
（3）在高层搜索到的匹配结果映射到金字塔的下一层中，直接将匹配得到的匹配点坐标乘2。在下一层的搜索区域定为匹配结果周围的一个区域，一般为5乘5或者7乘7的矩阵区域。
（4）这个过程，直到找不到匹配对象或者到金字塔的最底层结束。

高斯金字塔函数如下所示：
输入源图像与金字塔层数，输出下采样结果图像。

cv::Mat paramidGaussImage(cv::Mat src, int paramidNums)
{
	int paramidCount = paramidNums;
	cv::Mat srcPre = src;
	cv::Mat srcTemp;
	while (paramidCount > 1)
	{
		cv::pyrDown(srcPre, srcTemp, cv::Size(srcPre.cols / 2, srcPre.rows / 2));
		srcPre = srcTemp;
		paramidCount--;
	}
	return srcPre;
}

搜索策略实现：
findMatchingPosition输入为当前层数的ROI区域，设置为7乘7的矩阵区域。
findMatchingPosition输出为匹配位置。

	int row_min = 0;
	int	row_max = src.rows;
	int col_min = 0;
	int col_max = src.cols;
	int resultX = 0, resultY = 0;
	cv::Mat srcPre, srcTemp, tplPre, tplTemp;

	for (int paramidPre = paramidNums; paramidPre >= 1; paramidPre--)
	{
		cv::Mat srcPre, tplPre;
		srcPre = paramidGaussImage(src, paramidPre);
		tplPre = paramidGaussImage(tpl, paramidPre);
		if (paramidPre - paramidNums == 0)
		{
			row_min = 0;
			row_max = srcPre.rows;
			col_min = 0;
			col_max = srcPre.cols;
		}
		paramidPoint = findMatchingPosition(srcPre, tplPre, row_min, row_max, col_min, col_max);
		resultX = paramidPoint.x;
		resultY = paramidPoint.y;
		row_min = resultY * 2 - 3;
		row_max = resultY * 2 + 4;
		col_min = resultX * 2 - 3;
		col_max = resultX * 2 + 4;
	}

3.4 图像金字塔优化结果

在本场景中，设置高斯金字塔层数为4层，ROI区域为7乘7。在源图像进行模板匹配的运行时间为50s，经过高斯金字塔的时间优化，结果如下所示。

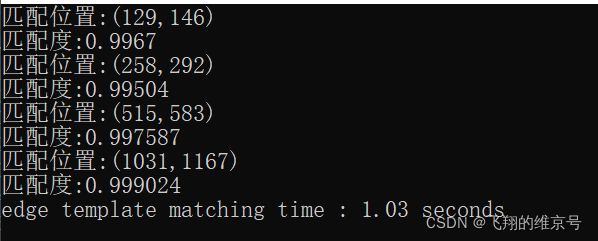
经过高斯金字塔的时间优化，算法运行速度优化到1s，尽管优化效果显著，但是1s的运行时间在大部分工业场景是不能接受的。因此，后续会进一步进行时间的优化。

---

参考文献：
《机器视觉算法及应用 Machine vision algorithm and Application》
《OpenCV3编程入门》 毛星云 著