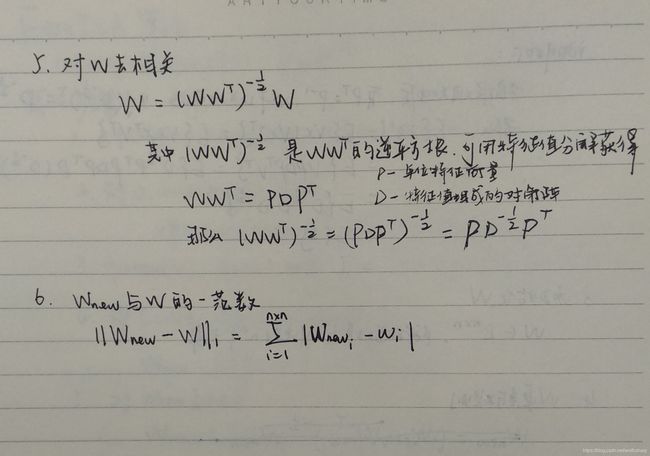FastICA算法的实现过程及其python实现
FastICA算法的数学原理及python实现
- ICA算法的数学原理
- 算法实现过程
- python实现
ICA算法的数学原理
参考我的这篇文章:ICA算法的数学原理
算法实现过程
python实现
(1)从硬盘中读取两段参数相同的语音信号S1和S2,大小都是(1,m)
(2)人为指定一个混合矩阵A,将S1和S2进行混合得到矩阵D,D的大小是(2,m)
(3)将混合的结果存入硬盘中:mix1.wav和mix2.wav
(4)对D作用FastICA算法,得到估算的源信号Sr,Sr的大小是(2,m)
(6)将估算的源信号存入硬盘中:reconsruct_sound1.wav和reconsruct_sound2.wav
完整代码:
#FastICA by Leo
import numpy as np
import math
import random
import matplotlib.pyplot as plt
'''
函数名称:center_data
函数功能:对数据中心化:对输入矩阵的每个元素,都减去该元素所在行(每一行一共有m个元素)的均值
输入参数:X 要处理的矩阵,大小为(n,m)
返回参数:X_center 进行中心化处理之后的矩阵,大小为(n,m)
作者:Leo Ma
时间:2020.01.04
'''
def center_data(X):
#沿着行的方向取均值,即计算n个麦克风在m个时刻中的均值,X_means的shape是(n,)
X_means = np.mean(X,axis = 1)
#将X_means增加一个新行,shape变为(n,1),X的每一列都与之对应相减
return X-X_means[:, np.newaxis]
'''
函数名称:whiten_data
函数功能:对数据白化处理
输入参数:X 要处理的矩阵,大小为(n,m)
返回参数:Z 白化处理之后的矩阵,大小为(n,m)
V 白化变换矩阵
作者:Leo Ma
时间:2020.01.04
'''
def whiten_data(X):
#计算X的协方差矩阵,cov_X = E{XX^T)}
cov_X = np.cov(X)
#计算协方差矩阵的特征值和特征向量
eigenValue,eigenVector = np.linalg.eig(cov_X)
#将特征值向量对角化,变成对角阵,然后取逆
eigenValue_inv = np.linalg.inv(np.diag(eigenValue))
#计算白化变换矩阵V
V = np.dot(np.sqrt(eigenValue_inv), np.transpose(eigenVector))
#计算白化处理后得矩阵Z,Z=VX
Z = np.dot(V,X)
return Z,V
'''
函数名称:gx
函数功能:定义s的CDF,这里选择tanh(),对输入矩阵的每个元素都作用tanh()
输入参数:x 要处理的矩阵,大小为(n,m)
alpha 常量,值域[1,2],通常取alpha=1
返回参数:gx tanh()的计算结果
作者:Leo Ma
时间:2020.01.04
'''
def gx(x,alpha=1):
return np.tanh(alpha*x)
'''
函数名称:div_gx
函数功能:定义s的pdf,tanh()的导数是1-tanh()**2
输入参数:x 要处理的矩阵,大小为(n,m)
alpha 常量,值域[1,2],通常取alpha=1
返回参数:div_gx tanh()导数的计算结果
作者:Leo Ma
时间:2020.01.04
'''
def div_gx(x,alpha=1):
return alpha*(1-gx(x)**2)
'''
函数名称:decorrelation_data
函数功能:对数据(W)进行去相关
输入参数:W 要处理的矩阵,大小为(n,n)
返回参数:W_decorrelation 去相关之后的W
作者:Leo Ma
时间:2020.01.04
'''
def decorrelation_data(W):
#对WW.T进行特征值分解,D是特征值,P是特征向量
D, P = np.linalg.eigh(np.dot(W, np.transpose(W)))
#特征值对角化,然后取逆
div_D = np.linalg.inv(np.diag(D))
#W_decorrelation = PD^(-1/2)P.T W
return np.dot(np.dot(np.dot(P,np.sqrt(div_D)), np.transpose(P)), W)
'''
函数名称:FastICA
函数功能:对输入矩阵做ICA处理
输入参数:Z 输入矩阵(观测矩阵中心化白化之后的结果),大小为(n,m)
返回参数:W ICA算法估计的W
iter_num ICA迭代次数
作者:Leo Ma
时间:2020.01.04
'''
def FastICA(Z):
n, m = Z.shape;
#create w,随机生成W的值
W = np.ones((n,n), np.float32)
for i in range(n):
for j in range(n):
W[i,j] = random.random()
#对W去相关
W = decorrelation_data(W)
#迭代compute W
maxIter = 200#设置最大迭代数量
for i in range(maxIter):
#计算当前S=WZ
S = np.dot(W,Z)
#计算当前S的gs和div_gs
gs = gx(S)
div_gs = div_gx(S)
#更新W
W_new = np.dot(gs, np.transpose(Z)) / float(m) - np.mean(div_gs, axis=1) * W
#对更新后的W去相关
W_new = decorrelation_data(W_new)
#计算更新前后W的一范数
diff = np.linalg.norm(W_new-W,1)
#更新W
W = W_new
#判断是否结束迭代
if diff < 0.00001:
break
return W,i+1
#应用方法
'''
函数名称:Jagged
函数功能:锯齿波生成器
输入参数:t 时刻
period 生成波形的周期
返回参数:jagged_value 与时刻t对应的锯齿波的值
作者:Leo Ma
时间:2020.01.04
'''
def Jagged(t, period = 4):
jagged_value = 0.5*(t-math.floor(t/period)*period)#math.floor(x)返回x的下舍整数
return jagged_value
'''
函数名称:create_data
函数功能:模拟生成原始数据
输入参数:None
返回参数:T 时间变量
S 源信号
D 观测到的混合信号
作者:Leo Ma
时间:2020.01.04
'''
def create_data():
#data number
m = 500
#生成时间变量
T = [0.1*xi for xi in range(m)]
#生成源信号
S = np.array([[math.sin(xi) for xi in T], [Jagged(xi) for xi in T]], np.float32)
#定义混合矩阵
A = np.array([[0.8, 0.2], [-0.3, -0.7]], np.float32)
#生成观测到的混合信号
D = np.dot(A, S)
return T, S, D
'''
函数名称:load_wav_data
函数功能:从文件中加载wav数据
输入参数:file_name 要读取的文件名
返回参数:T 时间变量
S 源信号
params wav数据参数
作者:Leo Ma
时间:2020.01.04
'''
def load_wav_data(file_name):
import wave
f = wave.open(file_name,'rb')
#获取音频的基本参数
params = f.getparams()
nchannels, sampwidth, framerate, nframes = params[:4]
#读取字符串格式的音频
strData = f.readframes(nframes)
#关闭文件
f.close()
#将字符串格式的音频转化为int类型
waveData = np.fromstring(strData,dtype=np.int16)
#将wave幅值归一化
S = waveData / (max(abs(waveData)))
T = np.arange(0,nframes) / framerate
return T,S,params
'''
函数名称:save_wav_data
函数功能:将wav数据保存到文件中
输入参数:file_name 要保存的文件名
params 保存参数
S wav信号
返回参数:None
作者:Leo Ma
时间:2020.01.04
'''
def save_wav_data(file_name,params,S):
import wave
import struct
outwave = wave.open(file_name, 'wb')
#设置参数
outwave.setparams((params))
#将信号幅值归一化
S = S / (max(abs(S)))
#逐帧写入文件
for v in S:
outwave.writeframes(struct.pack('h', int(v * 64000 / 2)))#S:16位,-32767~32767,注意不要溢出
outwave.close()
'''
函数名称:load_create_data
函数功能:从文件中加载wav数据,并对其进行混合
输入参数:None
返回参数:T 时间变量
S 源信号
D 观测到的混合信号
params wav数据的参数,两端音频参数是一样的
作者:Leo Ma
时间:2020.01.04
'''
def load_create_data():
#两段音频截取的一样长
T1,S1,params1 = load_wav_data('./voice/sound1.wav')
T2,S2,params2 = load_wav_data('./voice/sound2.wav')
if np.shape(T1)[0] > np.shape(T2)[0]:
T = T1
else:
T = T2
#将大小为(1,m)的S1、S2合并成S,S的大小为(2,m)
#其中S1[np.newaxis,:]将(m,)加入一个新轴,变成(1,m)
#np.vstack((a,b))将a和b两个矩阵在列方向上进行合并
#另外,np.hstack((a,b))将a和b两个矩阵在行方向上进行合并
S = np.vstack((S1[np.newaxis,:],S2[np.newaxis,:]))
#定义混合矩阵
A = np.array([[0.8, 0.2], [-0.3, -0.7]], np.float32)
#生成观测到的混合信号
D = np.dot(A, S)
return T,S,D,params1
'''
函数名称:show_data
函数功能:画出数据图
输入参数:None
返回参数:None
作者:Leo Ma
时间:2020.01.04
'''
def show_data(T, S):
plt.plot(T, S[0,:], color='r', marker="*")
plt.show()
plt.plot(T, S[1,:], color='b', marker="o")
plt.show()
#主函数入口
def main():
'''第一种创建数据方法:从文件中读取两端语音信号'''
#生成数据,T是时间变量,S是源信号,D是观测到的混合信号
T, S, D, params = load_create_data()
#将两段混合信号保存在硬盘上
save_wav_data('./voice/mix1.wav',params,D[0,:])
save_wav_data('./voice/mix2.wav',params,D[1,:])
'''第二种创建数据方法:用两个波形生成器生成两个信号'''
#T, S, D = create_data()
#对D进行中心化处理
D_center = center_data(D)
#对D_center进行白化处理
Z, V = whiten_data(D_center)
#对Z做FastICA算法处理
W,iter_num = FastICA(Z)
print("iter_num:")
print(iter_num)
#根据估计的W,重构原信号的估计Sr
Sr = np.dot(np.dot(W, V), D)
#将两段由FastICA算法重构的信号保存在硬盘上
save_wav_data('./voice/reconsruct_sound1.wav',params,Sr[0,:])
save_wav_data('./voice/reconsruct_sound2.wav',params,Sr[1,:])
#画出数据图像
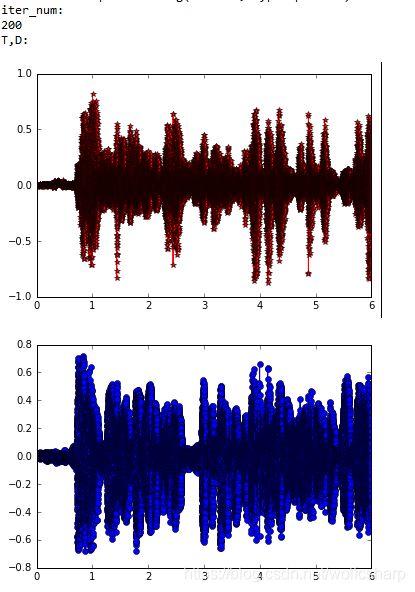
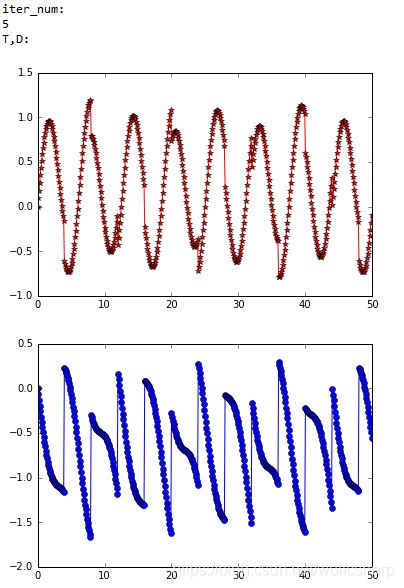
print("T,D:")
show_data(T, D)
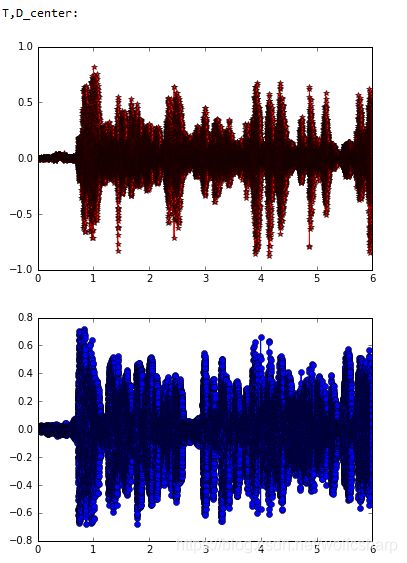
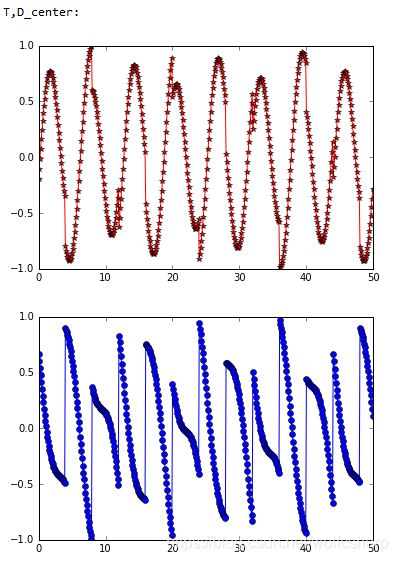
print("T,D_center:")
show_data(T, D_center)
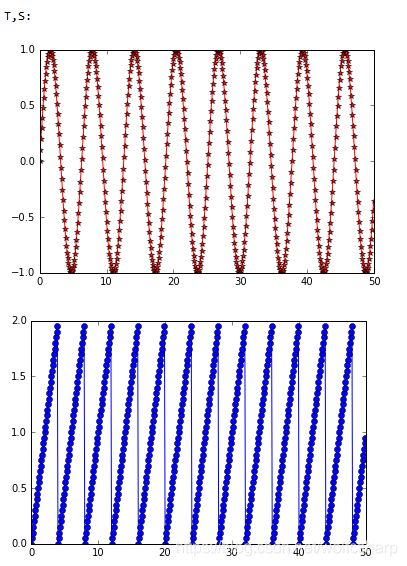
print("T,S:")
show_data(T, S)
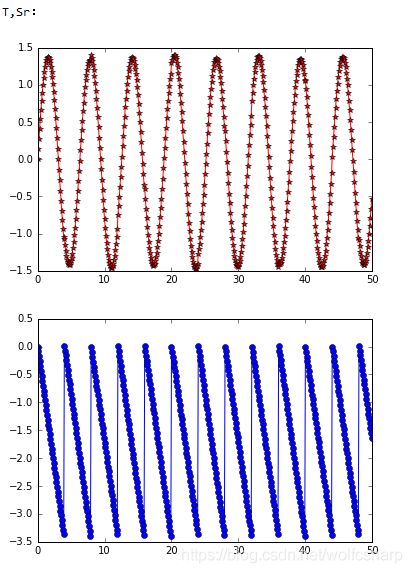
print("T,Sr:")
show_data(T, Sr)
if __name__ == "__main__":
main()
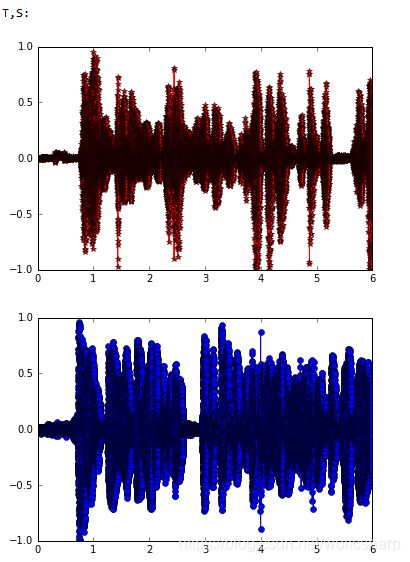
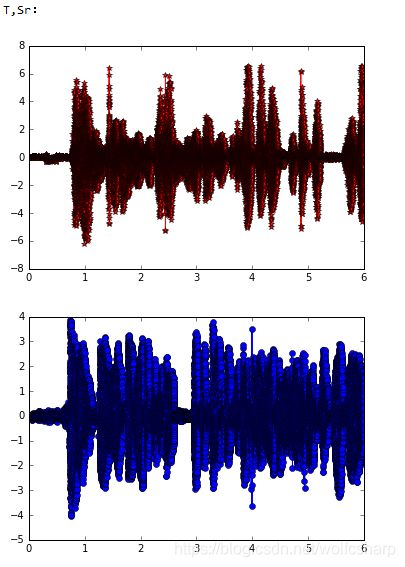
可以发现,通过图像对比效果不是特别明显,通过check硬盘中存储的声音信号,发现FastICA算法很好的将混合信号进行了分离: