深度学习笔记(十一)核对矩阵的维度(确定矩阵维度的精髓)
学习前面知识的过程中,遇到过很大的问题,那就是矩阵维度。这个到底是几乘几的矩阵?这个权重矩阵是否需要转置?输出的矩阵是否是我们期望的形状?那么这一课,我们来剖析一下参数及输入输出矩阵的维度。
一、参数 w [ l ] w^{[l]} w[l]和 b [ l ] b^{[l]} b[l]的维度
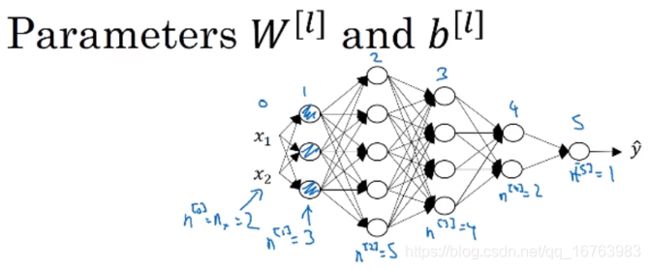
z [ 1 ] = w [ 1 ] x + b [ 1 ] z^{[1]}=w^{[1]}x+b^{[1]} z[1]=w[1]x+b[1]
考虑权重维度时,抛开偏置值进行分析。
z [ 1 ] : ( 3 , 1 ) , x : ( 2 , 1 ) ⇒ w [ 1 ] : ( 3 , 2 ) z^{[1]}:(3,1),x:(2,1)\Rightarrow w^{[1]}:(3,2) z[1]:(3,1),x:(2,1)⇒w[1]:(3,2)
b [ 1 ] : ( 3 , 1 ) b^{[1]}:(3,1) b[1]:(3,1)
z [ 2 ] = w [ 2 ] a [ 1 ] + b [ 2 ] z^{[2]}=w^{[2]}a^{[1]}+b^{[2]} z[2]=w[2]a[1]+b[2]
z [ 2 ] : ( 5 , 1 ) , a [ 2 ] : ( 3 , 1 ) ⇒ w [ 2 ] : ( 5 , 3 ) z^{[2]}:(5,1),a^{[2]}:(3,1)\Rightarrow w^{[2]}:(5,3) z[2]:(5,1),a[2]:(3,1)⇒w[2]:(5,3)
b [ 1 ] : ( 5 , 1 ) b^{[1]}:(5,1) b[1]:(5,1)
通过梳理如上两层网络,很容易得出以下结论:
z [ l ] , a [ l ] : ( n [ l ] , 1 ) z^{[l]},a^{[l]}:(n^{[l]},1) z[l],a[l]:(n[l],1)
w [ l ] : ( n [ l ] , n [ l − 1 ] ) w^{[l]}:(n^{[l]},n^{[l-1]}) w[l]:(n[l],n[l−1])
b [ l ] : ( n [ l ] , 1 ) b^{[l]}:(n^{[l]},1) b[l]:(n[l],1)
d w [ l ] : ( n [ l ] , n [ l − 1 ] ) dw^{[l]}:(n^{[l]},n^{[l-1]}) dw[l]:(n[l],n[l−1])
d b [ l ] : ( n [ l ] , 1 ) db^{[l]}:(n^{[l]},1) db[l]:(n[l],1)
二、向量化后的参数维度
抓住关键点,向量化即是将 m m m个训练样本 { x [ l ] ( 1 ) , x [ l ] ( 2 ) , . . . , x [ l ] ( m ) } \{x^{[l](1)},x^{[l](2)},...,x^{[l](m)}\} {x[l](1),x[l](2),...,x[l](m)}进行列堆积。那么输入向量 X : ( n [ 0 ] , m ) X:(n^{[0]},m) X:(n[0],m)
Z [ 1 ] = w [ 1 ] X + b [ 1 ] Z^{[1]}=w^{[1]}X+b^{[1]} Z[1]=w[1]X+b[1]
Z [ 1 ] : ( 3 , m ) , X : ( 2 , m ) ⇒ w [ 1 ] : ( 3 , 2 ) Z^{[1]}:(3,m),X:(2,m)\Rightarrow w^{[1]}:(3,2) Z[1]:(3,m),X:(2,m)⇒w[1]:(3,2)
b [ 1 ] : ( 3 , m ) b^{[1]}:(3,m) b[1]:(3,m)
Z [ 2 ] = w [ 2 ] A [ 1 ] + b [ 2 ] Z^{[2]}=w^{[2]}A^{[1]}+b^{[2]} Z[2]=w[2]A[1]+b[2]
Z [ 2 ] : ( 5 , m ) , A [ 1 ] : ( 3 , m ) ⇒ w [ 1 ] : ( 5 , 3 ) Z^{[2]}:(5,m),A^{[1]}:(3,m)\Rightarrow w^{[1]}:(5,3) Z[2]:(5,m),A[1]:(3,m)⇒w[1]:(5,3)
b [ 1 ] : ( 5 , m ) b^{[1]}:(5,m) b[1]:(5,m)
同样可以得出以下结论:
Z [ l ] , A [ l ] : ( n [ l ] , m ) Z^{[l]},A^{[l]}:(n^{[l]},m) Z[l],A[l]:(n[l],m)
w [ l ] : ( n [ l ] , n [ l − 1 ] ) w^{[l]}:(n^{[l]},n^{[l-1]}) w[l]:(n[l],n[l−1])
b [ l ] : ( n [ l ] , m ) b^{[l]}:(n^{[l]},m) b[l]:(n[l],m)
d w [ l ] : ( n [ l ] , n [ l − 1 ] ) dw^{[l]}:(n^{[l]},n^{[l-1]}) dw[l]:(n[l],n[l−1])
d b [ l ] : ( n [ l ] , m ) db^{[l]}:(n^{[l]},m) db[l]:(n[l],m)
通过整理矩阵中参数的维度,发现其实在运算过程中具有很强的规律性,而这样的一些积累,为我们编写代码时减少bug提供了很大的帮助,同时也提高了我们调试代码的效率。下次写神经网络代码时,不妨拿一张草稿纸出来,写写画画每一层网络参数的维度,以核对其正确性!
另外值得注意的是, A [ 0 ] = X : ( n [ 0 ] , m ) 或 ( n x , m ) , A [ l ] = y ^ : ( n [ l ] , m ) A^{[0]}=X:(n^{[0]},m)或(n_x,m),A^{[l]}=\widehat{y}:(n^{[l]},m) A[0]=X:(n[0],m)或(nx,m),A[l]=y :(n[l],m)