数学建模之时间序列的典型分解模型附Matlab代码
时间序列的典型分解模型
引言
一个时间序列的典型分解式为:
X t = m t + s t + Y t X_{t}=m_{t}+s_{t}+Y_{t} Xt=mt+st+Yt
其中 m t m_{t} mt为趋势项, s t s_{t} st是已知周期为d的周期项; Y t Y_{t} Yt是随机噪声项。
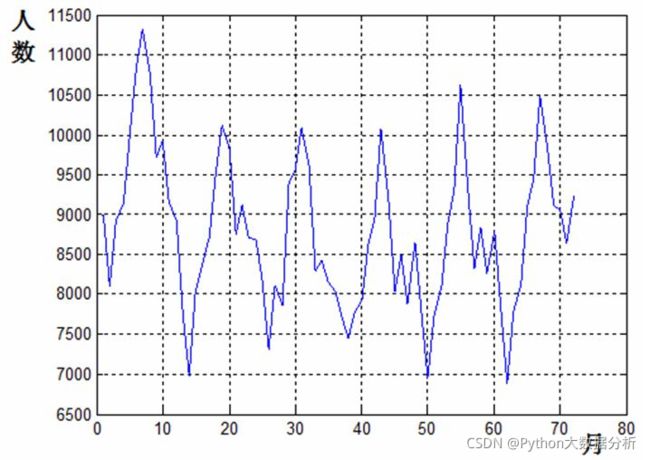
图1 某地6年交通死亡数据
计算过程
设某周期性数据为 X i j ( i = 1 , 2 , , n ; j = 1 , 2 , , 12 ) X_{i j}(i=1,2,,n;j=1,2,,12) Xij(i=1,2,,n;j=1,2,,12),共有n年数据,
每年有12个数据。现对未来12个月进行预测
(1)提取季节项
求出第 i 年平均值 X ˉ i = ∑ j = 1 12 X i j 12 ( i = 1 , 2 , … , n ) 对每个月数据零均值化 s t i j = X i j − X ˉ i ( i = 1 , 2 , … , n ; j = 1 , 2 , … , 12 ) 则季节项为: S j = ∑ i = 1 n s t i j n ( j = 1 , 2 , … , 12 ) \begin{array}{l} \text { 求出第 } i \text { 年平均值 } \bar{X}_{i}=\frac{\sum_{j=1}^{12} X_{i j}}{12}(i=1,2, \ldots, n)\\ \text { 对每个月数据零均值化 } s t_{i j}=X_{i j}-\bar{X}_{i} \quad(i=1,2, \ldots, n ; j=1,2, \ldots, 12)\\ \text { 则季节项为: } \quad S_{j}=\frac{\sum_{i=1}^{n} s t_{i j}}{n} \quad(j=1,2, \ldots, 12) \end{array} 求出第 i 年平均值 Xˉi=12∑j=112Xij(i=1,2,…,n) 对每个月数据零均值化 stij=Xij−Xˉi(i=1,2,…,n;j=1,2,…,12) 则季节项为: Sj=n∑i=1nstij(j=1,2,…,12)
该 S j S_{j} Sj即为季节项,这里T=12。满足
获取去掉季节项后数据
Y i j = X i j − S j ( i = 1 , 2 , , n ; j = 1 , 2 , , 12 ) Y_{i j}=X_{i j}-S_{j}(i=1,2,,n;j=1,2,,12) Yij=Xij−Sj(i=1,2,,n;j=1,2,,12)
将所有数据按行拉直变为一行令 Z = Y ˉ = ( Y 1 , 1 , Y 1 , 2 , . . . , Y 1 , 12 , Y 2 , 1 , Y 2 , 2 , . . . , Y 2 , 12 , Y n , 1 , Y n , 2 , . . . , Y n , 12 ) = ( z 1 , z 2 , . . . , z 12 n ) Z=\bar{Y}=(Y_{1,1},Y_{1,2},...,Y_{1,12},Y_{2,1},Y_{2,2},...,Y_{2,12},Y_{n,1},Y_{n,2},...,Y_{n,12})=(z_{1},z_{2},...,z_{12n}) Z=Yˉ=(Y1,1,Y1,2,...,Y1,12,Y2,1,Y2,2,...,Y2,12,Yn,1,Yn,2,...,Yn,12)=(z1,z2,...,z12n)
(3)回归拟合
对数据 z 1 , z 2 , . . . , z 12 n z_{1},z_{2},...,z_{12n} z1,z2,...,z12n.采用多项式回归拟合,如一次或二次多项式
如设回归结果为 z t = a + b . t ( t = 12 , … , 12 × n ) z_{t}=a+b.t(t=12,…,12×n) zt=a+b.t(t=12,…,12×n)
对消除季节项后未来12个月预测值为12+1,212+2…,212。即Yn+1,F7+12…,Y+12
则原始数据中未来12个月预测值为
(4)预测
对消除季节项后末来 12 个月预测值为 z ^ 12 n + 1 , z ^ 12 n + 2 , ⋯ , z ^ 12 n + 12 \hat{z}_{12 n+1}, \hat{z}_{12 n+2}, \cdots, \hat{z}_{12 n+12} z^12n+1,z^12n+2,⋯,z^12n+12 。 即 Y ^ n + 1 , 1 , Y ^ n + 1 , 2 , … , Y ^ n + 1 , 12 \hat{Y}_{n+1,1}, \hat{Y}_{n+1,2}, \ldots, \hat{Y}_{n+1,12} Y^n+1,1,Y^n+1,2,…,Y^n+1,12
则原始数据中末来 12 个月预测值为:
X ^ n + 1 , j = Y ^ n + 1 , j + S j ( j = 1 , 2 , … , 12 ) \hat{X}_{n+1, j}=\hat{Y}_{n+1, j}+S_{j} \quad(j=1,2, \ldots, 12) X^n+1,j=Y^n+1,j+Sj(j=1,2,…,12)
实例计算
根据某地6年每年12个月的交通死亡数据。 预测未来一年每个月的交通死亡人数。 数据见表一。
表1某地区交通死亡数据(1973年1月到1978年12月)
| 月份 | 1973 | 1974 | 1975 | 1976 | 1977 | 1978 |
|---|---|---|---|---|---|---|
| 1 | 9007 | 7750 | 8162 | 7717 | 7792 | 7836 |
| 2 | 8106 | 6981 | 7306 | 7461 | 6957 | 6892 |
| 3 | 8928 | 8038 | 8124 | 7776 | 7726 | 7791 |
| 4 | 9137 | 8422 | 7870 | 7925 | 8106 | 8129 |
| 5 | 10017 | 8714 | 9387 | 8634 | 8890 | 9115 |
| 6 | 10826 | 9512 | 9556 | 8945 | 9299 | 9434 |
| 7 | 11317 | 10120 | 10093 | 10078 | 10625 | 10484 |
| 8 | 10774 | 9823 | 9620 | 9197 | 9302 | 9827 |
| 9 | 9713 | 8743 | 8285 | 8037 | 8314 | 9110 |
| 10 | 9938 | 9129 | 8433 | 8488 | 8850 | 9070 |
| 11 | 9161 | 8710 | 8160 | 7874 | 8265 | 8633 |
| 12 | 8927 | 8680 | 8034 | 8467 | 8796 | 9240 |
Matlab程序
x=[9007,8106,8928,9137,10017,10826,11317,10744,9713,9938,9161,8927,...
7750,6981,8038,8422,8714,9512,10120,9823,8743,9129,8710,8680,...
8162,7306,8124,7870,9387,9556,10093,9620,8285,8433,8160,8034,...
7717,7461,7776,7925,8634,8945,10078,9179,8037,8488,7874,8647,...
7792,6957,7726,8106,8890,9299,10625,9302,8314,8850,8265,8796,...
7836,6892,7791,8129,9115,9434,10484,9827,9110,9070,8633,9240];
D=[9007,8106,8928,9137,10017,10826,11317,10744,9713,9938,9161,8927;
7750,6981,8038,8422,8714,9512,10120,9823,8743,9129,8710,8680;
8162,7306,8124,7870,9387,9556,10093,9620,8285,8433,8160,8034;
7717,7461,7776,7925,8634,8945,10078,9179,8037,8488,7874,8647;
7792,6957,7726,8106,8890,9299,10625,9302,8314,8850,8265,8796;
7836,6892,7791,8129,9115,9434,10484,9827,9110,9070,8633,9240];
aver=mean(D');
st=zeros(6,12);
for i=1:6
for j=1:12
st(i,j)=D(i,j)-aver(i);
end
end
NST=zeros(1,12);
nst=sum(st)/6; %对6年月平均作为st的估计
nx=zeros(72,1);
for i=1:6
for j=1:12
k=(i-1)*12+j; nx(k)=x(k)-nst(j);
end
end
%对消去季节项后数据nx
%进行线性拟合并预测
Y=zeros(72,1);
A=zeros(72,2);
for i=1:72
Y(i)=nx(i);
A(i,1)=1; A(i,2)=i;
end
coef=inv(A'*A)*A'*Y;
py=zeros(1,84);
for i=1:84
py(i)=coef(1)+coef(2)*i;
end
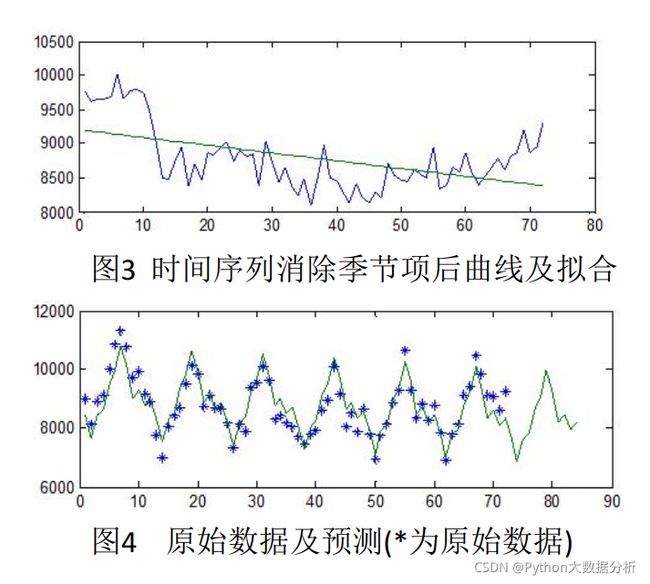
subplot(2,1,1);
plot(1:72,nx,1:72,py(1:72));
xx=zeros(1,84);
for i=1:7
for j=1:12
k=(i-1)*12+j;
xx(k)=py(k)+nst(j); %预测各月数值
end
end
subplot(2,1,2);
plot(1:72,x,'*',1:84,xx);