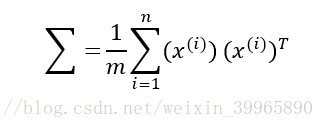K-means聚类与PCA【Coursera 斯坦福 机器学习】

本文基于Coursera 斯坦福吴恩达机器学习课程

谢绝任何不标记出处的转载

如有问题请联系作者

所有非手画图像（除公式）均来自课程

侵删

————————————————————————————————————————————————

1. 无监督学习简介 unsupervised learning

无监督学习相比监督学习，最大的差别就是没有用来衡量学习效果的手段（有无监督）。

例如在监督学习中，对于回归模型我们可以用观测值和估计值之差的平方和来衡量模型；对于分类问题我们可以用错误分类率来衡量。但在监督学习中，结果是未知的。举个例子，将5000份论文按照关键词进行学科分类，我们并不需要控制算法正确分类，而是让它自然而然通过学习进行归类，这就是一个无监督学习的例子。

2. 聚类

聚类是无监督学习的一种算法，它通过将拥有相似feature的量聚合进行归类。常见的聚类应用场景有：市场份额分割、社交网络分析、组织计算机集群帮助数据中心完成调度工作、天文数据分析等。

3. K-means 聚类

3.1 模型简介

K-means比较好用图像来说明。大致可以分为两类：数据点是明显可区分的（separated）和数据点是非分离的（non-separated）。

3.1.1 分离聚类（Separated clusters）

我们用一个只有两个簇（cluster）的K-means聚类来说明，如下图所示，

（1）最开始，我们用两个×（红色和蓝色两个类别）标记在任意位置（随机），计算每一个绿点（数据点）分别到两个×的距离，

（2）根据计算距离，我们将点归类到距离较小（离该×较近）的类别，然后分别计算所有红点坐标的均值，蓝点坐标的均值，

（3）这个计算的均值是我们新的分类点（cluster centroid），

重复（2）直到两个质心（centroid）不会再有大幅度变动。

3.1.2 非分离聚类（non-separated clusters）

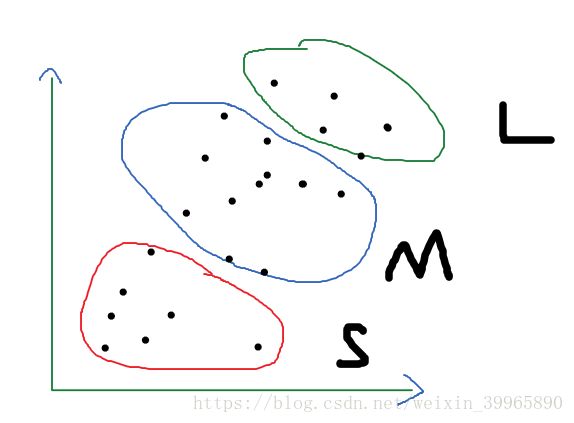
假设我们有以下身高体重的数据，想要把它们进行分类为SML三个型号，那么就可以使用K-means聚类。

3.2 关于cluster K的选取与最优解

K在建模的时候十分重要，关乎到模型类别。但是也不需要特别担心，如果最终结果里，没有一个数据点在类别ki里，删掉这个类就好了。这也说明，最终类别数量并不见得一定要与一开始的K一致。

对于K质心位置的选取，当类的数量K小于训练集集数m时，我们可以随机初始化K的质心，但我们很可能只能达到局部最优解。一个解决办法就是尝试多种（100种以上）随机初始化(random initialization)，选取cost function最小的那个。

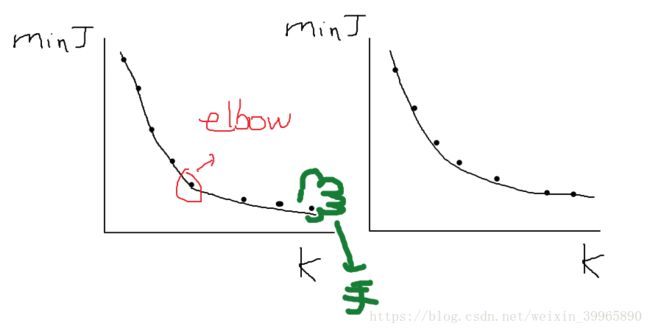
对于K数量的选取，一种不太有效的方法是Elbow method. 如下图所示。随着K的增加，cost function的最小值会逐渐减小。会在左图红圈处出现一个相对平衡的解（优化能力不错，也不会太多类太浪费）。但现实中我们的elbow 图往往是右图所示，所以这个方法不太理想。

不过这也为我们提供了一种检验K是否陷入局部最优解的方法，如果大K的cost function大于小K的，可能是大K陷入了一个局部最优解，我们需要重新设置random initialization来寻求大K的解。

对于K数量的选取，更多时候我们需要结合聚类在现实生活中的目的来选择。例如我们想要将5000篇论文分为三个学科，可能就需要选3-6个K来确保它至少是三个类。

3.3 目标函数的优化

对于K-means clustering，我们有如下目标函数。我们的目标是最小化J。该cost function J也被称作Distortion function. 

从3.1.1 的步骤我们就可以看出，k-means 其实已经在进行J的最小化了：使用平均数求取质心、不断改变质心的过程就是在缩小x与质心的距离。也是因为这个原因，K-means下的cost function J是不可能增大的，它只会减小。如果曲线不是单调递减，说明代码有问题。

4. Dimensionality Reduction and PCA

4.1  Why dimensionality Reduction

4.1.1 Data Compression 数据压缩

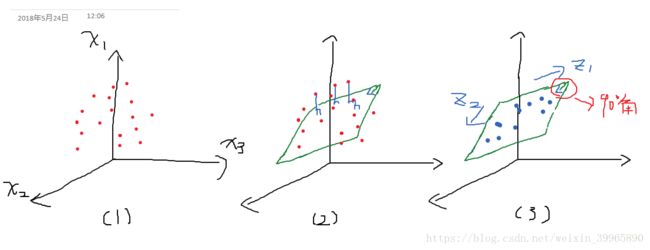
数据压缩就是采用映射的方法给数据降维。举一个例子，如下图所示，我们想要把一个三维数据组(x1, x2, x3)降维到一维。首先将3D坐标轴上的点投影到基向量为z1和z2单位向量的二维平面上，注意这个平面应该是矩形的。

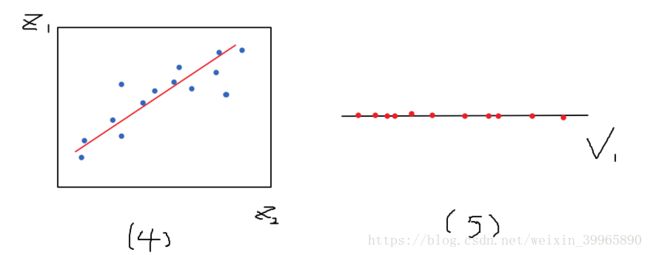
然后我们得到了如下（4）所示平面（注意这只是个巧合，并不是所有投影都能变成线性模型的形状）。将该2D数据投影到红线（v1），我们就可以得到一个一维的数据组（5）。

4.1.2 数据可视化

降维利于做数据可视化，可以把高维度的数据降维到2D-3D。但是对feature的解释就会变得比较麻烦了，基本全部变成了多重比例。

4.2 Principal Component Analysis（PCA） 

4.2.1 Problem Formulation

PCA是无监督学习的一种算法，用于降维和可视化。通过寻找合适的向量，将投影的误差降到尽可能低。举个例子，在做监督学习时，features过多可以用PCA先降个维。对于新features的定义，我们应该在训练集完成；但是测试集和CV集也可以应用PCA。这里需要注意的是，对于降维，PCA只有在原数据无法很好拟合的时候再用，不要一上来就PCA.

这里需要注意以下2D到1D的PCA和线性回归的区别。从目的上讲，线性回归是为了更好地预测未知数据，PCA只是为了降维。从手法上，线性回归的拟合是通过给定数据集使用最小二乘等方法求解，在解释变量中不同的变量有不同的权重，而PCA就是投影，所有的变量都一视同仁。

PCA不可以用来防止过拟合！过拟合应该用正则化处理。

4.2.2 PCA算法概述

在使用PCA算法前，因为每个feature的范围都不一样，我们要对数据做预处理。简单来说就是每个数减均值（mean normalization）或者一般的feature scaling（减均值除以标准差）。然后计算n*n协方差矩阵（covariance matrix）：

计算协方差矩阵的特征向量（eigenvectors）。对于特征向量的理解，这里提供CSDN博主“会敲键盘的猩猩”的一篇文章：《特征值和特征向量》（https://blog.csdn.net/u010182633/article/details/45921929）。

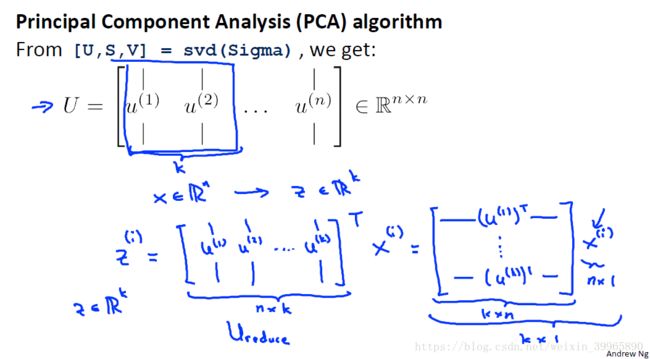
在matlab里我们用svd() 或 eig()计算（前者居多）。我们需要的是svd()的返回值U matrix。我们取U matrix的前k列作为需要降到的维度，即z matrix。 将z转置乘以X matrix，就成为了新的k*n features。 

下面来看一个例子。对于2D数据x1, x2降维，我们使用PCA，得到右下角一维数据。

4.2.3 对于维度K的选择

对于一组n维的数据，我们要将其降维到K维。K也被称为the number of principal components。我们依然使用最小化cost function的思想来做。投射错误均方很好理解，total variation in the data则意味着我们的数据距离0的距离。

在满足如下条件后，我们选择最小的k。 下式意味着"99% of variance is retained"。除了0.01，常用的还有0.05.

对于给定k, 我们通过计算上式是否符合小于0.01条件来判断其是否合适。但是这是一个非常没有效率的方法，在matlab种，我们用下图右边的S矩阵。