c++ 向量的值逆序输出_c++ 知道旋转前后矩阵向量值 求旋转矩阵c++/c#代码

原文作者：aircraft

知道旋转前后矩阵向量值 如何去求旋转矩阵R 的c++/c#代码？？？

因为需要用到矩阵处理库所以需要先配置

一、Eigen库的配置(VS2017)

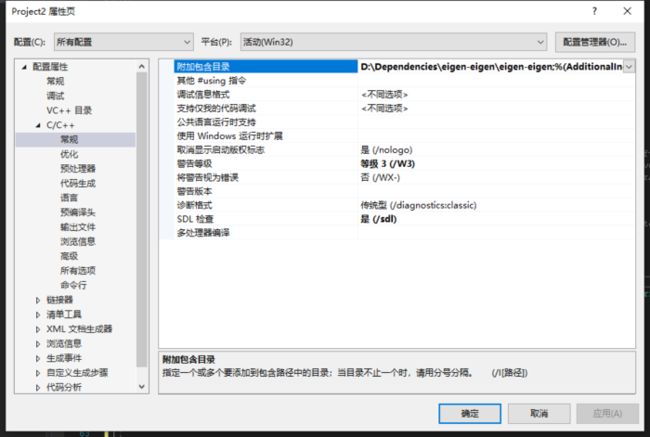
然后在自己的VS工程属性中的这个附加包含进去

注意看清楚了 是D:\Dependencies\eigen-eigen\eigen-eigen;      前面部分是你们自己的路径 后面的这个eigen-eigen\eigen-eigen; 代表的意思解压是点击进去选择里面那个名字跟外面一样的

二、实现代码

#include #include#include"Eigen/Dense"#include"Eigen/LU"#include"Eigen/Core"

#define PI 3.1415926

double calculateAngle(const Eigen::Vector3d &vectorBefore, const Eigen::Vector3d &vectorAfter)

{doubleab, a1, b1, cosr;

ab= vectorBefore.x()*vectorAfter.x() + vectorBefore.y()*vectorAfter.y() + vectorBefore.z()*vectorAfter.z();

a1= sqrt(vectorBefore.x()*vectorBefore.x() + vectorBefore.y()*vectorBefore.y() + vectorBefore.z()*vectorBefore.z());

b1= sqrt(vectorAfter.x()*vectorAfter.x() + vectorAfter.y()*vectorAfter.y() + vectorAfter.z()*vectorAfter.z());

cosr= ab / a1 /b1;return (acos(cosr) * 180 /PI);

}

inline Eigen::Vector3d calculateRotAxis(const Eigen::Vector3d &vectorBefore, const Eigen::Vector3d &vectorAfter)

{return Eigen::Vector3d(vectorBefore.y()*vectorAfter.z() - vectorBefore.z()*vectorAfter.y(), \

vectorBefore.z()*vectorAfter.y() - vectorBefore.x()*vectorAfter.z(), \

vectorBefore.x()*vectorAfter.y() - vectorBefore.y()*vectorAfter.x());

}void rotationMatrix(const Eigen::Vector3d &vectorBefore, const Eigen::Vector3d &vectorAfter, Eigen::Matrix3d &rotMatrix)

{

Eigen::Vector3d vector=calculateRotAxis(vectorBefore, vectorAfter);double angle =calculateAngle(vectorBefore, vectorAfter);

Eigen::AngleAxisd rotationVector(angle, vector.normalized());

Eigen::Matrix3d rotationMatrix=Eigen::Matrix3d::Identity();

rotMatrix= rotationVector.toRotationMatrix();//所求旋转矩阵

}intmain()

{

Eigen::Matrix3d rotMatrix;

Eigen::Vector3d vectorBefore(0,0,1);

Eigen::Vector3d vectorAfter(1,0,0);

rotationMatrix(vectorBefore, vectorAfter, rotMatrix);

std::cout<< rotMatrix <<:endl>

system("pause");return 0;

}

三、实现原理

1.旋转角度

已知旋转前向量为P, 旋转后变为Q。由点积定义可知：

可推出P，Q之间的夹角为：

2. 旋转轴

由1中可知，旋转角所在的平面为有P和Q所构成的平面，那么旋转轴必垂直该平面。

假定旋转前向量为a(a1, a2, a3)， 旋转后向量为b(b1, b2, b3)。由叉乘定义得：

所以旋转轴c(c1, c2, c3)为：

3.  罗德里格旋转公式(Rodrigues' rotation formula)

3.1 公式

已知单位向量 ， 将它旋转θ角。由罗德里格旋转公式，可知对应的旋转矩阵 ：

其中I是3x3的单位矩阵，

是叉乘中的反对称矩阵r：

3.2 公式证明

假设在坐标系(x, y, z)中，向量v=ax+by+cz，v绕z轴逆时针旋转θ角后得到新的向量v’。

根据2维(x,y)面上的旋转公式可得：

推出：

已知：

将上式带入v’的公式：

  将cz替换掉，可得：

将上式中的叉乘表示为反对称矩阵得：

另外：

最终可以推出：

上式即为罗德里格旋转公式。

参考博客里的是c#的实现代码

我是参考完之后改了一个c++的版本出来

若有兴趣交流分享技术，可关注本人公众号，里面会不定期的分享各种编程教程，和共享源码，诸如研究分享关于c/c++,python,前端，后端，opencv,halcon,opengl,机器学习深度学习之类有关于基础编程，图像处理和机器视觉开发的知识