【Pytorch】Pytorch学习笔记01
一、准备工作
官网:https://pytorch.org
中文文档:https://pytorch.apachecn.org/#/docs/1.7/
动手学深度学习:http://zh.d2l.ai/
安装pytorch

安装torchviz
安装graphviz软件(安装到系统变量)
https://graphviz.org/download/
安装torchviz库
pip install torchviz
二、基本概念
1、tensor张量
张量的使用和Numpy中的ndarrays很类似, 区别在于张量可以在GPU或其它专用硬件上运行, 这样可以得到更快的加速效果。
import torch
import numpy as np
data = [[1, 2], [3, 4]]
x_data = torch.tensor(data) # 张量
np_array = np.array(data) # ndarrays
x_np = torch.from_numpy(np_array) # 张量
Tensor的基础属性
requires_grad表示该tensor是否支持梯度计算。如果.requires_grad为 True,那么它会追踪该tensor的所有计算操作。
grad记录该tensor的梯度。在tensor完成计算后,调用.backward()计算出所有梯度,同时累加到.grad属性中。
grad_fn会记录作用在该tensor上的计算Function。如果该tensor是用户创建而非通过运算得出的,该tensor的.grad_fn就是None。
is_leaf,如果一个tensor是用户创建而非用过运算得出,那么该tensor在无环图中就是一个叶子节点,.is_leaf=True。引进叶子节点概念的目的:是为了节约内存,在反向传播结束后,非叶子节点的梯度默认会被释放掉,不会记录。

2、AutoGrad(自动求导/梯度)
PyTorch 反向传播的计算主要是通过autograd类实现了自动微分功能,而autograd 的基础是:
- 数学基础:复合函数,链式求导法则和雅克比矩阵;
- 工程基础 :Tensor 构成的计算图(DAG有向无环图);
在PyTorch 中是使用backward函数进行反向求导,当调用.backward()时,Autograd 将计算这些梯度并将其存储在各个张量的.grad属性中。
def backward(self, gradient=None,...)
backward 方法根据gradient参数的不同有2种可能:
- 如果gradient 是标量scale,直接计算完整的雅克比矩阵。如果缺省则使用默认值 1,即 backward(torch.tensor(1.))。
- 如果 gradient 是向量 vector。PyTorch 不会显式构造整个雅可比矩阵(实际的梯度),而是直接计算 Jacobian 乘积,这通常更简单有效,而且存储真正的梯度会浪费大量空间。
backward方法最终调用的是torch.autograd。torch.autograd是 PyTorch 的自动差分引擎,可为神经网络训练提供支持。torch.autograd从数学来说就是一个雅可比向量积计算引擎。
2.1 链式求导
2.2 方向导数
如果函数z=f(x, y)在点P(x,y)是可微分的,那么函数在该点沿任一方向的方向导数都存在,方向导数为: ∂ f ∂ l = ∂ f ∂ x cos φ + ∂ f ∂ y sin φ \frac{\partial f}{\partial l}=\frac{\partial f}{\partial x} \cos \varphi+\frac{\partial f}{\partial y} \sin \varphi ∂l∂f=∂x∂fcosφ+∂y∂fsinφ其中φ为x轴到方向l的转角。
2.3 梯度
梯度是一个向量,表示某一函数在该点处的方向导数沿着该方向取的最大值,即函数在该点处沿着该方向变化最快,变化率最大(即该梯度向量的模);当函数为一维函数的时候,梯度其实就是导数。
设函数z=f(x, y)在平面区域D内具有一阶连续偏导数, 则对于每一点 ( x , y ) ∈ D (x, y) \in D (x,y)∈D, 都可定义一个向量:
∂ f ∂ x i + ∂ f ∂ y j \frac{\partial f}{\partial x} i+\frac{\partial f}{\partial y} j ∂x∂fi+∂y∂fj
这向量称为函数 z=(x, y) 在点 P(x, y) 的梯度, 记作 grad f ( x , y ) \operatorname{grad} f(x, y) gradf(x,y) , 即 grad f ( x , y ) = ∂ f ∂ x i + ∂ f ∂ y j \operatorname{grad} f(x, y)=\frac{\partial f}{\partial x} i+\frac{\partial f}{\partial y} j gradf(x,y)=∂x∂fi+∂y∂fj
函数在某点的梯度是这样一个向量, 它的方向与取得最大方向导数的方向一致, 而它的模为方向导数的最大值. 由梯度的定义可知, 梯度的模为:
∣ grad f ( x , y ) ∣ = ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 |\operatorname{grad}f(x, y)|=\sqrt{\left(\frac{\partial f}{\partial x}\right)^{2}+\left(\frac{\partial f}{\partial y}\right)^{2}} ∣gradf(x,y)∣=(∂x∂f)2+(∂y∂f)2
2.4 雅可比向量积(Jacobian vector product)
在数学上,如果你有一个向量值函数 y ⃗ = f ( x ⃗ ) \vec{y}=f(\vec{x}) y=f(x),那么梯度 y ⃗ \vec{y} y 关于 x ⃗ \vec{x} x的梯度是一个雅可比矩阵 J J J,雅可比矩阵 J J J包含以下所有偏导组合:
J = [ ∂ f ∂ x 1 … ∂ f ∂ x n ] = ( ∂ f 1 ∂ x 1 ⋯ ∂ f 1 ∂ x n ⋮ ⋱ ⋮ ∂ f m ∂ x 1 ⋯ ∂ f m ∂ x n ) J=\left[\frac{\partial f}{\partial x_{1}} \ldots \frac{\partial f}{\partial x_{n}}\right]=\left(\begin{array}{ccc} \frac{\partial f_{1}}{\partial x_{1}} & \cdots & \frac{\partial f_{1}}{\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_{m}}{\partial x_{1}} & \cdots & \frac{\partial f_{m}}{\partial x_{n}} \end{array}\right) J=[∂x1∂f…∂xn∂f]= ∂x1∂f1⋮∂x1∂fm⋯⋱⋯∂xn∂f1⋮∂xn∂fm
我们假设如下:一个启用梯度的张量 X X X, X = [ x 1 , x 2 , … , x n ] X=\left[x_{1}, x_{2}, \ldots, x_{n}\right] X=[x1,x2,…,xn],假设这是杲个机橾学习模型的权 值。 X X X经过一些运算形成一个向量 Y Y Y, Y = f ( X ) = [ y 1 , y 2 , … , y m ] Y=f(X)=\left[y_{1}, y_{2}, \ldots, y_{m}\right] Y=f(X)=[y1,y2,…,ym]。然后使用 Y Y Y计算标量损失 l l l。假设向量 v v v恰好是标量损失 l l l关于向量 Y Y Y的梯度,则向量 v v v称为 grad_tensor (梯度张量)。
对于一个向量输入 v ⃗ \vec{v} v,backward方法计算的是 J T ⋅ v ⃗ J^{T} \cdot \vec{v} JT⋅v。参数 grad_tensor 就是这里的 v ⃗ \vec{v} v,需要与 Tensor 本身有相同的size。如果 v ⃗ \vec{v} v恰好是标量函数的梯度 l = g ( y ⃗ ) l=g(\vec{y}) l=g(y),即
v ⃗ = l = g ( y ⃗ ) = ( ∂ l ∂ y 1 ⋯ ∂ l ∂ y m ) T \vec{v}=l=g(\vec{y})=\left(\begin{array}{lll} \frac{\partial l}{\partial y_{1}} & \cdots & \frac{\partial l}{\partial y_{m}} \end{array}\right)^{T} v=l=g(y)=(∂y1∂l⋯∂ym∂l)T
损失函数 l = g ( y ⃗ ) l=g(\vec{y}) l=g(y)是一个从向量 y ⃗ \vec{y} y到标量 l l l的映射,那么 l l l对于 y \mathrm{y} y的梯度是 ( ∂ l ∂ y 1 ⋯ ∂ l ∂ y m ) \left(\frac{\partial l}{\partial y_{1}} \cdots \frac{\partial l}{\partial y_{m}}\right) (∂y1∂l⋯∂ym∂l)。
根据链式法则,损失函数 l l l相对于 x ⃗ \vec{x} x的梯度就是 y ⃗ = f ( x ⃗ ) \vec{y}=f(\vec{x}) y=f(x)和 l = g ( y ⃗ ) l=g(\vec{y}) l=g(y)的雅可比向量积:
J T ⋅ v ⃗ = ( ∂ y 1 ∂ x 1 ⋯ ∂ y m ∂ x 1 ⋮ ⋱ ⋮ ∂ y 1 ∂ x n ⋯ ∂ y m ∂ x n ) ( ∂ l ∂ y 1 ⋮ ∂ l ∂ y m ) = ( ∂ l ∂ x 1 ⋮ ∂ l ∂ x n ) J^{T} \cdot \vec{v}=\left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{1}} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_{1}}{\partial x_{n}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right)\left(\begin{array}{c} \frac{\partial l}{\partial y_{1}} \\ \vdots \\ \frac{\partial l}{\partial y_{m}} \end{array}\right)=\left(\begin{array}{c} \frac{\partial l}{\partial x_{1}} \\ \vdots \\ \frac{\partial l}{\partial x_{n}} \end{array}\right) JT⋅v= ∂x1∂y1⋮∂xn∂y1⋯⋱⋯∂x1∂ym⋮∂xn∂ym ∂y1∂l⋮∂ym∂l = ∂x1∂l⋮∂xn∂l
这种计算雅可比矩阵并将其与向量 v ⃗ \vec{v} v相乘的方法使PyTorch能够轻松地为非标量输出提供外部梯度。
3、计算图
Pytorch训练步骤为:
- 原始函数建立计算图,将问题转化成一种有向无环图。
- 进行正向传播,计算出中间节点,并记录计算图中的节点依赖关系。
- 反向传播,从输出开始遍历计算图,计算输出对于每个节点的导数。
可以看出来,计算图是这里的关键,是自动微分的工程基础。计算图就是用图的方式来表示计算过程,每一个数据都是计算图的一个节点,数据之间的计算即流向关系由节点之间的边来表示。它将多输入的复杂计算表达成了由多个基本二元计算组成的有向图,并保留了所有中间变量,这种结构天然适用于利用链式法则进行自动求导,可以完全向用户隐藏求导过程。
从概念上讲,Autograd 在由函数对象组成的有向无环图(DAG)中记录数据(张量)和所有已执行的操作(以及由此产生的新张量)。 在此 DAG 中,叶子是输入张量,根是输出张量。 通过从根到叶跟踪此图,可以使用链式规则自动计算梯度。
在正向传播中,Autograd 同时执行两项操作:
运行请求的操作以计算结果张量,并且在 DAG 中维护操作的梯度函数。
当在 DAG 根目录上调用.backward()时,反向传递开始。 autograd然后:
从每个.grad_fn计算梯度, 将它们累积在各自的张量的.grad属性中,然后 使用链式规则,一直传播到叶子张量。
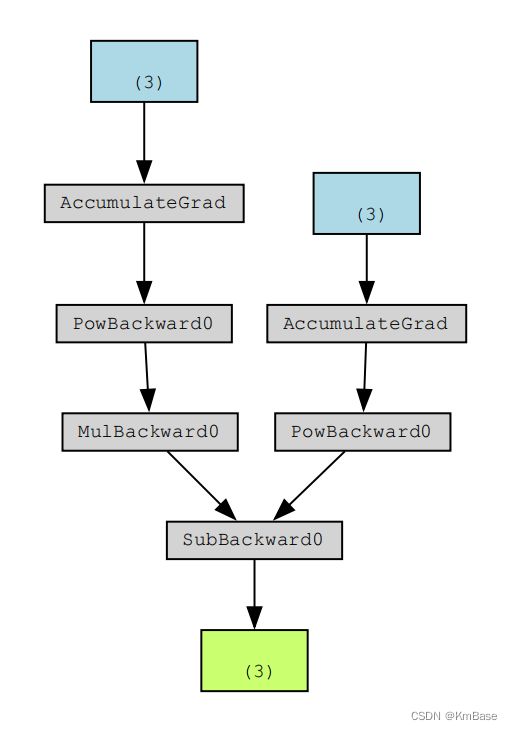
下面是DAG 的直观表示。 在图中,箭头指向前进的方向。 节点代表正向传播中每个操作的反向函数。 蓝色的叶节点代表叶张量a和b。
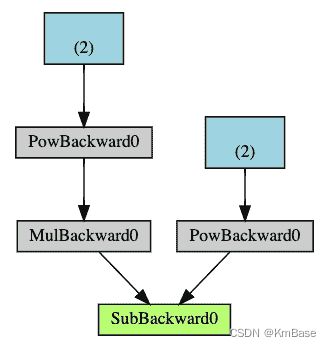
三、实例
import torch
from torchviz import make_dot
a = torch.tensor([2., 3.,4], requires_grad=True)
b = torch.tensor([6., 4.,5.], requires_grad=True)
print(a)
Q = 3*a**3 - b**2
external_grad = torch.tensor([1., 1.,1.])
Q.backward(gradient=external_grad)
# check if collected gradients are correct
print(9*a**2 == a.grad)
print(-2*b == b.grad)
print(Q)
g = make_dot(Q)
g.view()
参考文献
深度学习利器之自动微分(2)