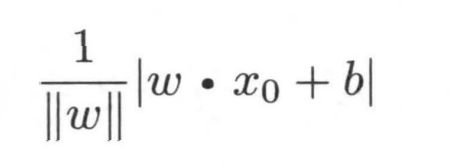【机器学习】感知机模型 python感知机实现代码
感知机模型
感知机模型的对偶形式
感知机是一种判别模型,使用于二分类问题,输入为实例的特征向量,输出实例的类别;取-1和+1分被称为负类和正类。。感知机学习主要是求出将训练数据能够进行线性划分的分离超平面,所以就有了基于误分类的损失函数,利用梯度下降法对损失函 数进行极小化,求得感知机模型 感知机学习算法具有简单而易于实现的优点,分为 原始形式和对偶形式 。
首先我们来看看感知机模型
模型:由输入空间到输出空间的如下函数:
f ( x ) = s i g n ( w • x + b ) f(x) = sign (w•x + b) f(x)=sign(w•x+b)
sign()为符号函数 ;
w,b:为模型参数(w : 权值或权值向量,b:偏置常量,w•x :内积(向量相乘再求和 )
)
为得到 S ,即确定模型参数w,b,定义损失函数并极小化
损失函数:在感知机模型中损失函数的一个自然选择是误分类点的总数。但是,这样的损失函数不是参数w,b的连续可导函数,不易优化。损失函数的另一个选择是误分类点到超平面的总距离,感知机所采用的就是这个损失函数。为此,首先写出输入空间 中任一点 Xo 到超平面距离:
||w|| 是 w的L2范数
对于误分类数据(xi,yi):
− y i ( w • x i + b ) > 0 -yi(w•xi + b) > 0 −yi(w•xi+b)>0
误分类点xi到S的距离:
- 1 / ||w|| * yi*(w•xi + b)
误分类点特征:
w • x i + b > 0 , y i = − 1 w•xi + b >0, yi = -1 w•xi+b>0,yi=−1
w • x i + b < 0 , y i = + 1 w•xi + b <0,yi = +1 w•xi+b<0,yi=+1
设S的误分类点集合为M,则误分类点到S的总距离:
− 1 / ∣ ∣ w ∣ ∣ ∑ y i ( w • x i + b ) ( x i ∊ M ) -1/||w|| ∑ yi (w•xi + b) (xi ∊ M) −1/∣∣w∣∣∑yi(w•xi+b)(xi∊M)
判断误分类点
真 实 值 ∗ 预 测 值 = + 1 正 确 分 类 ; 真实值 * 预测值 = +1 正确分类; 真实值∗预测值=+1正确分类;
真 实 值 ∗ 预 测 值 = − 1 误 分 类 ; 真实值 * 预测值 = -1 误分类; 真实值∗预测值=−1误分类;
不考虑 1 / ||w|| --> 损失函数 :
L ( w , b ) = − ∑ y i ( w • x i + b ) ( x i ∊ M ) L(w,b) = -∑ yi (w•xi + b) (xi ∊ M) L(w,b)=−∑yi(w•xi+b)(xi∊M)
- 选取损失函数最小的模型参数w,b
感知机学习算法:随机梯度下降法,任选一个超平面w0,b0,然后梯度下降法不断地极小化目标函数。极小化过程不是一次使M中所有误分类点的梯度下降,而是一次随机选取一个误分类点使其梯度下降;
损失函数L(w,b)的梯度由:
∇ w L ( w , b ) = − ∑ y i x i ( x i ∊ M ) ∇w L(w,b) = -∑yixi (xi ∊ M) ∇wL(w,b)=−∑yixi(xi∊M)
∇ b L ( w , b ) = − ∑ y i ( y i ∊ M ) ∇b L(w,b) = -∑yi (yi ∊ M) ∇bL(w,b)=−∑yi(yi∊M)
随机选取误分类点(xi,yi),对w,b进行更新
w ⬅ w+ɧyixi
b ⬅ b+ɧyi
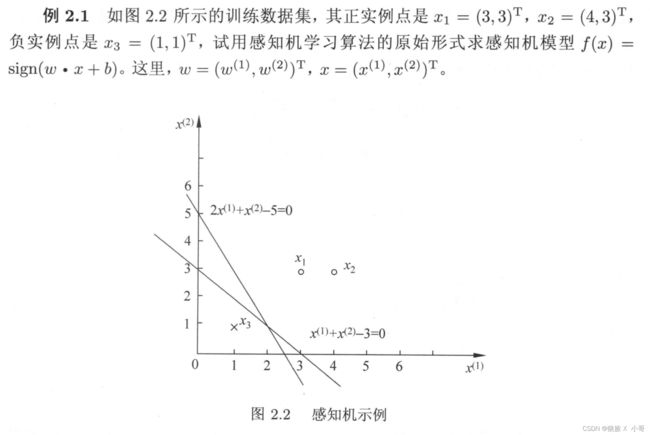
解:构建最优化问题
m i n L ( w , b ) = − ∑ y i ( w • x i + b ) ( x i ∊ M ) min L(w,b) = -∑yi(w•xi + b) (xi ∊ M) minL(w,b)=−∑yi(w•xi+b)(xi∊M)
代码示例:
import numpy as np
import matplotlib.pyplot as plt
p_x = np.array([[3, 3], [4, 3], [1, 1]]) # 创建数据集 x值
y = np.array([1, 1, -1]) # 标记数据集 1:正类;-1:负类 y值
plt.figure() # 创建图像
for i in range(len(p_x)): # 遍历数据集 在图中标记数据集各点
if y[i] == 1:
plt.plot(p_x[i][0], p_x[i][1], 'ro') # 将数据集中正类点标记为红色实心点
else:
plt.plot(p_x[i][0], p_x[i][1], 'bo') # 负类标记为蓝色实心点
w = np.array([1, 0]) # 初始化权重系数w
b = 0 # 初始化偏移常数b
delta = 1 # 步长 1
for i in range(100):
choice = -1 # 初始化标记参数choice
for j in range(len(p_x)):
if y[j] != np.sign(np.dot(w, p_x[0]) + b): # w与p_x内积 + b > 0 则sign=1;< 0 则sign=-1 (sign == y[i] 正确分类)
choice = j
break
if choice == -1:
break
w = w + delta * y[choice] * p_x[choice] # 更新参数
b = b + delta * y[choice]
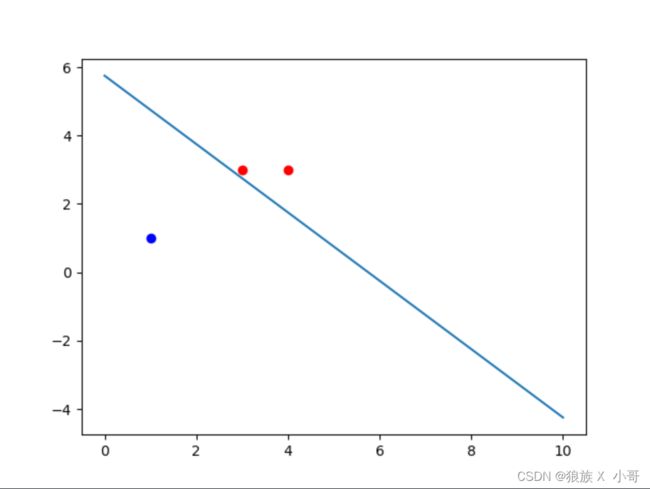
line_x = [0, 10] # 绘制x坐标系
line_y = [0, 0]
for i in range(len(line_x)):
line_y[i] = (-w[0] * line_x[i] - b) / w[1] # 绘制超平面
plt.plot(line_x, line_y)
plt.savefig("picture.png")
感知机模型的对偶形式