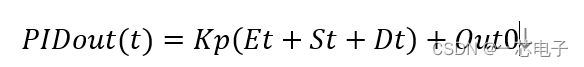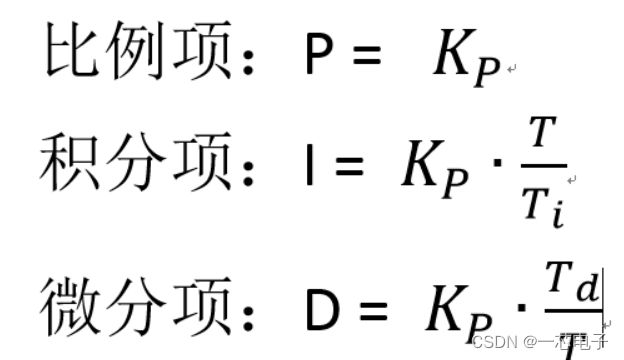PID算法详解

---

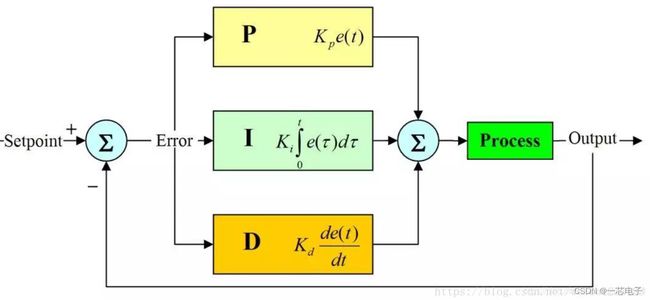
什么是pid

PID算法是一种具有预见性的控制算法，其核心思想是：
1>. PID算法不但考虑控制对象的当前状态值（现在状态），而且还考虑控制对象过去一段时间的状态值（历史状态）和最近一段时间的状态值变化（预期）,由这3方面共同决定当前的输出控制信号；
2>.PID控制算法的运算结果是一个数，利用这个数来控制被控对象在多种工作状态（比如加热器的多种功率，阀门的多种开度等）工作，一般输出形式为PWM，基本上满足了按需输出控制信号，根据情况随时改变输出的目的。

比例（p）控制

比例控制是一种最简单的控制方式。其控制器的输出与输入误差信号成比例关系。当仅有比例控制时系统输出存在稳态误差（Steady-state error）。
设某控制系统：用户设定值为SV(也就是希望通过PID控制算法使被控制对象的状态值保持在SV的附件)。

1>从系统投入运行开始，控制算法每隔一段时间对被控制对象的状态值进行采样。由此，可得到开机以来由各个采样时间点被控制对象的状态值所形成的数据序列：
X1,X2, X3, X4, … Xk-2,Xk-1,Xk
说明：
X1：开机以来的第一次采样值
Xk: 目前的采样值（最近一次的采样值）
2>从这个采样值序列中提取出三方面信息：
①当前采样值Xk与用户设定值SV之间的差值：Ek
Ek =Sk-Xk
分析Ek:
Ek>0：说明当前状态值未达标
Ek=0：说明当前控制状态值正好满足要求
Ek<0：说明当前状态值已经超标
结论：Ek反应了控制对象当前值与设定值的偏差程度，可以根据Ek的大小对输出信号OUT进行调整：偏差程度大OUT增大，偏差程度小OUT减小。即输出信号的强弱与当前偏差程度的大小成比例，所以根据Ek的大小来给出控制信号OUT的当前值的算法称为比例控制（Proportion）。用数学模型可以表示为：
POUT=（Kp*Ek）+Out0
Kp:一般称之为比例系数，可以理解为硬件上的放大器（或衰减器），适当选取Kp将当前误差值Ek
按一定的增益放大或缩小，以提高控制算法的相应速度。
Out0:是一个常数，目的是为了当Ek为0时，确保输出信号不为0，以不至于在当前值与设定值相等时控制器输出信号OUT为0，系统处于无控制信号的失控状态。

积分（I）控制

PID控制器中的积分对应于图1中误差曲线 与坐标轴包围的面积（图中的灰色部分）。PID控制程序是周期性执行的，执行的周期称为采样周期。计算机的程序用图1中各矩形面积之和来近似精确的积分，图中的TS就是采样周期。

积分运算示意图
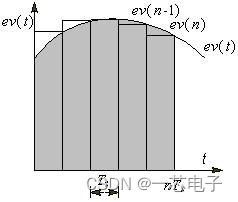
每次PID运算时，在原来的积分值的基础上，增加一个与当前的误差值ev（n）成正比的微小部分。误差为负值时，积分的增量为负。
手动调节温度时，积分控制相当于根据当时的误差值，周期性地微调电位器的角度，每次调节的角度增量值与当时的误差值成正比。温度低于设定值时误差为正，积分项增大，使加热电流逐渐增大，反之积分项减小。因此只要误差不为零，控制器的输出就会因为积分作用而不断变化。积分调节的“大方向”是正确的，积分项有减小误差的作用。一直要到系统处于稳定状态，这时误差恒为零，比例部分和微分部分均为零，积分部分才不再变化，并且刚好等于稳态时需要的控制器的输出值，对应于上述温度控制系统中电位器转角的位置L。因此积分部分的作用是消除稳态误差，提高控制精度，积分作用一般是必须的。
PID控制器输出中的积分部分与误差的积分成正比。因为积分时间TI在积分项的分母中，TI越小，积分项变化的速度越快，积分作用越强。
将投入运行以来的各个采样值都与设定值相减，可得到开机以来每个采样时刻的偏差序列数据：
E1，E2，E3 …Ek-2,Ek-1,Ek
说明：
E1：开机的第一个采样点与设定值的偏差
E1=SV-X1；
E2=SV-X2；
…
EK-2=SV-XK-2；
EK-1=SV-XK-1；
Ek: 当前的采样值与设定值的偏差
EK=SV-XK
分析开机以来的误差序列：
每个偏差值可能有：>0，<0，=0这三种可能的值，因为从开机到现在，控制算法不断输出控制信号对被控对象进行控制，导致了过去这段时间有时候超标（Ex<0）,有些时候未达标（Ex>0）,有时候正好满足要求（Ex=0）;如果将这些偏差值进行累加求代数和得到Sk,即：

Sk=E1+E2+E3+…+Ek-2+Ek-1+Ek
分析Sk:
Sk>0：过去大多数时候未达标
Sk=0：过去控制效果较理想
Sk<0：过去大多数时候已经超标

结论：1.通过对Sk的分析，可以对控制算法过去的控制效果进行综合评估。体现了控制算法按照原来的方式输出的控制信号导致了现在的控制结果，所以应该利用这个值来对当前要输出的控制信号OUT进行修正，以确保控制对象会在将来的一小段时间尽快达到用户设定的值。
2.Sk实际上是过去每个时间点的误差相加，与数学上的定积分运算类似，因此根据Sk对输出信号进行调节的算法称积分（integral）算法。所以积分控制的数学模型为：
IOUT = Kp*Sk+Out0
Kp是一常数，其目的类似硬件上的放大器，用于将Sk放大或衰减；
Out0是一常数，为了在历史积分偏差值为0时确保系统有一个输出值，避免失控；

微分（D）控制

误差的微分就是误差的变化速率，误差变化越快，其微分绝对值越大。误差增大时，其微分为正；误差减小时，其微分为负。控制器输出量的微分部分与误差的微分成正比，反映了被控量变化的趋势。
有经验的操作人员在温度上升过快，但是尚未达到设定值时，根据温度变化的趋势，预感到温度将会超过设定值，出现超调。于是调节电位器的转角，提前减小加热的电流。这相当于士兵射击远方的移动目标时，考虑到子弹运动的时间，需要一定的提前量一样。

阶跃响应曲线 图2中的c (∞)为被控量c (t)的稳态值或被控量的期望值，误差e(t) = c (∞) - c (t)。在图2中启动过程的上升阶段，当 时，被控量尚未超过其稳态值。但是因为误差e(t)不断减小，误差的微分和控制器输出的微分部分为负值，减小了控制器的输出量，相当于提前给出了制动作用，以阻碍被控量的上升，所以可以减少超调量。因此微分控制具有超前和预测的特性，在超调尚未出现之前，就能提前给出控制作用。 闭环控制系统的振荡甚至不稳定的根本原因在于有较大的滞后因素。因为微分项能预测误差变化的趋势，这种“超前”的作用可以抵消滞后因素的影响。适当的微分控制作用可以使超调量减小，增加系统的稳定性。 对于有较大的滞后特性的被控对象，如果PI控制的效果不理想，可以考虑增加微分控制，以改善系统在调节过程中的动态特性。如果将微分时间设置为0，微分部分将不起作用。 微分时间与微分作用的强弱成正比，微分时间越大，微分作用越强。如果微分时间太大，在误差快速变化时，响应曲线上可能会出现“毛刺”。 微分控制的缺点是对干扰噪声敏感，使系统抑制干扰的能力降低。为此可在微分部分增加惯性滤波环节。 最近两次的偏差之差

Dk=Ek-Ek-1
说明：
Ek：当前的偏差
Ek-1: 基于当前的前一个采样时刻的偏差值（即上一次的偏差值）；
分析Dk:
Dk>0：说明从上一采样时刻到当前误差有增大趋势
Dk=0：说明从上一采样时刻到当前误差平稳
Dk<0：说明从上一采样时刻到当前误差有减小趋势
Dk>0 Dk=0 Dk<0

结论：

1. Dk能够说明从上次采样到当前采样的这段时间被控制对象的状态变化趋势，这种变化的趋势很可能会在一定程度上延续到下一个采样时间点，所以可以根据这个变化趋势（Dk的值）对输出信号OUT进行调整，达到提前控制的目的。
2. Dk形如数学上的微分运算，反应了控制对象在一段时间内的变化趋势及变化量，所以利用Dk对控制器输出信号进行调节的算法称为微分（differential）算法。可以用数学模型表达为

IOUT = Kp*Dk+Out0
Kp：为一常数，可理解为硬件上的放大器或衰减器，用于对输出信号OUT的增益进行调整；
Out0:为一常数，为了在Dk为0时确保OUT都有一个稳定的控制值，避免失控。

PIDOUT = POUT + IOUT + DOUT0

PIDOUT = Kp（Ek+Sk+Dk）+OUT0

注：上面是基本思想

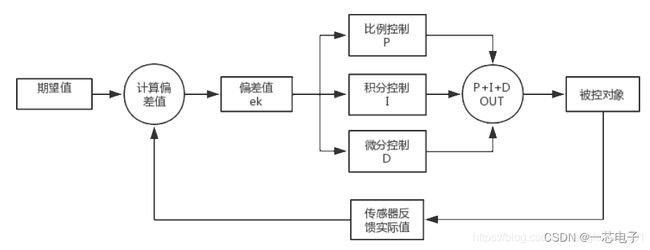
PID使用

上图的通俗表示：

二、模拟PID控制原理

这里的 Et、St、Dt是上面的Ek、Sk、Dk

这个是连续的公式，转换成离散的模型是：

实际使用的也是离散化的模型
由于模拟的微积分运算对应计算机来说是不太好写代码的，所以要利用采样将数据离散化

PIDout(t) -------------输出曲线，pid输出值随时间的变化曲线

Kp --------------比例系数

E(t)------------- 偏差曲线，设定值与实际值的偏差随时间的变化曲线

Ti--------------- 积分时间

Td--------------微分时间

T--------------计算周期

整合一下为：

其中：

这个就是实际使用需要调整的参数

增量式PID

C语言实现pid算法

/**************************************************************************
函数功能：位置式PID控制器
入口参数：编码器测量位置信息，目标位置
返回  值：电机PWM
根据位置式离散PID公式 
pwm=Kp*e(k)+Ki*∑e(k)+Kd[e（k）-e(k-1)]
e(k)代表本次偏差 
e(k-1)代表上一次的偏差  
∑e(k)代表e(k)以及之前的偏差的累积和;其中k为1,2,,k;
pwm代表输出
**************************************************************************/
int Position_PID (int position,int target)
{ 	
	 static float Bias,Pwm,Integral_bias,Last_Bias;
	 Bias=target-position;                                  //计算偏差
	 Integral_bias+=Bias;	                                 //求出偏差的积分
	if(Integral_bias>3000)Integral_bias=3000;
	if(Integral_bias<-3000)Integral_bias=-3000;
	 Pwm=Position_KP*Bias+Position_KI*Integral_bias+Position_KD*(Bias-Last_Bias);       //位置式PID控制器
	 Last_Bias=Bias;                                       //保存上一次偏差 
	 return Pwm;                                           //增量输出
}

/**************************************************************************
函数功能：增量PI控制器
入口参数：编码器测量值，目标速度
返回  值：电机PWM
根据增量式离散PID公式 
pwm+=Kp[e（k）-e(k-1)]+Ki*e(k)+Kd[e(k)-2e(k-1)+e(k-2)]
e(k)代表本次偏差 
e(k-1)代表上一次的偏差  以此类推 
pwm代表增量输出
****************************************************************************/

struct {
    float set_speed;//设定速度 
    float actual_speed;//实际速度
    float error;//偏差  
    float error_next;//上一个偏差  
    float error_last;//上上一个偏差 
    float kp,ki,kd;//定义比例，积分，微分参数  
     
}pid;
void pid_init()
{
    pid.set_speed = 0.0;
    pid.actual_speed = 0.0;
    pid.error = 0.0;
    pid.error_next = 0.0;
    pid.error_last = 0.0;
    //可调节PID 参数。使跟踪曲线慢慢接近阶跃函数200.0 // 
    pid.kp = 0.2;
    pid.ki = 0.01;
    pid.kd = 0.2;
}


float pid_realise(float speed)//实现pid  
{
    pid.set_speed = speed;//设置目标速度  
    pid.error = pid.set_speed - pid.actual_speed;
    float increment_speed;//增量
     
    increment_speed = pid.kp*(pid.error-pid.error_next)+pid.ki*pid.error+\
    pid.kd*(pid.error-2*pid.error_next+pid.error_last);//增量计算公式  
    
    pid.actual_speed+= increment_speed;
    pid.error_last = pid.error_next;//下一次迭代  
    pid.error_next = pid.error;
    return pid.actual_speed; 
    
}

下一篇文章实现平衡小车的直立环、速度环、转向环