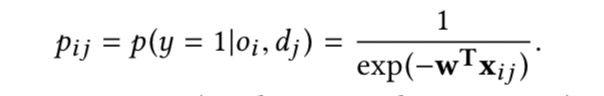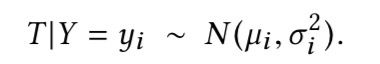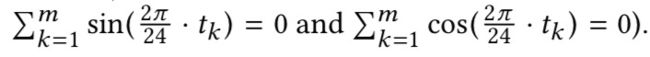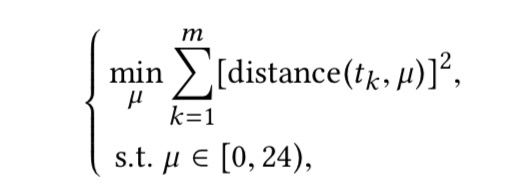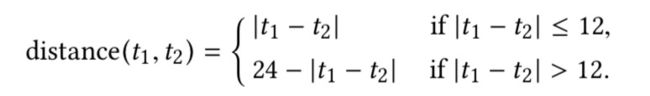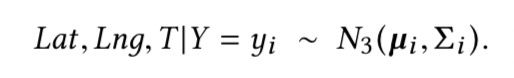基于组合优化的出租车订单调度模型

出租车预订应用程序在世界各地非常流行，因为它们为用户提供了快速响应时间等便利。出租车预订应用程序的关键组件是调度系统，该系统旨在提供司机和乘客之间的最佳匹配。传统的调度系统按顺序向乘客调度出租车，目的是使每个订单的驾驶员接受率最大化。然而，传统的系统可能导致较低的全球成功率，这会降低骑手使用应用程序时的体验。在本文中，我们提出一个新的系统，试图优化调度出租车服务多个预订。该系统旨在最大化全球成功率，从而优化整体旅行效率，从而提高用户体验。为了进一步提高用户体验，我们还提出了一种在出租车预订应用程序启动后预测用户目的地的方法。该方法利用贝叶斯框架对用户的目的地分布进行建模。

我们使用严格的A/B测试，将我们的新出租车调度方法与使用北京收集的数据的最新模型进行比较。实验结果表明，该方法的全局成功率（从80%提高到84%）明显优于其他现有模型。此外，我们在其他指标如用户等待时间和取货距离上也取得了显著的改进。对于我们的目的地预测算法，我们将前3位的预测精度从89%提高到93%，表明我们的模型优于基线模型。提出的出租车调度和目的地预测算法都部署在我们的在线系统中，每天为数千万用户提供服务。

GPS和4G网络的最新进展使得移动出租车应用越来越受欢迎。这些应用程序每天收集大量的个人轨迹。收集到的数据为我们提供了一个前所未有的自动发现用户行为知识的机会，可用于构建不同应用领域的实时智能决策系统，如乘客查询[7、12、13、24]、出租车需求预测[16、17]、路线规划[14、22]和出租车订单调度[8、11]。

订单调度的质量直接影响到乘客的使用体验和出租车的运营效率。因此，如何有效地调度订单是一个中心任务。以前的一些订单调度工作[3，10]集中在如何为每个订单找到最近的司机或最短的行程时间司机。当订单到达时，这样的系统会选择最近的一个驱动程序，而不会判断这些驱动程序是否更适合其他订单。因此，这些方法不能保证所有订单的全局最短行程时间。[19]中的作者提出了一个新的模型，它基于一个称为NTuCab的多代理体系结构。该模型以每个agent为计算单元，以全局最小的等待时间和取货距离为目标。每个计算单元处理N个顺序/驱动程序对，并且每个顺序仅分派给一个驱动程序。如果匹配的驱动程序不接受订单，订单将被发送到另一个驱动程序。

上述方法的一个缺点是调度时间长

时间和低成功率，因为方法没有优化

1个

总成功率。在滴滴楚星，数百万的职业车手-

每天为1000多万旅客提供交通服务。高峰时段，滴滴楚星需要每秒为十几万名乘客配车。因此，这些订单的总成功率成为评价底层订单调度系统性能的主要指标。

针对滴滴楚星的订单调度问题，提出了一种新的组合优化模型。在这个模型中，我们将一个订单分配给多个驱动程序，目的是最大化这些订单的总成功率。当多个驱动程序接收到相同的命令时，第一个接受的驱动程序获取该命令。如果订单未被接受，则进入下一轮发货，直到订单被接受或取消。

调度系统中的一个订单通常有三个重要的元素——出发时间、订单的出发地和目的地。一般情况下，我们只需选择当前时间和乘车地点作为订单的出发时间和出发地点，这非常适合大多数出租车呼叫情况。然而，不同的人往往去非常不同的目的地。即使是同一个人，在不同的出发时间和地点，目的地也可能不同。但是，它为用户输入目的地的全名带来了额外的工作。因此，如果在用户打开应用程序时能够准确地预测预期的目的地，则用户体验可以大大增强。目前的方法大多是利用所有用户的轨迹数据来训练一个模型，然后利用当前行程的信息，结合一些辅助信息，如时间、交通状况等来预测预定目的地[9、21、23]。

文[20]中给出了一种典型的方法，提出了一种基于多层感知的神经网络，该神经网络采用用户初始轨迹数据等输入数据和驾驶员身份证、用户信息、出行出发时间等其他元数据，训练后可以预测大部分行程。但是，该模型不太依赖于可以从数据中导出的特定于问题的信息。它在很大程度上依赖于行程的初始连续轨迹数据。一旦这部分数据被丢弃，预测精度就会大大降低。这一点在论文的实验中也得到了证明。[4]中的工作使用了驾驶员自己的历史行程数据来训练HMM模型。该模型将一天中的时间划分为几个主观的部分，如上午、中午和晚上，这种处理破坏了时间的连续性。

以前的方法不适用于滴滴楚星的目的地预告问题，因为乘客一打开应用程序就需要进行预测，但无法立即获得当前行程的轨迹数据。此外，与以往大多数试图最小化预测目的地和实际目的地之间的距离的方法不同，我们的目标是确定用户想要去的确切目的地。事实上，即使预测的目的地是真实目的地的别名，乘客也很可能将其视为一个不熟悉的位置，而只是手动输入地址。因此，我们的系统将每个用户的历史旅游目的地集合作为目的地预测的候选集合。个人历史旅行统计在不同的人之间有很大的不同。以2015年为例，至少使用过滴滴楚星一次的用户，每人每年的出租车预订使用量约为20辆。然而，由于高频用户每天打开应用程序，而低频用户在一年内打开应用程序的次数不到10次，因此分布不均。从如此稀少的数据中获得准确的个人统计数据是一项重大挑战。

通过分析大量乘客的出租车预订行为，我们得到了一些有趣的观察结果。在此基础上，我们提出了一个三元高斯分布下，考虑出发经度、纬度和出发时间的贝叶斯目的地预测模型。该模型利用个人历史旅行数据进行训练。训练后的模型可以根据出发经度、纬度和出发时间计算出用户历史目的地的概率。然后，它提供一个按概率排列的预测目的地列表。

本文的其余内容如下：第二节介绍了出租车调度系统，第三节介绍了目的地预测系统，第四节通过实验验证了两种模型的有效性，第五节对本文进行了总结。

 

2 订单调度系统

我们首先介绍一些符号。我们的订单调度系统的目标是使成功率最大化，用ES R表示。

如果有N个订单要发送给M个驱动程序，我们将发送结果表示为一个矩阵

在滴滴楚星的业务场景中，一个订单被发送给多个司机，每个司机根据自己的喜好决定是否接受。对于每一个订单，它是否被一个司机接受，直接关系到每个司机的接受概率。因此，订单调度的关键问题是估计每个驾驶员接受订单的概率。如果我们可以估计矩阵的元素表示每个驱动程序接受每个订单的概率，那么我们可以估计一个订单被其中一个驱动程序接受的概率。因此，我们将订单调度模型分为两个子模型。一个模型预测每个司机的行为，在这个模型中，我们估计司机接受订单的概率。另一个模型利用估计的可接受概率来建立目标ESR最大化的优化问题，然后解决潜在的优化问题。

2.1驾驶员行为预测模型

由于驱动程序的操作有两个值：accept或reject（not accept），我们使用一个0-1值的二进制变量y来表示操作结果，其中1代表accept，0代表reject。我们假设驾驶员的行为服从一个独立且相同的概率分布。

我们使用pij来表示司机dj接受订单oi的概率。概率取决于许多因素，例如订单的货币价值、行驶距离和方向等。这样的信息可以被编码成特征向量席j，它与订单OI、驾驶员DJ以及它们之间的相互作用有关。鉴于席J，我们想估计接受概率如下：

pij=p（y=1 | xij）。

将驾驶员行为预测问题作为一个典型的二元分类问题，利用历史驾驶员顺序对（oi，dj）产生的特征及相关结果对分类器进行训练。

 

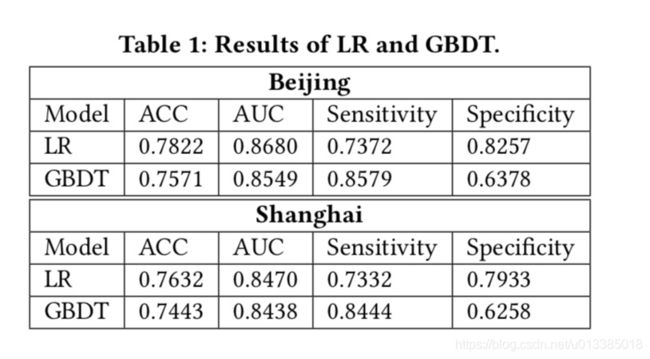
在这项工作中，我们尝试了两种流行的模型：线性logistic回归模型-

sion（LR）[5]和梯度增强决策树（GBDT）[6，15]。我们为不同的城市训练不同的模型并评估这两种方法准确度（ACC）和ROC曲线下面积）。北京和上海的实验结果显示在表1。

我们注意到，LR和GBDT都被广泛使用。我们的经验-实验表明，对于我们的数据，LR稍微更准确一些。因此，我们选择LR作为系统的预测模型，其中概率pi j可以写成

我们的系统使用SGD（随机梯度下降）来训练模型参数[2，25]。预测模型考虑了各种因素. 这些因素可以总结如下：

•订单司机相关特征：取车距离、该订单被多少个司机看到，订单是否在司机当前行驶方向的前方还是后方。

•订单相关特征：始发地和目的地之间的距离和预计到达时间（ETA）、目的地类别（机场、医院、学校、商业区等）、路线交通状况、目的地历史订单频率。

•驾驶员相关特征：长期行为（包括驾驶员的历史接受率、驾驶员的活动位置、驾驶员对不同广播距离的偏好等）和驾驶员的短期兴趣，如最近是否接受订单等。

•补充特征，如一周中的某天、一天中的某小时、附近的司机数量和附近的订单数量。

2. 组合优化模型

在我们的系统中，一个订单可以发送给多个司机，因此所有司机都有助于订单接受的概率。假设有N个订单要发送给M drivers，那么接受订单oi的概率为：

 

这是一个约束组合优化问题[18]。接下来我们将展示如何解决这个问题。

许多组合优化问题都是NP难问题，在多项式时间内没有有效的通用算法来求解这类问题。一种典型的方法是使用启发式算法来寻找近似解。常用的方法有爬山法、遗传算法、模拟退火算法等，通过平衡精度和性能，选择爬山法来解决问题。下面的算法1描述了详细的过程。

3. 目的地预测

3. 目的地预测

本节介绍我们提出的目的地预测系统。通过对滴滴楚星大量用户出租车预订情况的分析

行为方面，我们发现了一些有趣的模式：（1）同一个用户在相似的时间趋向于同一个目的地。具体来说，出发时间（一天中的时间）是预测用户预定目的地的最重要因素，其次是出发纬度和经度。有趣的是，日期变量（workday或holiday）可以将数据分成两组，具有不同的特征：workday目的地集中在家庭和工作场所；holiday目的地集中在购物中心和娱乐场所，等（2）同一用户即使在周末也倾向于去固定的地点购物，除了偶尔的紧急情况，如医生预约、商务旅行等。（3）订单的地点为目的地预测提供了有用的信息。其他信息如驾驶员信息、交通状况、行驶速度等与目的地的相关性较弱。

在此基础上，我们提出利用用户的历史数据，如出发时间、出发纬度和经度，利用贝叶斯规则对用户目的地的概率分布进行建模。

3.1模型说明

我们首先介绍表2中的一些符号。

我们观察到D只有两类，可以用来将用户的历史数据分为两个行为迥异的聚类，利用特征D对数据进行聚类预处理，并将历史数据中每个订单的日期作为时间性因素来衡量训练数据的重要性（由于篇幅有限，此处省略了细节）。我们提出的方法的目的是模拟用户目的地的概率分布。为了达到这个目的，我们使用贝叶斯公式来表示目的地{y1，y2，…，yi，…，yn}的条件概率，如下所示：

剩下的问题是在给定目的地的情况下，估计出发时间和地点（经纬度）的联合分布，即：p（T，Lng，Lat | Y=yi）。我们首先研究了出发时间T的条件概率分布p（T | Y=yi），给出了目的地yi。然后，我们将包括经度和纬度，以获得给定目的地yi的(T,Lng,Lat)）的联合条件概率分布。

3.2给定目的地出发时间的条件分布

图1显示了示例用户的出发时间对应目的地三里屯的直方图。直方图的形状与高斯分布非常相似。通过研究许多其他用户的案例，我们有类似的观察结果。因此，我们使用高斯分布来估计出发时间T的条件概率：

我们注意到变量T从0小时到23小时取循环值，然后重复。因此，平均μi和方差σi2不能用传统方法估计。例如，如果时间是8:00、9:00、10:00，则平均值是9:00，可以计算为（8+9+10）/3；但是如果时间是3:00、15:00、21:00，则平均值是21:00，而不是（3+15+21）/3=13。接下来我们将展示如何估计平均μi和方差σi2。

注意，时间变量是一个循环量。计算圆形量平均值的一种常用方法是将所有圆形变量转换为单位向量，计算向量的平均值，然后将结果转换回原始的圆形表示。给定时间t1，t2，…，tm，平均μ可以表示为：

这种方法简单直观，但在某些情况下，得到的结果偏离了真实值（例如，三次00:00:00、00:00:00、03:00:00的平均值是01:00:00，但向量的平均值是00:58:33）。此外，在某些情况下没有结果（例如

上述问题，我们提出了另一种计算离港时间平均值的方法，该方法也适用于任意圆形数值变量的平均值。

我们的方法基于以下观察。出发时间的平均值可以通过求解以下约束二次优化问题得到：

其中距离（t1，t2）表示两个圆形变量t1和t2的距离，定义如下：

3.3给定目的地出发时间、出发纬度和经度的联合条件分布

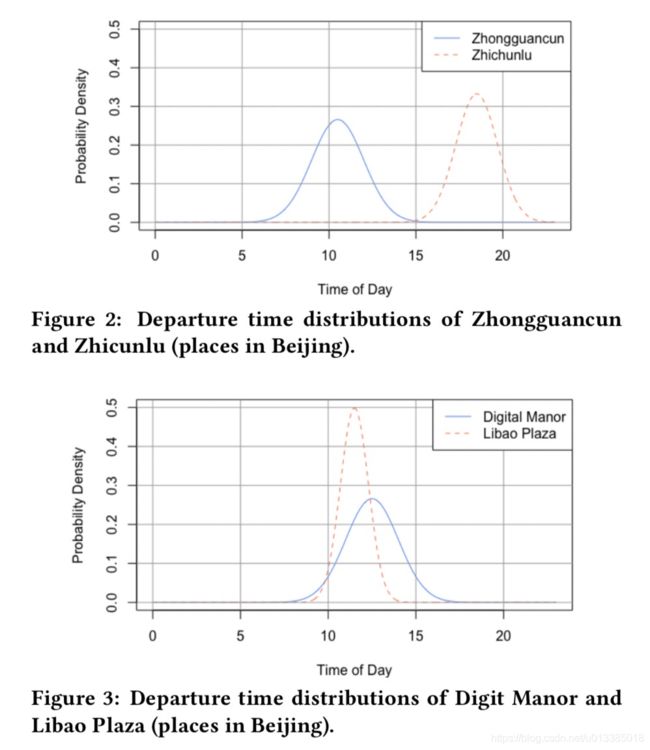
对于大多数用户来说，仅根据出发时间就可以获得对目的地的高精度预测。图2显示了乘客两个不同目的地出发时间的概率分布。我们发现，到中关村的旅客出发时间集中在11:00左右，到支村路的旅客出发时间集中在19:00左右。如果用户早上打开应用程序，那么去中关村的可能性就很大；晚上去支村路的可能性就很大。

对于其他一些用户来说，为了获得高精度的预测，需要综合其他信息。图3给出了一个典型的例子，表明数字庄园和丽宝广场的出发时间分布有相当多的重叠。因此，对于这个用户来说，仅仅基于出发时间是不可能给出目的地的准确预测的。

图4显示了该用户的两个不同目的地Digital Manor和Libao Square的分割时间、出发经度和纬度（T，Lng，Lat）的三维分布。我们可以看到，三维分布可以很容易地区分这两个不同的目的地。

为了找到合适的模型来描述这种三维联合分布，我们分析了出发时间和出发经度的联合分布散点图

 

每个用户的每个目的地的纬度（T，Lnü，Lat）。其分布符合三维高斯分布的形状。因此，我们可以假设给定用户和预定目的地，

 

为了验证这一假设，我们将经典统计学中的拟合优度检验的思想用于正态性检验。我们仍然使用用户自己的历史数据来估计分布参数（均值向量和协方差矩阵）。应该指出的是，Lat，Lnü，T都是圆形量，因此可以用前面描述的二次规划方法来估计平均向量和协方差矩阵。

3.4根据出发时间、出发纬度和经度预测目的地的完整步骤。

4实验

在这一部分中，我们将评估所提出的订单调度和目的地预测模型。对于订单调度模型，我们将我们的模型与其他两种使用多评价准则的方法进行了比较。对于目的地预测模型，目前还没有适合我们任务的方法。因此，我们将我们提出的方法与一个简单的基于KNN的方法进行比较，该方法在Didi Chux-ing的在线系统部署之前就已被使用。

4.1订单调度系统实验

基于以下考虑，我们进行了评估订单调度系统的实验。首先，为了设计评估指标，我们考虑了一般的出租车订单调度业务。然后，我们将我们的模型与业界广泛使用的其他两个模型进行比较[10，19]。我们将数据随机分成三个随机分区，并根据表3中的指标比较性能。此外，我们还研究了不同模型的详细行为，并提出了一些有趣的观察结果

4.1.1评估订单调度模型。订单调度系统影响许多核心指标，在这些指标中，我们选择了[1]中使用的一些关键业务指标，这些指标与我们在系统中使用的相似。我们把它们列在表3[1]中。

4.1.2实验方法。我们将我们提出的方法与业界广泛使用的两个模型进行了比较：一个是将每个订单分派给最适合订单的驱动程序[3，10]。另一种方法是将一批订单发送给司机，从而使整个等待时间最小化[19]。

模型1:[10]提出了一种实时交通环境下驾驶员最短驾驶时间的计算方法。[3] 提出了一种基于a*算法的订单调度方法

指标缩写。

服务呼叫百分比（成功率）SR

平均取车时间（从司机接受的命令到乘客上车的时间）APT

平均调度时间（从pas-ADT传感器发出命令到一个驾驶员接受命令的时间）ADT

已取消呼叫的百分比（取消率）CR

每个FU-cab的平均呼叫总数（车队利用率）FU

在这些研究的基础上，我们采用了一种基于学习排序的方法，利用历史数据得到一个公式来计算司机和订单的匹配分数。然后，我们向匹配得分最高的驾驶员发送一个订单（注意，在本文提出方法之前，滴滴楚星一直使用这种方法）。

模型2:[19]提出了一个基于多代理的订单调度系统，称为NTuCab。该系统在优化总体等待时间方面优于大多数其他系统。

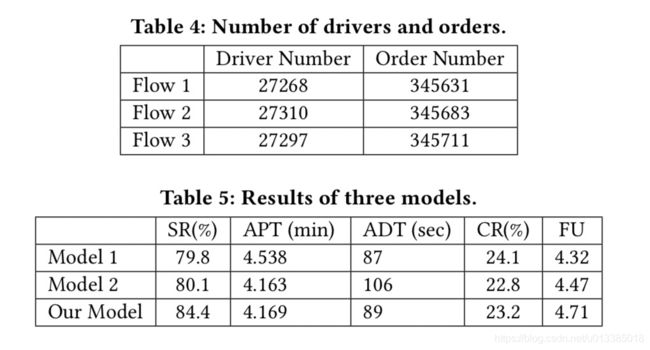
我们在北京（中国最大的城市）用一天的数据进行实验。数据包含100万个订单和8万个驱动程序。我们根据手机号码将数据平均分成三部分（流1、流2和流3）。驱动程序数量和订单数量汇总在表4中。我们分别在流程1、流程2和流程3中运行模型1、模型2和我们提出的模型。

4.1.3实验结果及分析。在系统在线运行一天后，我们在表5中报告了三个模型的以下评估指标。结果表明，在关键评价指标SR上，我们的模型明显优于其他两个模型。在平均提取时间（APT）指标上，我们的模型与模型2几乎相同，因为模型2试图优化APT，而在我们的模型中，APT是决定SR的一个重要因素。在平均调度时间（ADT）度量上，模型2甚至比模型1更差，因为在[19]中，模型2有一个关键约束：模型的每个调度单元只能处理相同数量的驱动程序和命令。这意味着许多订单或司机只能等待下一轮调度，导致调度时间更长。

图5描绘了三个模型的成功率与时间的关系。很明显，在晚上（23:00-次日凌晨5:00）订车相对较少的时候，三款车型的成功率都较高。这是因为有大量的免费车辆，预订相对较少，而且有足够的供应，使用何种订单调度模式并不重要。随着预订量的增加，特别是高峰时段（早上7点到9点，晚上17点到19点）和晚餐后的晚上（晚上21点到22点），由于汽车预订量大幅增加，加上实际可获得的免费车辆减少，成功率相对较低，导致供需不平衡。在这种情况下，我们的模型产生的成功率明显高于其他两个模型。

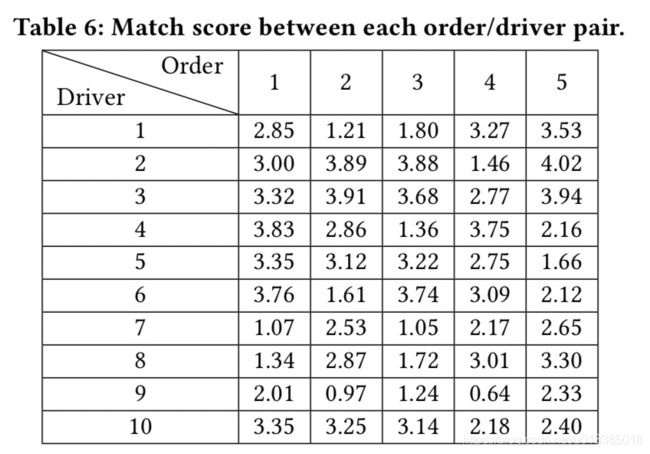
4.1.4案例研究。实验结果表明，该模型的成功率明显优于其他两种模型。为了说明三种模型的差异，我们构建了一个包含10个驱动和5个订单的综合数据集，并分析了这三个模型如何将5个订单分配给10个驱动。

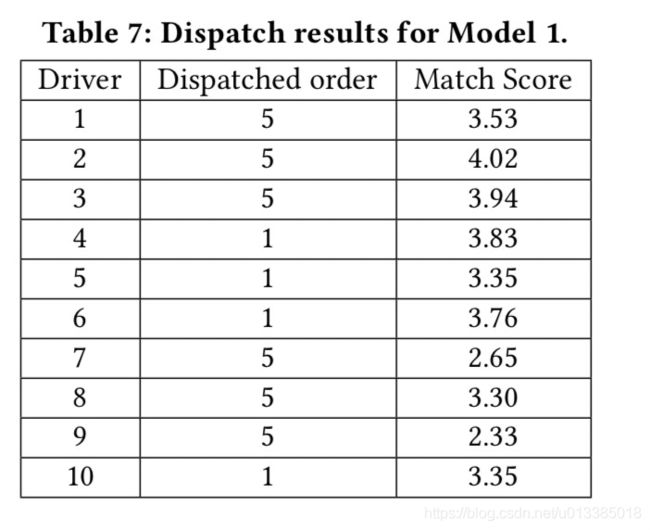
模型1首先计算每个驾驶员的所有候选订单的匹配分数，然后将得分最高的订单分配给驾驶员。从表6可以看出，order（5）对驾驶员的得分最高（1、2、3、7、8、9），order（1）对驾驶员的得分最高（4、5、6、10）。因此，根据为每个驱动器分配最高顺序的原则，将顺序（5）分配给驱动器（1、2、3、7、8、9），将顺序（1）分配给驱动器（4、5、6、10）。订单（2，3，4）只有在10个驱动程序对订单（1）和（5）做出选择（接受或拒绝）后才能发送，导致效率相对较低。这正是因为这种订单调度模型在不考虑全局的情况下，分别考虑了每个驱动程序和订单。模型1的调度结果如表所示

 

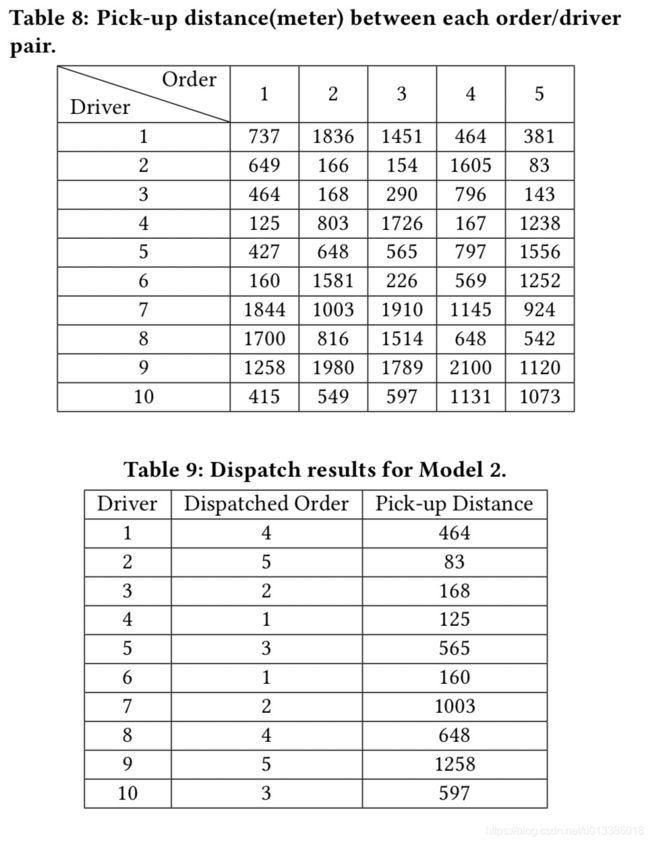
模型2的调度结果如表9所示，其目标是最小化总取车距离（见表8）。我们发现，与模型1不同，模型2将所有驱动程序和订单视为一个整体，因此每个订单可以分派给相同数量的驱动程序。由于该模型试图最小化总的提取距离，因此在所有三个模型中，模型输出的总提取距离最短。

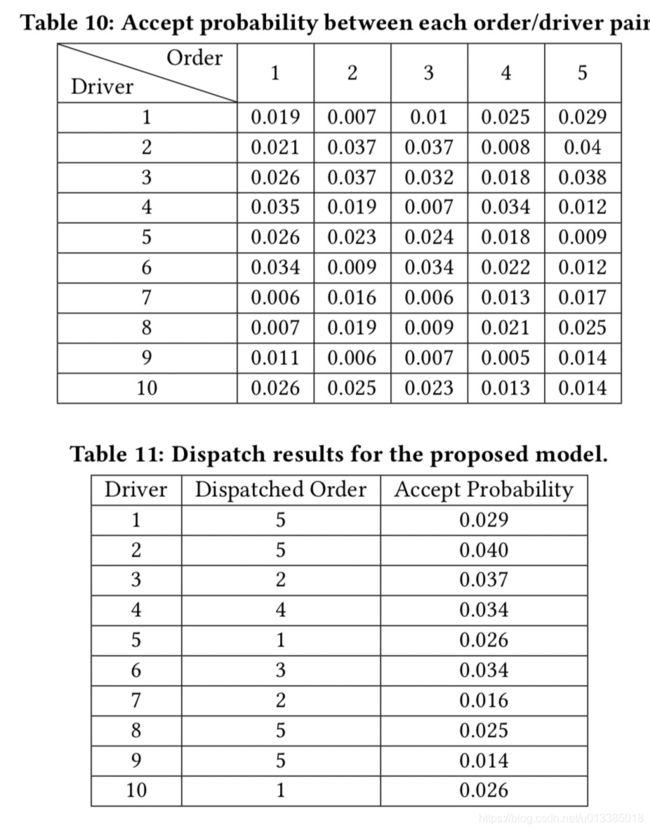
在所提出的模型中，我们首先通过公式（1）估计每个驾驶员接受每个订单的概率（详细结果见表10）。然后，根据接受概率矩阵，我们将订单发送给司机，使总成功率最大化，如下式（3）（详细结果见表11）。

接下来，我们分析了三个模型中每个订单的预期结果与总体成功概率之间的差异。我们使用等式（2）和表10中的接受概率来估计三个模型中每个订单的成功概率（结果如表12所示）。对于模型1，我们看到订单（1，5）具有更高的接受概率，并且订单（2，3，4）没有发送给任何驱动程序，导致概率为0。因此，成功的总概率很低，（0.116+0+0+0+0.138）/5=5.08%。模型2将订单和驱动因素作为一个整体考虑，并优化整个取件距离以获得调度结果。然而，最小化提货距离并不完全等同于最大化成功率，因为驾驶员接受订单不仅取决于提货距离，还取决于订单收入等其他因素。其总体成功概率为（0.068+0.052+0.046+0.045+0.053）/5=5.28%。模型以成功率为优化准则，调度结果的成功率最高（0.051+0.052+0.034+0.034+0.104）/5=5.5%。

 需要注意的是，上述成功概率与表5中的成功率有着显著的不同。表5中的成功率是滴滴楚星在线系统不同模型产生的实际结果，而上述的成功概率是在相同数据（仅包括5个订单和10个驱动程序）上不同模型的模拟结果，同时考虑到估计的驱动程序接受概率。

4.2目的地预测实验

如前所述，现有的目的地预测模型大多基于一些元数据和正在进行的行程数据。然而，在滴滴楚星，目的地预测发生在乘客创建订单之前。具体来说，预测系统是在滴滴楚星应用程序启动后立即调用的。届时，只能获得乘客的当前位置、当前时间、乘客身份等元数据。因此，现有方法[4、9、20、21、23]不适用于滴滴楚星的场景。

在我们的在线系统中部署目的地预测模型之前，滴滴点滴在线系统中使用了一个基线模型，该模型基于两个特征：出发时间和地点，采用K近邻法（K=100）。我们利用北京市3个月的出租车数据对两个模型进行了训练，并将我们提出的模型与基线模型在1、2和3个方面的精度进行了比较。测试数据集的实验结果（包括一周的数据）如图6所示。我们观察到我们提出的模型在很大程度上优于基线模型。

从图中可以看出，我们提出的目的地预测模型达到了93%左右的高精度，比基线模型的前3位精度高出4%。性能是合理的，因为对于任何用户来说，都会有一些不可预测的事件，例如看医生、旅行等，而且，还有许多新用户，而且对于他们来说，历史目的地统计数据不够高。

 进一步分析了不同工作日的预测结果，发现：（1）周末（周六、周日）的预测性能低于工作日（周一至周五）。这是因为在工作日，用户的出行模式比较规律，主要是在工作和家庭之间；在周末，出行模式会不规则，比如购物、娱乐等。（2）在工作日，周三的准确率最高，而周一和周五的准确率相对较低。从数据中，我们发现对于许多用户来说，私人活动和其他不规则的旅行发生在周五晚上和周一早上。（3） 在周末，相对于周日，周六的行程更不确定。我们的统计数据显示，许多个人旅行，如探亲访友，都发生在星期六上午。回程旅行通常在星期天下午。对于这些用户来说，周六的旅游目的地相对来说是随机的（朋友和亲戚、中转站等），周日的目的地相对来说是集中的（家）。

5结论与未来工作

本文提出了一种新的订单调度模型，并将其应用于滴滴楚星在线系统中。提出的模型旨在最大化全球成功率，从而优化整体交通效率，并提供最佳用户体验。我们将订单调度模型描述为一个组合优化问题，其中一个关键因素是估计驾驶员接受订单的概率。我们用logistic回归来估计概率。为了进一步提高用户的体验，我们开发了一个目的地预测模型来预测用户启动应用程序时的目的地列表。基于用户的出发时间、出发地点的纬度和经度等历史数据，利用贝叶斯框架对问题进行了描述。Didi Chuxing应用程序的实验结果表明，我们提出的订单调度模型在成功率这一订单调度系统中最重要的指标方面明显优于现有模型。此外，该模型在用户等待时间、取货距离、平均拆线时间、取消率和车队利用率等指标上都有较好的性能。实验结果也表明，我们的目的地预测方法优于基线模型。

今后，我们将从以下几个方面进一步研究一些有趣的问题：（1）所提出的订单调度模型中的非凸性问题使得寻找全局最优解变得困难。我们计划识别一个凸代理并开发一个快速优化算法来解决相应的优化问题。（2） 我们将进一步改进目的地预测模型，使得即使用户的历史数据中从未出现过真正的目的地，该模型也能够准确地发现新的目的地。