回文序列检测，Manacher算法详解

　　算法简介:算法的目的是在O(n)的时间复杂度内找到一个字符串中各个字母所在的最大长度的回文串。

此算法用到了一个Rad[]数组的定义，Rad[i]表示回文的半径，即最大的j满足s[i-rad[i],i-1]=s[i+1,i+rad[i]]。

很明显，找到了所有的rad[i],就求出了所有的长度为奇数的回文子串，至于偶数的怎么求,最后再讲.

　　假设现在求出了rad[1..i-1],现在要求后面的rad值,并且通过前面的操作,得知了当前字符i的rad值至少为j.

现在通过试图扩大j来扫描,求出了rad[i].再假设现在有个指针k,从1循环到rad[i],试图通过某些手段来

求出[i+1,i+rad[i]]的rad值.

　　根据定义,黑色的部分是一个回文子串,两段红色的区间全等，因为之前已经求出了rad[i-k],所以直接用它.

有3种情况：

 

1. rad[i]-k<rad[i-k]

 

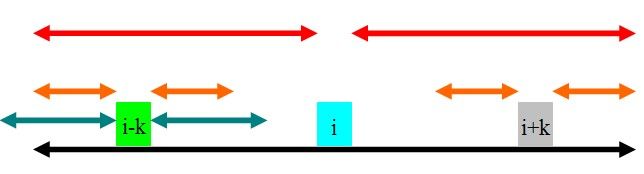
　　如图,rad[i-k]的范围为青色.因为黑色的部分是回文的,且青色的部分超过了黑色的部分,所以rad[i+k]肯定至少为rad[i]-k,

即橙色的部分.那橙色以外的部分就不是了吗?这是肯定的.因为如果橙色以外的部分也是回文的,那么根据青色和红色部分的

关系,可以证明黑色部分再往外延伸一点也是一个回文子串,这肯定不可能,因此rad[i+k]=rad[i]-k.为了方便下文,

这里的rad[i+k]=rad[i]-k=min(rad[i]-k,rad[i-k]).

 

2. rad[i]-k>rad[i-k]

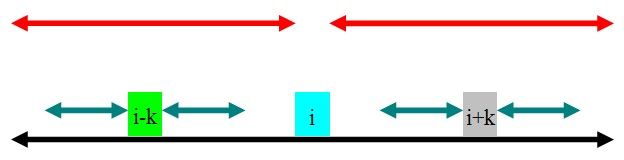
　　如图,rad[i-k]的范围为青色.因为黑色的部分是回文的,且青色的部分在黑色的部分里面,根据定义,很容易得出:rad[i+k]=rad[i-k].

为了方便下文,这里的rad[i+k]=rad[i-k]=min(rad[i]-k,rad[i-k]).

　　根据上面两种情况,可以得出结论:当rad[i]-k!=rad[i-k]的时候,rad[i+k]=min(rad[i]-k,rad[i-k]).

 

3. rad[i]-k==rad[i-k]

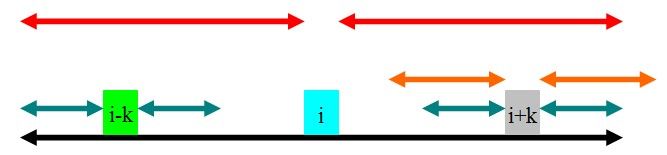
　　如图,通过和第一种情况对比之后会发现,因为青色的部分没有超出黑色的部分,所以即使橙色的部分全等,

也无法像第一种情况一样引出矛盾,因此橙色的部分是有可能全等的,但是,根据已知的信息,我们不知道橙色的部分是多长,

因此就把i指针移到i+k的位置,j=rad[i-k](因为它的rad值至少为rad[i-k]),等下次循环的时候再做了.

 

　　对于长度为偶数的回文子串，一种比较好的方法就是在原来的串中每两个字符之间加入一个特殊字符,再做.

如:aabbaca,把它变成a#a#b#b#a#c#a,这样的话,无论原来的回文子串长度是偶数还是奇数,现在都变成奇数了.

 1 #include <iostream>

 2 #include <string>

 3 using namespace std;

 4 

 5 const int maxnum = 1000000;

 6 

 7 int rad[maxnum*2+1];

 8 

 9 int max(int a, int b)

10 {

11     if (a > b) return a;

12     else return b;

13 }

14 

15 int min(int a, int b)

16 {

17     if (a < b) return a;

18     else return b;

19 }

20 int manacher(string str)

21 {

22     string s;

23     int n = str.size();

24     int ans = 0;

25     int i, j, k;

26     for (i = 0; i < n; i++)

27     {

28         s += '#';

29         s += str[i];

30     }

31     s += '#';

32 

33     n = (n << 1) + 1;

34     i = 0;

35     j = 1;

36     while (i < n)

37     {

38         while (i - j >= 0 && i + j < n && s[i - j] == s[i + j])

39             j++;

40         rad[i] = j - 1;

41         k = 1;

42         while (k <= rad[i] && rad[i] - k != rad[i - k])

43         {

44             rad[i + k] = min(rad[i - k], rad[i] - k);

45             k++;

46         }

47         i += k;

48         j = j - k;

49     }

50     for (i = 0; i < n; i++)

51         ans = max(ans, rad[i]);

52     return ans;

53 }

54 

55 int main()

56 {

57     string str;

58     cin >> str;

59     cout << manacher(str) << endl;

60     

61     return 0;

62 }