图像处理 空域增强

资源是可以掠夺的，要么永远缩在后面用那怯弱的目光看着别人在舞台上光彩夺目，要么咬着牙狠狠的提升自己的实力，在将来的某一天一鸣惊人，受万众瞩目。——《全职法师》

前言

• 图像增强：改变图像像素的灰度值，以改变图像灰度的动态范围，增强图像的对比度。
  • 增强的目的：
    • 改善图像的视觉效果，提高清晰度；
    • 将图像转换为一种更适合于人或机器分析处理的形式。
• 空域法：直接对图像的像素灰度值进行操作。
• 频域法：在变换域中，对图像的变换值进行操作。
• 空域增强分为：点操作和模板操作（邻域操作）。

概念

• 在图像处理中，空域是指像素组成的空间。
• 图像的空域增强技术是指直接作用于图像像素的增强技术。

空域增强的模型

模型	说明
$$g(x,y)=E_H[f(x,y)]$$	$f(x,y)$为原始图像， $g(x,y)$为增强后的图像， $E_H$为增强操作，仅定义在每个像素点$(x,y)$上。

基于像素的空域增强

操作类型	操作	说明
像素点操作	$$g(x,y)=P_{xy}[f(x,y)]$$	根据单个像素的灰度，或者像素的位置来改变该像素的灰度。
几何操作	$(x^{\prime },y^{\prime })=M(x,y)$	仅根据一个像素的位置，$M$为几何隐射函数。

基于模板的空域增强

操作	说明
$$t=E_H[s,n(S)]$$	其中，$E_H$定义在像素$(x,y)$的某个邻域上，$s$，$t$分别为原始图像$f$和结果图像$g$在$(x,y)$初的灰度值，$n(s)$为原始图像$f$在以$(x,y)$为中心的领域内像素的灰度值。

算术运算

对图像进行的算术运算是逐像素进行的，即两幅图像的对应位置的像素间进行算术运算。

加法

• 可以用于去除图像噪声（叠加多张受噪声污染程度不同的图片，取均值弱化噪声对图片的影响）
  • 若噪声具有互不相关、零均值的统计特性。
  • 原始图像：$f(x,y)$，随机噪声：$e(x,y)$
  • 噪声污染图像：$g(x,y)=f(x,y)+e(x,y)$
  • $M$幅噪声污染图像相加求平均：$$\bar{g}(x,y)=\frac{1}{M}\sum _{i=1}^M{g}_i(x,y)$$
• 生成图像叠加效果

减法

• 数字剪影
• 森林火灾
• 运动跟踪和检测
• 污染检测
• 伪印章鉴别

乘法

• 用二值模板图像与原图像做乘法进行图像的局部显示。

灰度映射

• 动态范围：是指图像中从暗到亮的变化范围。
• 动态范围对人视觉的影响：
  • 由于人眼所可以分辨的灰度的变化范围是有限的，所以当动态范围太大的时候，很高的亮度值把暗区的信号都掩盖了。

原理：按照某种映射规则或变换函数，将图像中的每个像素点的灰度值转化成另一灰度值。

典型灰度映射

名称	作用	模型描述	表达式
图像求反	将原图灰度值翻转，黑变白、白变黑。	假设原始图像任意像素点的灰度值为$s$，经过灰度映射后的灰度值为$t$，且灰度映射前后的灰度值取值范围为$[0,L-1]$	$$t=(L-1)-s$$
分段线性增强	增强感兴趣的灰度区域，相对抑制不感兴趣的灰度区域。	利用分段函数增强图像细节之间的对比度。
对数变换	原图动态范围太大，超出某些显示设备的允许动态范围，需要压缩其动态范围。	常采用对数变换实现动态范围的压缩。	$$t=Clog(1+|s|)$$
幂律(伽马)变换	与对数变换类似，部分$\gamma$值的幂律曲线将较窄范围的暗色输入值映射为较宽范围的输出值；相反地，对于输入高灰度值也成立。	$C$和$\gamma$为正常数，注意$\gamma >1$和$\gamma <1$的幂律变换效果完全相反。	$$t=c\times s^{\gamma }$$
灰度切割	增强特定范围的对比度，用来突出图像中特定灰度范围的亮度。	对感兴趣的灰度级以较大的灰度值显示，其它的为较小的灰度级显示。	$$t=\{\begin{array}{ll}{t}_2& {\text{S}}_1\le S\le S_2\\ t_1& \text{其}他\end{array}$$
		对感兴趣的灰度级以较大的灰度值显示，其它不变。	$$t=\{\begin{array}{ll}{t}_2& {\text{S}}_1\le S\le S_2\\ S& \text{其}他\end{array}$$
阈值化处理	阈值化处理，也即阈值变换，目的在于将感兴趣的物体从背景中分离出来。	阈值化处理需要指定一个阈值$threshold$，根据这个阈值修改图像的像素值，最终产生一个黑白图像。	$$t=\{\begin{array}{ll}0& \text{S}<S_1\\ L-1& \text{S}\ge S_1\end{array}$$
位图切割	假设图像的像素由$8$位（比特）表示其灰度值，则图像可以看成由$8$个单独的1比特平面（简称为位面）组成，其范围从最低有效位的位面0 到最高有效位的位面7。每个位面均为二值图像，且位面图像中像素的灰度值等于相应有效位的取值。位面$0$表示最低位面，仅包含图像中像素的最低位；位面$7$表示最高位面，仅包含图像中像素的最高位。	将图像各像素的灰度值除以各有效位的权值$2^i$（$i$为有效位的序数，从0计数）。如果商的整数部分为奇数，则该灰度值在相应位面中映射为 1；如果商的整数部分为偶数，则映射为 0，即可得到每个位面的二值图像。	$$t=\{\begin{array}{ll}1& \text{f}loor(像素值/2^i)=奇数（i，位面序数）\\ 0& \text{f}loor(像素值/2^i)=偶数\end{array}$$

直方图

• 图像的灰度直方图是二维图像的灰度分布统计，是一个1-D的离散函数。
• $h(k)$是$f(x,y)$中具有灰度值$k$的像素的个数。$$h(k)=n_{k}k=0,1,\dots L-1$$
• 直方图反映图像中不同灰度出现的次数，不反映某一灰度值像素所在位置，不具有空间特性。

知识点	说明
说明	直方图是图像的一种统计表达，反映了图像中像素的灰度值的分布情况。
基本思想	把图像的直方图变换为均匀分布的形式，以此增强动态范围偏小的图像的反差，从而达到对比度增强。

归一直方图

$$p(S_k)=\frac{n_k}{n}{S}_k=\frac{k}{L-1},0\le S_k\le 1$$

• $k$为图像像素点的灰度级
• $L$为灰度级【计算公式为$2^i$】，最小一般为$8$
• $p(S_k)$为归一化灰度级$S_k$在图像上出现的概率（频度）
• $n_k$为图像中灰度级为$k$的像素的个数，$k=0,1,\dots ,L-1$
• $n$为图像所有像素的数量
• $S_k$为图像第$k$个灰度级的归一化值（归一化灰度级）

累积直方图

$$H(k)=\sum _{i=0}^k{n}_i$$

• $k$为图像像素点的灰度级，$k=0,1,\dots ,L-1$。
• $L$为灰度级【计算公式为$2^i$】，最小一般为$8$。
• $H(k)$表示图像中灰度级小于或者等于$k$的像素点的数量。
• $n_i$表示图像中灰度级等于$i$的像素点的数量。

归一化累积直方图

$$H(S_k)=\sum _{i=0}^{k}p(S_i)$$

• $k$为图像像素点的灰度级，$k=0,1,\dots ,L-1$。
• $H(S_k)$表示小于或等于$S_k$的归一化灰度级在图像中出现的总概率
• $S_i$表示第级$i$归一化灰度级
• $p(S_i)$表示归一化灰度级$S_i$在图像中出现的概率

直方图均衡化原理

直方图的均衡化用于增强动态范围偏小的图像的反差。直方图均衡化把原始图直方图变换为整个灰度范围内均匀分布的形式，使图中具有近似灰度且占有大量像素的区域的灰度范围展宽，使大区域中微小灰度变化显现出来。增加像素灰度值的动态范围，从而达到增强图像整体对比度的效果。

• 为了实现均衡化，增强函数$E_H(S)$需要满足两个条件：
  • $E_H(S)$必须为单值单增函数，其中$0\le S\le L-1$，各灰度级在变换后扔保持排序次序。
  • $0\le E_H(S)\le L-1$，变换前后灰度值动态范围一致。
  • 反变换也应该满足以上两个条件。
• 累积分布函数（$CDF$）满足以上两条件并能将输入值$S$的分布转换为输出值$t$的均匀分布。$$t_k=E_H(S_k)=\sum _{i=0}^k\frac{n_i}{n}=\sum _{i=0}^{k}p(S_i)0\le t_k\le 1,0\le S_k\le 1$$
  • $t_k$，单值单增函数。

实现过程

1. 计算源图像的归一化直方图$$\begin{gathered} p(S_k)=\frac{n_k}{n},k=0,1,\dots ,L-1 \\ {S}_k=\frac{k}{L-1},0\le S_k\le 1 \end{gathered}$$
2. 计算源图像的归一化累积直方图$$t_k=H(S_k)=\sum _{i=0}^{k}p(S_i)$$
3. 采用$t_k^{\prime }=int[(L-1)t_k+0.5]$将$t_k$扩展到$[0,L-1]$范围内，得到直方图均衡化后的灰度值。
4. 依据$t_k^{\prime }$重新计算$n_{t_k^{\prime }}$和$p(t_k^{\prime })=\frac{n_{t_k^{\prime }}}{n}$的值。即将原始图像的直方图映射到规定的直方图。

说明：该函数$t_k^{\prime }=int[(L-1)t_k+0.5]$是用户指定的需要的规定化的函数，主要用于得到特殊的增强功能。这个函数可以自行替换，只需要让替换后的公式符合$[0,L-1]$的要求即可。

空域滤波增强

空域滤波器是在图像空间中借助模板进行邻域操作完成的。

滤波产生一个新像素，新像素的坐标等于邻域中心的坐标，像素的值是滤波操作的结果。

滤波器的中心访问输入图像中的每个像素，就生成了滤波后的图像。

如果在图像上执行的是线性操作，则称该滤波器为线性空间滤波器；反之，为非线性空间滤波器。

分类

分类	作用	说明
平滑线性滤波	模糊处理和减弱噪声。	带来图像边缘模糊的负面效应。
锐化滤波	减弱或者消除图像中的低频分量，但不影响高频分量。低频分量对应图像中灰度值缓慢变化的区域，因而与图像的整体特性（整体对比度和平均灰度值等）有关。	可使图像反差增加，边缘明显。增强被模糊的细节或者目标的边缘。

线性滤波实现原理

【模板卷积】使用大小为$m\times n$的滤波器对大小为$M\times N$的图像进行线性空间滤波，对于图像中的任意一点$(x,y)$，滤波器的响应$g(x,y)$是滤波器系数与该滤波器包围的图像像素的乘积之和，可由下式表示：$$g(x,y)=\sum _{s=-a}^a\sum _{t=-b}^{b}w(s,t)f(x+s,y+t),a=\frac{m-1}{2},b=\frac{n-1}{2},a\in N^{\ast },b\in N^{\ast }$$

其中，$w(s,t)$为滤波器系数，且滤波器中心系数$w(0,0)$对准位置为$(x,y)$的像素。

注意：使用奇数尺寸的滤波器可简化索引，且更为直观，因为滤波器的中心落在整数值上。

算法步骤：

• 将滤波器在图像中漫游，并将滤波器中心与图像中某个像素位置重合；
• 将滤波器中的各个系数与滤波器所覆盖的各对应像素的灰度值相乘；
• 将所有乘积相加；
• 将上述运算结果（滤波器的输出响应）赋给图像中对应滤波器中心位置的像素。
• 计算公式如下：$$\begin{gathered} g(x,y)=w(-1,-1)f(x-1,y-1)+w(-1,0)f(x-1,y)+w(-1,1)f(x-1,y+1) \\ +w(0,-1)f(x,y-1)+w(0,0)f(x,y)+w(0,1)f(x,y+1) \\ +w(1,-1)f(x+1,y-1)+w(1,0)f(x+1,y)+w(1,1)f(x+1,y+1) \end{gathered}$$

线性滤波器分类

种类	公式	说明	模板
邻域平均	$$\begin{gathered} g(x,y)=\frac{1}{mn}\sum _{(x,y)\in S}f(x,y) \\ \text{S：邻域，mn：邻域S像素个数} \end{gathered}$$	图像会产生模糊，邻域越大，模糊越厉害。
加权平均	$$\begin{gathered} g(x,y)=\sum _{s=-a}^a\sum _{t=-b}^{b}w(s,t)f(x+s,y+t), \\ a=\frac{m-1}{2},b=\frac{n-1}{2},a\in N^{\ast },b\in N^{\ast } \end{gathered}$$

非线性平滑滤波器

统计排序滤波器是一种非线性空间滤波器。

统计排序滤波器的响应以滤波器包围的图像区域中所包含的像素的排序为基础，然后使用统计排序结果所决定的值代替中心像素的值。

统计排序滤波器具备优秀的去噪能力，而且比相同尺寸的线性平滑滤波器的模糊程度明显要低。

非线性平滑滤波器分类

分类	公式	说明
中值滤波器		使用像素邻域内灰度的中值（在中值计算中包括原像素值）代替该像素的值。中值滤波器的主要功能是使拥有不同灰度的像素点看起来更接近于它的相邻点（去除那些相对于其邻域像素更亮或更暗孤立像素）。
百分比滤波器	$$\begin{gathered} g_{max}(x,y)=\underset{(s,t)\in N(x,y)}{\max }[f(s,t)] \\ {g}_{min}(x,y)=\underset{(s,t)\in N(x,y)}{\min }[f(s,t)] \end{gathered}$$	“椒”噪声有较低的灰度值，用最大值滤波器有较好的效果；“盐”噪声的灰度值较高，用最小值滤波器。
中点滤波器	$$\begin{gathered} g_{mid}(x,y)=\frac{1}{2}\{\underset{(s,t)\in N(x,y)}{\max }[f(s,t)]+\underset{(s,t)\in N(x,y)}{\min }[f(s,t)]\} \\ =\frac{1}{2}[g_{max}(x,y)+g_{min}(x,y)] \end{gathered}$$	中点滤波器以滤波器所覆盖的像素邻域的最大灰度值和最小灰度值的均值作为输出值。中点滤波器结合了排序统计和求平均，对于高斯和均匀分布随机噪声有较好效果

非线性锐化滤波器

锐化处理的主要目的是突出图像中灰度的过渡部分

图像的锐化处理可以用空间微分来完成（微分算子的响应强度与图像在该点的突变程度成正比）。

分类	说明	公式
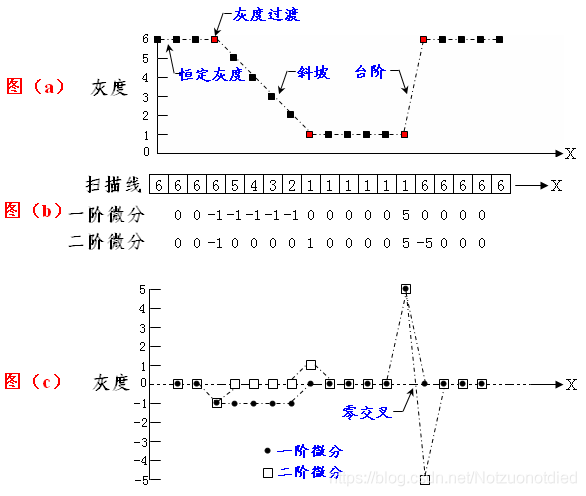
基于一阶微分的锐化滤波器	在恒定灰度区域的一阶微分值为零；在灰度台阶或斜坡起点处一阶微分值非零；沿着斜坡的一阶微分值非零。	$$\frac{\partial f}{\partial x}=f(x+1)-f(x),\text{一维离散函数f(x)}$$如果是二维的数字图像f(x, y)，可以沿着空间轴处理偏微分。
基于二阶微分的锐化滤波器	在恒定灰度区域的二阶微分值为零；在灰度台阶或斜坡的起点处二阶微分值非零；沿着斜坡的二阶微分值为零。	$$\frac{{\partial }^{2}f}{{\partial }^{2}x}=f(x+1)+f(x-1)-2f(x),\text{一维离散函数f(x)}$$如果是二维的数字图像f(x, y)，可以沿着空间轴处理偏微分。

一阶微分处理通常会产生较宽的边缘，因为数字图像中对的边缘在灰度上类似于斜坡过渡，而沿着斜坡的一阶微分非零。二阶微分处理对细节有较强的响应（如细线和孤立点），通常产生由零分开的一个像素宽的双边缘。大多数应用中，对图像增强而言，因为二阶微分对细节的增强能力比一阶微分好。

基于一阶微分的锐化滤波器——梯度算子

在图像处理中，一阶微分是用梯度幅值来实现的。对于图像$f$，在任意坐标$(x,y)$上的梯度$\nabla f$定义为二维变量。

$$\nabla f={\left[G_x{G}_y\right]}^T={\left[\frac{\partial f}{\partial x}\frac{\partial f}{\partial y}\right]}^T$$

梯度的幅值$|\nabla f|$定义为：

$$|\nabla f|=\sqrt{G_x^2+G_y^2}=\sqrt{{\left(\frac{\partial f}{\partial x}\right)}^2+{\left(\frac{\partial f}{\partial y}\right)}^2}$$

其实，在实际应用中，为了简化计算，采用绝对值替代平方和开方运算：

$$|\nabla f|=|G_x|+|G_y|=\left|\frac{\partial f}{\partial x}\right|+\left|\frac{\partial f}{\partial y}\right|$$

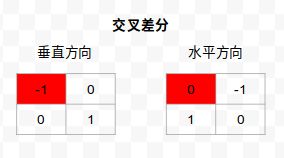
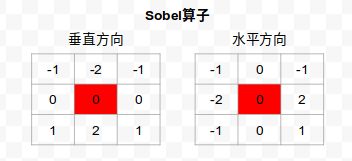
梯度算子分类

注意：所有的模板系数之和为零。

种类	公式	模板
直接差分	$$G_x=f(x+1,y)-f(x,y)$$$$G_y=f(x,y+1)-f(x,y)$$
交叉差分	$$G_x=f(x+1,y+1)-f(x,y)$$$$G_y=f(x+1,y)-f(x,y+1)$$
Sobel算子	$$\begin{gathered} G_x=f(x+1,y-1)+2f(x+1,y)+f(x+1,y+1) \\ -f(x-1,y-1)-2f(x-1,y)-f(x-1,y+1) \end{gathered}$$$$\begin{gathered} G_y=f(x-1,y+1)+2f(,y+1)+f(x+1,y+1) \\ -f(x-1,y-1)-2f(x,y-1)-f(x+1,y-1) \end{gathered}$$

梯度值正比于邻近像素灰度值的差分，因此在图像变化缓慢区域，其值很小，而在轮廓等变化快的部分其值很大，这就是图像经过梯度计算可使其细节清晰从而达到锐化目的的实质。

基于二阶微分的锐化滤波器——拉普拉斯算子

拉普拉斯算子比较适用于改善因光线的漫反射造成的图像模糊。

数字图像$f(x,y)$的拉普拉斯变换定义为：$${\nabla }^{2}f=\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}$$

因此：

$$\frac{{\partial }^{2}f}{\partial x^2}=f(x+1,y)+f(x-1,y)-2f(x,y)$$

$$\frac{{\partial }^{2}f}{\partial y^2}=f(x,y+1)+f(x,y-1)-2f(x,y)$$

综上可得：

$${\nabla }^{2}f=\left[f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)\right]-4f(x,y)$$

拉普拉斯算子模板：

拉普拉斯算子强调图片中灰度的突变，同时降低灰度慢变化的区域，使用拉普拉斯变换对图像进行增强的基本方法：

$$g(x,y)=\{\begin{array}{ll}f(x,y)-{\nabla }^{2}f& \text{若}拉普拉斯模板中心系数为负\\ f(x,y)+{\nabla }^{2}f& \text{若}拉普拉斯模板中心系数为正\end{array}$$

上述式子可以描述为：将原始图像和拉普拉斯图像叠加在一起，以增强原始图像的细节，同时又保护了原始图像的背景信息。

附录

• 空域图像增强 PPT