pytorch稀疏矩阵
因为我是做GNN的,在图中存储邻接矩阵时如果使用矩阵是相当浪费的,因为矩阵中绝大多数元素都是0,这时我们可以使用稀疏矩阵来存储数据,使用稀疏矩阵之后,不仅能节省内存,而且pytorch为这种矩阵的运算进行了优化,我实验发现在涉及到矩阵相乘的地方使用稀疏矩阵可以大大提高计算性能:
![]()
1. coo存储格式
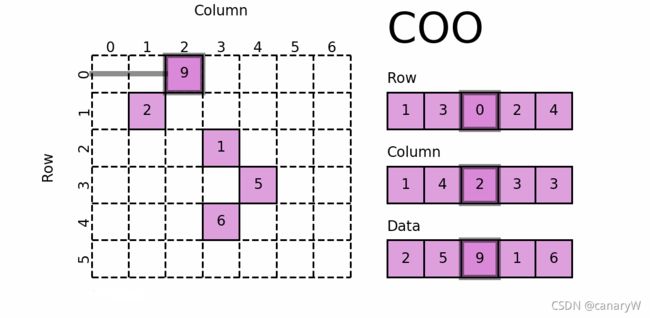
在上图中,因为绝大多数元素都是0,因此我们只需要三个向量就能存储全部信息:非零元素的行下标,非0元素的列下标,非0元素的值。
2. torch sparse
此处提供的API为:torch.sparse_coo_tensor(index,value,size)
函数接收三个参数,返回一个紧密矩阵
参数:
- index:shape为[2,n],代表着行下标向量和列下标向量
- value:shape为[n],代表着非零元素的值
- size:代表着稀疏矩阵的shape
栗子:
>>> i = [[0, 1, 1],
[2, 0, 2]]
>>> v = [3, 4, 5]
>>> s = torch.sparse_coo_tensor(i, v, (2, 3))
>>> s
tensor(indices=tensor([[0, 1, 1],
[2, 0, 2]]),
values=tensor([3, 4, 5]),
size=(2, 3), nnz=3, layout=torch.sparse_coo)
>>> s.to_dense()
tensor([[0, 0, 3],
[4, 0, 5]])
我觉得最实用的API:torch1.9支持将一个矩阵直接转为coo_matrix:Tensor.to_sparse()
>>> s=torch.tensor([[0, 0, 3],
[4, 0, 5]])
>>> s.to_sparse()
tensor(indices=tensor([[0, 1, 1],
[2, 0, 2]]),
values=tensor([3, 4, 5]),
size=(2, 3), nnz=3, layout=torch.sparse_coo)
3. torch中稀疏矩阵运算
- 可以强制类型转换,与正常矩阵进行乘积,加法等矩阵操作
>>> s=s.float()
>>> a=torch.ones((3,2))
torch.tensor([[1,1],
[1,1],
[1,1])
>>> torch.mm(s,a)
tensor([[3., 3.],
[9., 9.]])
如果进行稀疏矩阵*紧密矩阵,推荐使用torch.spmm(),这样更加直观
但是在实验过程转换,我发现tensor中的一些API在稀疏矩阵中还未实现:

很需要注意的一点:
pytorch目前只支持稀疏矩阵*紧密矩阵,也就是说,在torch.mm()中,第一个参数必须是稀疏矩阵,而第二个参数是正常的Tensor。