HBU_神经网络与深度学习 实验2 pytorch入门
目录
- 写在前面的一些内容
- 一、张量与算子的概念
- 二、张量的操作
-
- 1. 创建张量
-
- (1)指定数据创建张量
- (2)指定形状创建张量
- (3)指定区间创建张量
- 2. 张量的属性
-
- (1)张量的形状
- (2)形状的改变
- (3)张量的数据类型
- (4)张量的设备位置
- 3. 张量与Numpy数组转换
-
- (1)张量转化为numpy数组
- (2)numpy数组转化为张量
- 4. 张量的访问
-
- (1)索引和切片
- (2)访问张量
- (3)修改张量
- 5. 张量的运算
-
- (1)数学运算
- (2)逻辑运算
- (3)矩阵运算
- (4)广播机制
- 三、数据预处理
-
- 1. 读取数据集 house_tiny.csv、boston_house_prices.csv、Iris.csv
- 2. 处理缺失值
- 3. 转换为张量格式
- 四、实验总结
写在前面的一些内容
- 本文为HBU_神经网络与深度学习实验(2022年秋)实验2的实验报告,此文的基本内容参照 神经网络与深度学习:案例与实践 - 第1章:实验基础 ,检索时请按对应题号进行检索。
- 本实验编程语言为Python 3,使用Pycharm进行编程,所使用解释器为Python 3.10 (pytorch).
- 本实验报告目录标题级别顺序:一、1. (1)
- 水平有限,难免有误,如有错漏之处敬请指正。
一、张量与算子的概念
1. 张量
张量概念是矢量概念的推广,矢量是一阶张量。张量是一个可用来表示在一些矢量、标量和其他张量之间的线性关系的多线性函数。[1] 张量 - 百度百科
张量是数据的一种存储方式,向量、矩阵等可以称为1阶或2阶张量,同理张量也可以表示n阶多维numpy数组。
下图为 [2]不同维度的张量可视化表示 。
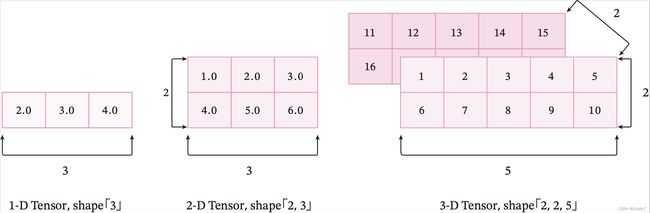
2.算子
算子是一个函数空间到函数空间上的映射O:X→X。广义上的算子可以推广到任何空间,如内积空间等。[3] 算子 - 百度百科
如果我们实现每个基础函数的前向函数和反向函数,就可以非常方便地通过这些基础函数组合出复杂函数,并通过链式法则反向计算复杂函数的偏导数。 在深度学习框架中,这些基本函数的实现称为算子(Operator,Op)。有了算子,就可以像搭积木一样构建复杂的模型。[4]
二、张量的操作
进行实验前,我们需要先导入torch包。
import torch
1. 创建张量
(1)指定数据创建张量
# 一维张量
a = torch.tensor([2.0, 3.0, 4.0])
print("一维张量:", a)
# 二维张量
b = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
print("二维张量:", b)
# 多维张量
c = torch.tensor([[[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]],
[[11, 12, 13, 14, 15], [16, 17, 18, 19, 20]]])
print("多维张量:", c)
代码执行结果:
一维张量: tensor([2., 3., 4.])
二维张量: tensor([[1., 2., 3.],
[4., 5., 6.]])
多维张量: tensor([[[ 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10]],
[[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20]]])
显然,通过给定Python列表数据,可以创建任意维度的张量。需要注意的是,张量在任何一个维度上的元素数量必须相等。
下面尝试定义一个在不同维度上元素数量不等的张量。
# 尝试定义在不同维度上元素数量不等的张量
d = torch.tensor([[1.0, 2.0], [4.0, 5.0, 6.0]])
print(d)
代码执行结果(抛出异常):
Traceback (most recent call last):
File "C:\Users\...\DeepLearningExperiment\EX2.py", line ..., in <module>
d = torch.tensor([[1.0, 2.0],[4.0, 5.0, 6.0]])
ValueError: expected sequence of length 2 at dim 1 (got 3)
显然,读取时读取到第二维有3个元素,与第一维不符,所以抛出元素数量不等的异常。
(2)指定形状创建张量
如果要创建一个指定形状、元素数据相同的张量,可以调用函数zeros, ones, full进行张量创建。
m, n = 2, 3
# 创建数据全为0,形状为[m, n]的张量
a = torch.zeros([2, 3])
print('zeros Tensor:', a)
# 创建数据全为1,形状为[m, n]的张量
b = torch.ones([2, 3])
print('ones Tensor:', b)
# 创建数据全为指定值,形状为[m, n]的张量,此处我们指定数据为10
c = torch.full([2, 3], 10)
print('full Tensor:', c)
代码执行结果:
zeros Tensor: tensor([[0., 0., 0.],
[0., 0., 0.]])
ones Tensor: tensor([[1., 1., 1.],
[1., 1., 1.]])
full Tensor: tensor([[10, 10, 10],
[10, 10, 10]])
(3)指定区间创建张量
如果要在指定区间内创建张量,可以调用函数arange, linspace进行张量创建。
# 创建以步长step均匀分隔数值区间[start, end)的一维张量
a = torch.arange(start=1, end=5, step=1)
print('arange Tensor:', a)
# 创建以元素个数num均匀分隔数值区间[start, stop]的张量
b = torch.linspace(start=1, end=5, steps=5)
print('linspace Tensor:', b)
代码执行结果:
arange Tensor: tensor([1, 2, 3, 4])
linspace Tensor: tensor([1., 2., 3., 4., 5.])
2. 张量的属性
(1)张量的形状
| 属性 | 功能 |
|---|---|
| ndim | 张量的维度 |
| shape | 张量每个维度上元素的数量 |
| shape[n] | 张量第n维的大小(n=-1时表示最后一维的大小) |
| numel | 张量中全部元素的个数 |
a = torch.ones([2, 3, 4, 5])
print("维度大小:", a.ndim)
print("张量中各个维度上元素的数量:", a.shape)
print("张量第一维的大小:", a.shape[0])
print("张量最后一维的大小:", a.shape[-1])
print("张量中元素的个数:", a.numel())
上述实验代码中的四维张量([5]形状为[2, 3, 4, 5])如下图所示。
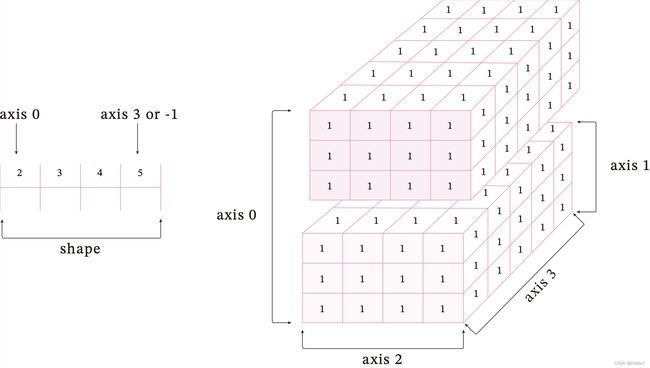
代码执行结果:
维度大小: 4
张量中各个维度上元素的数量: torch.Size([2, 3, 4, 5])
张量第一维的大小: 2
张量最后一维的大小: 5
张量中元素的个数: 120
(2)形状的改变
调用reshape函数可以保持在输入数据不变的情况下,改变数据形状。
# 定义一个shape为[3,2,5]的三维张量
A = torch.tensor([[[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10]],
[[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20]],
[[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30]]])
print("the shape of a:", A.shape)
# 设置reshape为[2,5,3]
b = A.reshape(2, 5, 3)
print("After reshape:", b)
# 将原张量reshape为一维张量并输出张量的大小
c = A.reshape([-1])
print("After reshape:", c.shape[0])
代码执行结果:
the shape of A: torch.Size([3, 2, 5])
After reshape: tensor([[[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12],
[13, 14, 15]],
[[16, 17, 18],
[19, 20, 21],
[22, 23, 24],
[25, 26, 27],
[28, 29, 30]]])
After reshape: 30
(3)张量的数据类型
调用dtype函数来查看张量的数据类型。
a = torch.tensor([1, 2, 3])
print("张量a的数据类型:", a.type())
b = torch.tensor([4.0, 5.0, 6.0])
print("张量b的数据类型:", b.type())
代码执行结果:
张量a的数据类型: torch.LongTensor
张量b的数据类型: torch.FloatTensor
(4)张量的设备位置
使用device属性来查看张量的设备位置。
a = torch.tensor([1, 2, 3])
print("张量a的设备位置:", a.device)
代码执行结果:
张量a的设备位置: cpu
该实验使用CPU版本的pytorch运行,故输出设备位置为cpu.
3. 张量与Numpy数组转换
(1)张量转化为numpy数组
import numpy
a = torch.Tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
b = a.numpy()
print("张量a转化为数组:", b)
代码执行结果:
张量a转化为数组: [[1. 2. 3.]
[4. 5. 6.]
[7. 8. 9.]]
(2)numpy数组转化为张量
import numpy
a = numpy.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
b = torch.Tensor(a)
print("数组a转化为张量:", b)
代码执行结果:
数组a转化为张量: tensor([[1., 2., 3.],
[4., 5., 6.],
[7., 8., 9.]])
4. 张量的访问
(1)索引和切片
我们可以通过索引或切片方便地访问或修改张量。飞桨使用标准的Python索引规则与Numpy索引规则,具有以下特点:
1 基于0−n的下标进行索引,如果下标为负数,则从尾部开始计算。
2 通过冒号“:”分隔切片参数start:stop:step来进行切片操作,也就是访问start到stop范围内的部分元素并生成一个新的序列。其中start为切片的起始位置,stop为切片的截止位置,step是切片的步长,这三个参数均可缺省。[4]
(2)访问张量
与numpy相同,按位置访问即可。
(以二维张量为例)
a = torch.tensor([[0, 1, 2, 3],
[4, 5, 6, 7],
[8, 9, 10, 11]])
print("张量a:", a)
print("第一行:", a[0])
print("第一行:", a[0, :])
print("第一列:", a[:, 0])
print("最后一列:", a[:, -1])
print("张量中所有元素:", a[:])
print("第一行第二列的元素:", a[0, 1])
代码执行结果:
张量a: tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
第一行: tensor([0, 1, 2, 3])
第一行: tensor([0, 1, 2, 3])
第一列: tensor([0, 4, 8])
最后一列: tensor([ 3, 7, 11])
张量中所有元素: tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
第一行第二列的元素: tensor(1)
(3)修改张量
与访问张量类似,可以在单个或多个轴上通过索引或切片操作来修改张量。
提醒
慎重通过索引或切片操作来修改张量,此操作仅会原地修改该张量的数值,且原值不会被保存。如果被修改的张量参与梯度计算,将仅会使用修改后的数值,这可能会给梯度计算引入风险。[4]
a = torch.zeros([2, 3])
print('张量a:', a)
# 修改第1维为1
a[0] = 1
print('修改第1维为1:', a)
# 修改第1维为2.1
a[0:1] = 2.1
print('修改第1维为2.1:', a)
# 修改全部Tensor
a[...] = 3
print('修改全部张量元素为3:', a)
代码执行结果:
张量a: tensor([[0., 0., 0.],
[0., 0., 0.]])
修改第1维为1: tensor([[1., 1., 1.],
[0., 0., 0.]])
修改第1维为2.1: tensor([[2.1000, 2.1000, 2.1000],
[0.0000, 0.0000, 0.0000]])
修改全部张量元素为3: tensor([[3., 3., 3.],
[3., 3., 3.]])
5. 张量的运算
(1)数学运算
张量类的基础数学函数如下:
| 函数 | 功能 |
|---|---|
| x + y 和 x.add(y) | 逐元素加 |
| x - y 和 x.subtract(y) | 逐元素减 |
| x * y 和 x.multiply(y) | 逐元素乘 |
| x / y 和 x.divide(y) | 逐元素除 |
| x % y 和 x.mod(y) | 逐元素取余 |
| x ** y 和 x.pow(y) | 逐元素幂 |
| x.abs() | 逐元素取绝对值 |
| x.ceil() | 逐元素向上取整 |
| x.floor() | 逐元素向下取整 |
| x.round() | 逐元素四舍五入 |
| x.exp() | 逐元素计算自然常数为底的指数 |
| x.log() | 逐元素计算x的自然对数 |
| x.reciprocal() | 逐元素求倒数 |
| x.square() | 逐元素计算平方 |
| x.sqrt() | 逐元素计算平方根 |
| x.sin() | 逐元素计算正弦 |
| x.cos() | 逐元素计算余弦 |
| x.max() | 指定维度上元素最大值,默认为全部维度 |
| x.min() | 指定维度上元素最小值,默认为全部维度 |
| x.prod() | 指定维度上元素累乘,默认为全部维度 |
| x.sum() | 指定维度上元素的和,默认为全部维度 |
代码以其中一部分函数举例
a = torch.tensor([-1.0, -2, -4, -8])
print("a =", a)
print("|a| =", a.abs())
print("a + 1 =", a + 1)
print("a - 1 =", a - 1)
print("a * 2 =", a * 2)
print("a / 2 =", a / 2)
print("a % 2 =", a % 2)
print("a ** 2 =", a ** 2)
print("(-a) ** 0.5 =", (-a) ** 0.5)
代码执行结果:
a = tensor([-1., -2., -4., -8.])
|a| = tensor([1., 2., 4., 8.])
a + 1 = tensor([ 0., -1., -3., -7.])
a - 1 = tensor([-2., -3., -5., -9.])
a * 2 = tensor([ -2., -4., -8., -16.])
a / 2 = tensor([-0.5000, -1.0000, -2.0000, -4.0000])
a % 2 = tensor([1., -0., -0., -0.])
a ** 2 = tensor([ 1., 4., 16., 64.])
(-a) ** 0.5 = tensor([1.0000, 1.4142, 2.0000, 2.8284])
(2)逻辑运算
张量类的逻辑运算函数如下:
| 函数 | 功能 |
|---|---|
| x.isfinite() | 判断张量中元素是否是有限的数字,即不包括inf与nan |
| x.equal_all(y) | 判断两个张量的全部元素是否相等,并返回形状为[1]的布尔类张量 |
| x.equal(y) | 判断两个张量的每个元素是否相等,并返回形状相同的布尔类张量 |
| x.not_equal(y) | 判断两个张量的每个元素是否不相等 |
| x.less_than(y) | 判断张量x的元素是否小于张量y的对应元素 |
| x.less_equal(y) | 判断张量x的元素是否小于或等于张量y的对应元素 |
| x.greater_than(y) | 判断张量x的元素是否大于张量y的对应元素 |
| x.greater_equal(y) | 判断张量x的元素是否大于或等于张量y的对应元素 |
| x.allclose(y) | 判断两个张量的全部元素是否接近 |
(3)矩阵运算
张量类还包含了矩阵运算相关的函数,如矩阵的转置、范数计算和乘法等。
| 函数 | 功能 |
|---|---|
| x.t() | 矩阵转置 |
| x.transpose([1, 0]) | 交换第0维与第1维的顺序 |
| x.norm(‘fro’) | 矩阵的弗罗贝尼乌斯范数 |
| x.dist(y, p=2) | 矩阵(x-y)的2范数 |
| x.matmul(y) | 矩阵乘法 |
有些矩阵运算中也支持大于两维的张量,比如matmul函数,对最后两个维度进行矩阵乘。比如x是形状为[j,k,n,m]的张量,另一个y是[j,k,m,p]的张量,则x.matmul(y)输出的张量形状为[j,k,n,p]。
(4)广播机制
以下内容标记为本人尚未完全理解的内容,因此所有文字均摘自 神经网络与深度学习:案例与实践 - 第1章:实验基础
飞桨的一些API在计算时支持广播(Broadcasting)机制,允许在一些运算时使用不同形状的张量。通常来讲,如果有一个形状较小和一个形状较大的张量,会希望多次使用较小的张量来对较大的张量执行某些操作,看起来像是形状较小的张量首先被扩展到和较大的张量形状一致,然后再做运算。
飞桨的广播机制主要遵循如下规则(参考Numpy广播机制):
1)每个张量至少为一维张量。
2)从后往前比较张量的形状,当前维度的大小要么相等,要么其中一个等于1,要么其中一个不存在。[4]
x = torch.ones([2, 3, 4])
y = torch.ones([2, 3, 4])
z = x + y
print('广播两个相同形状的张量:', z.shape)
x = torch.ones([2, 3, 1, 5])
y = torch.ones([3, 4, 1])
# 从后往前依次比较:
# 第一次:y的维度大小是1
# 第二次:x的维度大小是1
# 第三次:x和y的维度大小相等,都为3
# 第四次:y的维度不存在
# 所以x和y是可以广播的
z = x + y
print('广播两个不同形状的张量:', z.shape)
代码执行结果:
广播两个相同形状的张量: torch.Size([2, 3, 4])
广播两个不同形状的张量: torch.Size([2, 3, 4, 5])
现在我们知道在什么情况下两个张量是可以广播的。两个张量进行广播后的结果张量的形状计算规则如下:
1)如果两个张量shape的长度不一致,那么需要在较小长度的shape前添加1,直到两个张量的形状长度相等。
2)保证两个张量形状相等之后,每个维度上的结果维度就是当前维度上较大的那个。
以张量x和y进行广播为例,x的shape为[2, 3, 1, 5],张量y的shape为[3, 4, 1]。首先张量y的形状长度较小,因此要将该张量形状补齐为[1, 3, 4, 1],再对两个张量的每一维进行比较。从第一维看,x在一维上的大小为2,y为1,因此,结果张量在第一维的大小为2。以此类推,对每一维进行比较,得到结果张量的形状为[2, 3, 4, 5]。
由于矩阵乘法函数paddle.matmul在深度学习中使用非常多,这里需要特别说明一下它的广播规则:
1)如果两个张量均为一维,则获得点积结果。
2)如果两个张量都是二维的,则获得矩阵与矩阵的乘积。
3)如果张量x是一维,y是二维,则将x的shape转换为[1, D],与y进行矩阵相乘后再删除前置尺寸。
4)如果张量x是二维,y是一维,则获得矩阵与向量的乘积。
5)如果两个张量都是N维张量(N > 2),则根据广播规则广播非矩阵维度(除最后两个维度外其余维度)。比如:如果输入x是形状为[j,1,n,m]的张量,另一个y是[k,m,p]的张量,则输出张量的形状为[j,k,n,p]。
此外,计算张量乘积时会使用到广播机制。[4]
三、数据预处理
进行实验前,我们需要先导入pandas包。
import pandas as pd
1. 读取数据集 house_tiny.csv、boston_house_prices.csv、Iris.csv
使用read_csv函数实现csv文档的读取。
house_tiny = pd.read_csv('./house_tiny.csv')
boston_house_prices = pd.read_csv('./boston_house_prices.csv')
iris = pd.read_csv('./Iris.csv')
print(house_tiny)
代码执行结果:
NumRooms Alley Price
0 NaN Pave 127500
1 2.0 NaN 106000
2 4.0 NaN 178100
3 NaN NaN 140000
2. 处理缺失值
使用get_dummies函数实现Alley的分类表示。
get_dummies函数官方文档:
pandas.get_dummies(data, prefix=None, prefix_sep=’_’, dummy_na=False, columns=None, sparse=False, drop_first=False)[source]
house_tiny = house_tiny.fillna(house_tiny.iloc[:, 0:2].mean())
house_tiny = pd.get_dummies(house_tiny, dummy_na=True).iloc[:, [0, 2, 3, 1]] # 价格移动到最后一列
print(house_tiny)
代码执行结果:
NumRooms Alley_Pave Alley_nan Price
0 3.0 1 0 127500
1 2.0 0 1 106000
2 4.0 0 1 178100
3 3.0 0 1 140000
3. 转换为张量格式
直接用前文的torch.Tensor转换即可,转换前需要先用values属性获取数据。
a = torch.Tensor(house_tiny.values)
print(a)
代码执行结果:
tensor([[3.0000e+00, 1.0000e+00, 0.0000e+00, 1.2750e+05],
[2.0000e+00, 0.0000e+00, 1.0000e+00, 1.0600e+05],
[4.0000e+00, 0.0000e+00, 1.0000e+00, 1.7810e+05],
[3.0000e+00, 0.0000e+00, 1.0000e+00, 1.4000e+05]])
四、实验总结
本次实验主要对张量和算子进行学习和应用,其中广播机制的内容…还需要再学习巩固一下。有关于收获的话…paddle包中的size属性对应在torch中是numel,在torch中size和shape的作用类似。数据预处理部分主要回忆了数据集的读取、处理,其中张量转换部分直接按照矩阵处理即可。
看来我还需要趁着周末缓缓。人真的快要寄了(悲)