基于DEAP库的python进化算法-6.遗传算法中的约束处理
文章目录
-
-
- 前言
- 一.罚函数法简介和实现思路
-
- 1.罚函数法的基本思想
- 2.实现思路
- 二.各类罚函数详解与代码实现
-
- 1.死亡惩罚
- 2.静态惩罚(Static Penalty)
- 3.动态惩罚(Dynamic Penalty)
- 4.退火惩罚(Annealing Penalty)
- 5.自适应惩罚(Adaptive Penalty)
- 三.简单测试
-
- 1.施加死亡惩罚
- 2.施加静态惩罚
- 3.施加动态惩罚
- 4.小结
- 四.实际问题测试
-
- 1.个体描述
- 2.代码实现
-
- 死亡惩罚
- 静态惩罚
-
前言
这一节我们想要探讨如何在遗传算法中处理约束,这部分内容主要是对Coello Coello大神的经典文章《Theoretical and numerical constraint-handling techniques used with evolutionary algorithms: a survey of the state of the art》的再加工以及代码实现。想要更加深入了解的同学,强烈推荐阅读一下这篇文章。
一.罚函数法简介和实现思路
1.罚函数法的基本思想
用遗传算法求解约束优化问题时,罚函数法是最常见的一种有效手段。罚函数法的基本思想是通过在适应度函数中对违反约束的个体施加惩罚,将约束优化问题转化为求解无约束优化问题。
罚函数法在使用中面临的最大问题是如何选取合适的惩罚函数:
- 惩罚系数较大,族群会更加集中在可行域中,而不鼓励向不可行域探索。当惩罚系数过大,容易使算法收敛于局部最优;
- 惩罚系数较小,族群会更积极在不可行域中进行大量探索,一定程度上能帮助寻找全局最优,但也有浪费算力的风险。当惩罚系数过小,算法可能会收敛于不可行解。
在通常的罚函数设计中,有三种惩罚的思路:
-
无论违反约束的程度如何,只要违反了约束,就施加以同样力度的惩罚
-
根据违反约束程度的不同加以惩罚;
-
根据不可行解“修复”的难度或者距离可行域的距离施加惩罚。
2.实现思路
罚函数法主要有以下几种:
- 死亡惩罚(Death Penalty)
死亡惩罚简单粗暴,对于非可行解,直接将其适应度函数调整到极容易被淘汰的大小(常用归零),使其“死亡”。 - 静态惩罚(Static Penalty)
顾名思义,在静态惩罚中,通过在适应度函数中整合惩罚项,降低违反约束的个体的适应度,在计算中惩罚系数为常数,不会随着算法迭代变化。 - 动态惩罚(Dynamic Penalty)
在动态惩罚中,惩罚系数会随着代数变化。通常为保证收敛性,惩罚系数会随着迭代进行而逐渐增大。 - 退火惩罚(Annealing Penalty)
结合模拟退火的思想,惩罚系数在一定代数内保持稳定,呈阶梯式调整。 - 自适应惩罚(Adaptive Penalty)
自适应惩罚的思想是从遗传算法迭代的过程中获得反馈,由得到的解质量来判定是要加大还是较小惩罚系数。
二.各类罚函数详解与代码实现
1.死亡惩罚
死亡惩罚就是对所有违反约束的解个体分配一个极差的适应度,例如归零或者在最小化问题中设为一个很大的值。通过这样操作,在后续的选择和变异操作中,不可行解就会被筛选掉。
死亡惩罚是在进化算法中非常流行的惩罚策略,其优点在于实施简单,但是缺点也不少:首先,它只能适用于可行域占解空间比例较大的情况,如果可行域很小,那么初始生成个体很可能没有落于其中的,那么就会全部死亡,使算法陷入停滞;其次,它没有从不可行解中利用任何信息,不能为下一步的进化提供指导,也就是前人的牺牲对于后人完全没有意义。各类研究都表明死亡惩罚是一种比较弱的方法,基本所有其他惩罚方法都能在结果或搜索效率上吊锤它。
利用DEAP提供的装饰器实现死亡惩罚-代码实现
deap.tools.DeltaPenalty(feasibility, delta[, distance])
这个装饰器为无效的个体返回惩罚适应度,并为有效的个体返回原始适应度值。
惩罚的适应度由一个常数因子delta加上一个(可选的)距离惩罚组成。如果提供了距离函数,则返回的值将随着个体离开有效区域而增长
参数:
feasibility:返回任何个体的有效性状态函数
delta:为无效个体返回的常量或常量数组
distance:返回个体与给定有效点之间距离的函数。距离函数也可以返回一个长度序列,等于目标的数量,
以不同的方式影响多目标适配(可选,默认为0)
return 返回求值函数的装饰器
decorate(alias, decorator[, decorator[, ...]])
用指定的装饰器装饰别名,别名必须是当前工具箱中的注册函数
参数:
alias:别名
decorator:一个或多个函数装饰器。
如果提供了多个装饰器,则将按顺序应用它们,最后一个装饰器将装饰所有其他装饰器
def feasible(ind):
# 判定解是否满足约束条件
# 如果满足约束条件,返回True,否则返回False
if feasible:
return True
return False
## 用装饰器修饰评价函数
toolbox.register('evaluate', evalFit) # 不加约束的评价函数
# 假设时最小化问题,并且已知的最小值远小于1e3
toolbox.decorate('evaluate', tools.DeltaPenalty(feasible, 1e3)) # death penalty
# 这样添加装饰器之后,在feasible返回True的时候,评价函数会返回evalFit的返回值;否则会返回1e3。
2.静态惩罚(Static Penalty)
静态惩罚会将违反约束的程度作为一种考量,在加权后纳入到适应度函数当中。权重在迭代过程当中保持不变,这就是“静态”名字的由来。相比于死亡惩罚绝不允许个体踏出可行域,静态惩罚允许一定程度的由外至内的搜索,因此其搜索效果会相对较好 – 尤其考虑到很多约束优化的最优解会落在可行域边界和顶点上。

3.动态惩罚(Dynamic Penalty)
动态惩罚是对于静态惩罚的一种改进,它的思想是在迭代过程中动态改变惩罚系数,在扩大搜索范围和保证收敛性之间取得动态平衡。

4.退火惩罚(Annealing Penalty)
退火惩罚实际上也是一种动态惩罚,只是它的惩罚系数调整的方式来自于模拟退火算法,以一种类似模拟退火中的temperature schedule的方式来动态调整惩罚系数。

5.自适应惩罚(Adaptive Penalty)
自适应惩罚是对动态惩罚的一种演进,它的主要思路在于从迭代过程中取得反馈,用这个反馈来指导迭代系数的调整。

三.简单测试
用简单的函数来测试各类约束下的GA算法是否能够如预期般工作
目标函数:
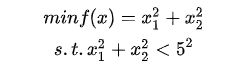
准备测试的惩罚方式有:
- 死亡惩罚
- 静态惩罚
- 动态惩罚
1.施加死亡惩罚
#!usr/bin/env python
# -*- coding:utf-8 _*-
"""
@author: liujie
@software: PyCharm
@file: 死亡惩罚.py
@time: 2020/11/26 20:46
"""
import random
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import bernoulli
from deap import creator,tools,base
# random.seed(42)
# 定义问题
creator.create('FitnessMin',base.Fitness,weights=(-1.0,)) # 单变量优化最小值
creator.create('Individual',list,fitness = creator.FitnessMin)
# 个体编码
def uniform(low,up):
# 均匀分布生成个体
return [random.uniform(low[0],up[0]),random.uniform(low[1],up[1])]
gen_size = 2
# 两个变量下界
low = [-10] * gen_size
# 两个变量上界
up = [10] * gen_size
# 生成个体
toolbox = base.Toolbox()
toolbox.register('Attr_float',uniform,low,up)
toolbox.register('Individual',tools.initIterate,creator.Individual,toolbox.Attr_float)
toolbox.register('Population',tools.initRepeat,list,toolbox.Individual)
# 生成初始种群
pop_size = 100
pop = toolbox.Population(n=pop_size)
# print(pop)
# 死亡惩罚实现约束
# 评价函数
def eval(ind):
return (ind[0]**2 + ind[1]**2),
# 死亡惩罚
def feasible(ind):
# 判定解是否可行
if (ind[0]**2 + ind[1]**2) < 25:
return True
return False
toolbox.register('evaluate',eval)
toolbox.decorate('evaluate',tools.DeltaPenality(feasible,100))
# 在feasible函数满足True时,评价函数会返回eval值,否则返回100
# 注册进化过程中需要的工具:配种选择、交叉、变异
toolbox.register('select',tools.selTournament,tournsize=2) # 锦标赛选择缺k
toolbox.register('mate',tools.cxSimulatedBinaryBounded,eta=20,low=low,up=up) # 执行模拟二值交叉多了输入
toolbox.register('mutate',tools.mutPolynomialBounded,eta=20,low=low,up=up,indpb=0.2)
# 用数据记录算法迭代过程
stats = tools.Statistics(key= lambda ind : ind.fitness.values)
stats.register('avg',np.mean)
stats.register('std',np.std)
stats.register('min',np.min)
stats.register('max',np.max)
# 创建日志对象
logbook = tools.Logbook()
# 进化迭代,不妨设置如下参数
N_Gen = 50
CXPB = 0.8
MUTPB = 0.2
# 评价初代种群
fitnesses = map(toolbox.evaluate,pop)
for ind,fit in zip(pop,fitnesses):
ind.fitness.values = fit
record = stats.compile(pop)
logbook.record(gen=0,**record)
# 族群迭代-从第二代开始
for gen in range(1,N_Gen+1):
# 配种选择
selectTour = toolbox.select(pop,pop_size*2)
# 复制个体,供交叉使用
selectInd = list(map(toolbox.clone,selectTour))
# print(selectInd)
# 对选出的个体两两进行交叉,对于被改变的个体,删除其适应度
for child1,child2 in zip(selectInd[::2],selectInd[1::2]):
if random.random() < CXPB:
toolbox.mate(child1,child2)
del child1.fitness.values
del child2.fitness.values
# 变异
for mutate in selectInd:
if random.random() < MUTPB:
toolbox.mutate(mutate)
del mutate.fitness.values
# 对于被改变的个体,重新计算其适应度
invalid_ind = [ind for ind in selectInd if not ind.fitness.valid]
fitnesses = map(toolbox.evaluate,invalid_ind)
for ind,fit in zip(invalid_ind,fitnesses):
ind.fitness.values = fit
# 精英育种-环境选择
combinedPop = pop + selectInd
pop = tools.selBest(combinedPop,pop_size)
# 记录数据-将stats注册功能应用于pop,并作为字典返回
record = stats.compile(pop)
logbook.record(gen = gen,**record)
# 输出计算过程
logbook.header = 'gen','avg','std','min','max'
print(logbook)
# 输出最优解
bestInd =tools.selBest(pop,1)[0]
bestFit =bestInd.fitness.values[0]
print('当前最优解为:',str(bestInd))
print('对应的函数最小值为:',str(bestFit))
# 打印变化值
import matplotlib.pyplot as plt
# 用select方法从logbook提取迭代次数、最大值、均值
gen = logbook.select('gen')
fitness_min = logbook.select('min')
fitness_avg = logbook.select('avg')
fig = plt.figure()
fig.add_subplot()
plt.plot(gen,fitness_avg,'r-',label='fitness_avg')
plt.plot(gen,fitness_min,'b-',label='fitness_min')
plt.legend(loc='best')
plt.xlabel('gen')
plt.ylabel('fitness')
plt.tight_layout()
plt.show()
运行结果
gen avg std min max
0 85.3762 32.3885 5.39498 100
1 34.5869 37.0758 0.875777 100
2 6.98103 3.17577 0.413046 11.6163
3 2.44319 1.26582 0.185718 4.05851
4 0.602292 0.203323 0.168649 0.875777
5 0.290384 0.105916 0.0124754 0.413046
6 0.155608 0.052468 0.0107238 0.185718
7 0.0851795 0.057145 0.00840087 0.168649
8 0.0151213 0.00562544 0.00492679 0.0302032
9 0.00993487 0.00161344 0.0049257 0.0109324
10 0.00701735 0.00175296 0.00464194 0.00975164
11 0.00494503 7.77257e-05 0.0046419 0.00514399
12 0.00487061 9.58943e-05 0.00462247 0.00492554
13 0.00469287 7.70745e-05 0.00461571 0.00485848
14 0.00459995 0.000359214 0.0010266 0.0046419
15 0.00444215 0.000779656 0.00102653 0.00463406
16 0.00385545 0.00145845 0.000881858 0.00461572
17 0.00101016 0.000105125 0.000132828 0.00116749
18 0.000913377 0.000164413 0.000132827 0.000989294
19 0.00075215 0.000279111 0.00012942 0.000886589
20 0.000300576 0.000304211 9.24263e-05 0.000864569
21 0.000126897 8.93438e-06 9.23114e-05 0.000132189
22 0.000111133 1.38482e-05 2.83213e-05 0.000128747
23 9.54871e-05 1.1774e-05 2.83213e-05 0.000107235
24 8.7466e-05 1.51493e-05 2.40618e-05 9.2114e-05
25 7.0977e-05 2.80402e-05 2.12228e-05 9.04144e-05
26 2.68166e-05 2.50403e-06 1.51608e-05 2.86062e-05
27 2.29284e-05 2.73313e-06 1.50084e-05 2.59075e-05
28 1.89295e-05 2.58017e-06 1.49824e-05 2.12228e-05
29 1.511e-05 7.23405e-08 1.49092e-05 1.5183e-05
30 1.49754e-05 5.03042e-08 1.47897e-05 1.50466e-05
31 1.49039e-05 3.8587e-08 1.47772e-05 1.4934e-05
32 1.48497e-05 5.33258e-08 1.47764e-05 1.49075e-05
33 1.47861e-05 5.18862e-09 1.47686e-05 1.47921e-05
34 1.47775e-05 3.40141e-09 1.4768e-05 1.47851e-05
35 1.47738e-05 2.83726e-09 1.47678e-05 1.47769e-05
36 1.47694e-05 1.78033e-09 1.47672e-05 1.47726e-05
37 1.47679e-05 2.32567e-10 1.47672e-05 1.47681e-05
38 1.47675e-05 2.31802e-10 1.47671e-05 1.47678e-05
39 1.47672e-05 3.60913e-11 1.47671e-05 1.47672e-05
40 1.47671e-05 4.38304e-11 1.47671e-05 1.47672e-05
41 1.47671e-05 1.22742e-11 1.47671e-05 1.47671e-05
42 1.47671e-05 8.63164e-12 1.4767e-05 1.47671e-05
43 1.47671e-05 8.70228e-12 1.4767e-05 1.47671e-05
44 1.4767e-05 5.57906e-12 1.4767e-05 1.4767e-05
45 1.4767e-05 1.45335e-12 1.4767e-05 1.4767e-05
46 1.4767e-05 3.89769e-13 1.4767e-05 1.4767e-05
47 1.4767e-05 8.65246e-14 1.4767e-05 1.4767e-05
48 1.47449e-05 2.20077e-07 1.25552e-05 1.4767e-05
49 1.46343e-05 5.25287e-07 1.25552e-05 1.4767e-05
50 1.40995e-05 1.01579e-06 1.24467e-05 1.4767e-05
当前最优解为: [0.003506251190284561, 0.0003909908406204978]
对应的函数最小值为: 1.2446671246821023e-05
可视化
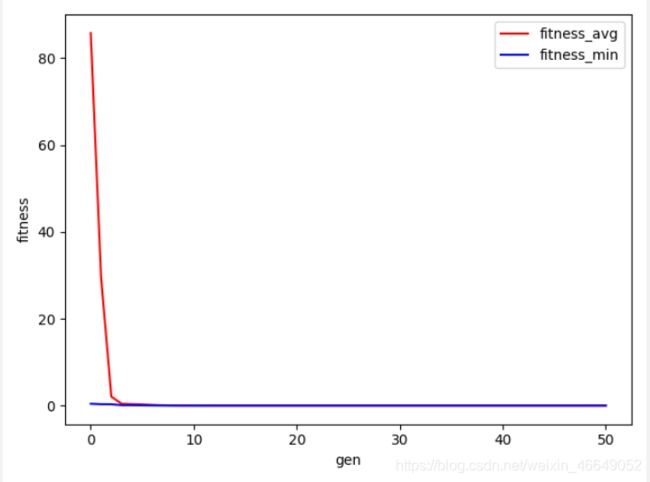
由上可知,只要个体不落在可行域内,就使其适应度为100,这个值远大于其他可行解的适应度,因此,我们可以期待这种个体很快就会在迭代中被淘汰灭绝,从而留下的解都能落在可行域内。
2.施加静态惩罚
静态惩罚就是在原先的目标函数上加上 一个静态惩罚项,实现起来比较容易:
#!usr/bin/env python
# -*- coding:utf-8 _*-
"""
@author: liujie
@software: PyCharm
@file: 死亡惩罚.py
@time: 2020/11/26 20:46
"""
import random
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import bernoulli
from deap import creator,tools,base
# random.seed(42)
# 定义问题
creator.create('FitnessMin',base.Fitness,weights=(-1.0,)) # 单变量优化最小值
creator.create('Individual',list,fitness = creator.FitnessMin)
# 基因长度取2
gen_size = 2
low = [-10] * gen_size
up = [10] * gen_size
# 个体解码-均匀分布生成个体
def uniform(low,up):
return [random.uniform(low[0],up[0]),random.uniform(low[1],up[1])]
toolbox = base.Toolbox()
toolbox.register('Attr_float',uniform,low,up) # (-10,10)
toolbox.register('Individual',tools.initIterate,creator.Individual,toolbox.Attr_float)
# 生成初始种群
pop_size = 100
toolbox.register('Population',tools.initRepeat,list,toolbox.Individual)
pop = toolbox.Population(n=pop_size)
# 评价函数+静态惩罚项
def eval(ind):
return (ind[0]**2 + ind[1]**2 + StaticPenalty(ind)),
def StaticPenalty(ind):
# 判定解是否可行
if (ind[0]**2 + ind[1]**2) < 25:
return 0
# 当解不可行时,施加静态惩罚
return np.sqrt(ind[0]**2 + ind[1]**2 - 25)
toolbox.register('evaluate',eval)
# 注册进化过程中需要的工具:配种选择、交叉、变异
toolbox.register('select',tools.selRoulette) # 锦标赛选择缺k
toolbox.register('mate',tools.cxSimulatedBinaryBounded,eta = 20,low = low,up = up)
toolbox.register('mutate',tools.mutPolynomialBounded,eta=10,low = low,up=up,indpb=0.2)
# 用数据记录算法迭代过程
stats = tools.Statistics(key= lambda ind : ind.fitness.values)
stats.register('avg',np.mean)
stats.register('std',np.std)
stats.register('min',np.min)
stats.register('max',np.max)
# 创建日志对象
logbook = tools.Logbook()
# 评价初代种群
fitnesses = map(toolbox.evaluate,pop)
for ind,fit in zip(pop,fitnesses):
ind.fitness.values = fit
record = stats.compile(pop)
logbook.record(gen=0,**record)
# 进化迭代,不妨设置如下参数
N_Gen = 100
CXPB = 0.8
MUTPB = 0.2
# 遗传算法迭代
for gen in range(1,N_Gen+1):
# 配种选择
selectTour = toolbox.select(pop,pop_size*2)
# 复制个体,供交叉使用
selectInd = list(map(toolbox.clone,selectTour))
# print(selectInd)
# 对选出的个体两两进行交叉,对于被改变的个体,删除其适应度
for child1,child2 in zip(selectInd[::2],selectInd[1::2]):
if random.random() < CXPB:
toolbox.mate(child1,child2)
del child1.fitness.values
del child2.fitness.values
# 变异
for ind in selectInd:
if random.random() < MUTPB:
toolbox.mutate(ind)
del ind.fitness.values
# 对于被改变的物体,重新计算其适应度
invalid_ind = [ind for ind in selectInd if not ind.fitness.valid]
fitnesses = map(toolbox.evaluate,invalid_ind)
for ind,fit in zip(invalid_ind,fitnesses):
ind.fitness.values = fit
# 精英育种
combinedPop = pop + selectInd
pop = tools.selBest(combinedPop,pop_size)
# 记录数据-将stats注册功能应用于pop,并作为字典返回
record = stats.compile(pop)
logbook.record(gen = gen,**record)
# 输出计算过程
logbook.header = 'gen','avg','std','min','max'
print(logbook)
# 输出最优解
bestInd = tools.selBest(pop,1)[0]
bestFit = bestInd.fitness.values[0]
print('当前最优解:',str(bestInd))
print('对应的函数最小值为:'+str(bestFit))
# 打印变化值
import matplotlib.pyplot as plt
# 用select方法从logbook提取迭代次数、最大值、均值
gen = logbook.select('gen')
fitness_min = logbook.select('min')
fitness_avg = logbook.select('avg')
fig = plt.figure()
fig.add_subplot()
plt.plot(gen,fitness_avg,'r-',label='fitness_avg')
plt.plot(gen,fitness_min,'b-',label='fitness_min')
plt.legend(loc='best')
plt.xlabel('gen')
plt.ylabel('fitness')
plt.show()
运行结果
gen avg std min max
0 69.335 44.0601 0.118268 180.778
1 38.4895 19.3427 0.118268 64.9018
2 22.0837 11.5997 0.118268 39.0486
3 13.4385 6.447 0.118268 21.9065
4 7.97693 3.84648 0.118268 13.36
5 5.25142 2.36694 0.118268 8.91135
6 3.0946 1.16566 0.118268 4.61471
7 1.95966 0.73068 0.118268 3.19515
8 1.37402 0.408289 0.030205 1.81653
9 0.967739 0.320939 0.030205 1.34296
10 0.697352 0.212141 0.030205 0.914241
11 0.512401 0.167702 0.0122097 0.632152
12 0.395799 0.157598 0.0122097 0.583019
13 0.263748 0.108517 0.000532408 0.405275
14 0.160498 0.0839787 0.000330906 0.262199
15 0.11545 0.0682897 0.000330906 0.191441
16 0.0650582 0.0463801 0.000330906 0.119823
17 0.0314148 0.0214037 0.000330906 0.0729015
18 0.0175486 0.00992066 0.000330906 0.0294054
19 0.0102171 0.00596432 0.000330906 0.0195886
20 0.00579075 0.00260294 0.000330906 0.00990464
21 0.00398794 0.00171938 0.000330906 0.0057771
22 0.00291931 0.00147234 0.000330906 0.00473133
23 0.00175682 0.00096448 0.000330906 0.00323461
24 0.000951754 0.000333543 0.000119894 0.00151962
25 0.000588797 0.000182533 7.19251e-05 0.000874826
26 0.000432798 0.000110782 7.19251e-05 0.000528845
27 0.000347021 8.55383e-05 7.19251e-05 0.000446704
28 0.00027675 6.16591e-05 7.19251e-05 0.000346742
29 0.000219269 2.92719e-05 7.19251e-05 0.000245368
30 0.000194593 2.98235e-05 7.19251e-05 0.000219386
31 0.000175324 3.19589e-05 7.19251e-05 0.000198405
32 0.000157782 3.23906e-05 7.19251e-05 0.000183222
33 0.000129324 2.90981e-05 6.90526e-05 0.000161047
34 0.00010463 2.55857e-05 5.98335e-05 0.000133407
35 7.5984e-05 7.70982e-06 5.97185e-05 9.63063e-05
36 6.87865e-05 4.13999e-06 5.90387e-05 7.41564e-05
37 6.48259e-05 3.46238e-06 5.671e-05 6.97849e-05
38 6.1742e-05 1.92897e-06 5.65211e-05 6.34584e-05
39 5.95981e-05 1.07885e-06 5.63393e-05 6.13649e-05
40 5.84794e-05 1.15407e-06 5.62782e-05 5.96736e-05
41 5.70162e-05 6.36412e-07 5.6202e-05 5.89753e-05
42 5.64843e-05 1.96093e-07 5.578e-05 5.67453e-05
43 5.62558e-05 1.17824e-07 5.578e-05 5.63451e-05
44 5.61355e-05 1.56324e-07 5.578e-05 5.62782e-05
45 5.59544e-05 1.5793e-07 5.56026e-05 5.61023e-05
46 5.57566e-05 5.70612e-08 5.56026e-05 5.57838e-05
47 5.57161e-05 7.72078e-08 5.56025e-05 5.57787e-05
48 5.56178e-05 3.32351e-08 5.55979e-05 5.57604e-05
49 5.5603e-05 1.78153e-09 5.55979e-05 5.56061e-05
50 5.56014e-05 1.76748e-09 5.55936e-05 5.56026e-05
51 5.55989e-05 1.93015e-09 5.55922e-05 5.56018e-05
52 5.55964e-05 2.23271e-09 5.55882e-05 5.55979e-05
53 5.55935e-05 2.63285e-09 5.55882e-05 5.55968e-05
54 5.55905e-05 1.78532e-09 5.5588e-05 5.55932e-05
55 5.55886e-05 3.15813e-10 5.55878e-05 5.5589e-05
56 5.55883e-05 1.90225e-10 5.55878e-05 5.55886e-05
57 5.55881e-05 1.04712e-10 5.55878e-05 5.55882e-05
58 5.55879e-05 8.25875e-11 5.55877e-05 5.5588e-05
59 5.55878e-05 6.40735e-11 5.55877e-05 5.55879e-05
60 5.55878e-05 2.44583e-11 5.55877e-05 5.55878e-05
61 5.55877e-05 1.86767e-11 5.55877e-05 5.55878e-05
62 5.55877e-05 8.22428e-12 5.55877e-05 5.55877e-05
63 5.55877e-05 2.38792e-12 5.55877e-05 5.55877e-05
64 5.55877e-05 9.84111e-13 5.55877e-05 5.55877e-05
65 5.55877e-05 6.82792e-13 5.55877e-05 5.55877e-05
66 5.55877e-05 9.56089e-13 5.55877e-05 5.55877e-05
67 5.55877e-05 9.4997e-13 5.55877e-05 5.55877e-05
68 5.55877e-05 3.2468e-13 5.55877e-05 5.55877e-05
69 5.55877e-05 3.0299e-13 5.55877e-05 5.55877e-05
70 5.55877e-05 1.87329e-13 5.55877e-05 5.55877e-05
71 5.55877e-05 1.67337e-13 5.55877e-05 5.55877e-05
72 5.55877e-05 4.11938e-14 5.55877e-05 5.55877e-05
73 5.55877e-05 3.34119e-14 5.55877e-05 5.55877e-05
74 5.55877e-05 1.20333e-14 5.55877e-05 5.55877e-05
75 5.55877e-05 8.77213e-15 5.55877e-05 5.55877e-05
76 5.55877e-05 4.17314e-15 5.55877e-05 5.55877e-05
77 5.55877e-05 4.5551e-15 5.55877e-05 5.55877e-05
78 5.55877e-05 4.88656e-15 5.55877e-05 5.55877e-05
79 5.55877e-05 3.60554e-15 5.55877e-05 5.55877e-05
80 5.55877e-05 5.0191e-15 5.55877e-05 5.55877e-05
81 5.55877e-05 6.33363e-15 5.55877e-05 5.55877e-05
82 5.55877e-05 4.5189e-16 5.55877e-05 5.55877e-05
83 5.55877e-05 2.7789e-16 5.55877e-05 5.55877e-05
84 5.55877e-05 1.9278e-16 5.55877e-05 5.55877e-05
85 5.55877e-05 1.61254e-16 5.55877e-05 5.55877e-05
86 5.55877e-05 1.62523e-16 5.55877e-05 5.55877e-05
87 5.55877e-05 1.21384e-16 5.55877e-05 5.55877e-05
88 5.55877e-05 2.83394e-17 5.55877e-05 5.55877e-05
89 5.55877e-05 1.42848e-17 5.55877e-05 5.55877e-05
90 5.55877e-05 9.53542e-18 5.55877e-05 5.55877e-05
91 5.55877e-05 6.42613e-18 5.55877e-05 5.55877e-05
92 5.55877e-05 1.47049e-18 5.55877e-05 5.55877e-05
93 5.55877e-05 2.32304e-18 5.55877e-05 5.55877e-05
94 5.55877e-05 2.8946e-18 5.55877e-05 5.55877e-05
95 5.55877e-05 5.23914e-19 5.55877e-05 5.55877e-05
96 5.55877e-05 2.63053e-19 5.55877e-05 5.55877e-05
97 5.55877e-05 2.03288e-20 5.55877e-05 5.55877e-05
98 5.55877e-05 2.03288e-20 5.55877e-05 5.55877e-05
99 5.55877e-05 2.03288e-20 5.55877e-05 5.55877e-05
100 5.55877e-05 2.03288e-20 5.55877e-05 5.55877e-05
当前最优解: [0.007453508849359465, -0.00018141169431430863]
对应的函数最小值为:5.558770437031385e-05
3.施加动态惩罚
动态惩罚需要记录个体的迭代次数,为了简单实现,我们生成个体的时候就直接赋予一个gen属性以记录当时迭代步数:
#!usr/bin/env python
# -*- coding:utf-8 _*-
"""
@author: liujie
@software: PyCharm
@file: 动态惩罚.py
@time: 2020/11/27 12:46
"""
import random
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import bernoulli
from deap import creator,tools,base
# random.seed(42)
# 定义问题
creator.create('FitnessMin',base.Fitness,weights=(-1.0,)) # 单变量优化最小值
creator.create('DynamicIndividual',list,fitness = creator.FitnessMin,gen = None)
# 基因长度取2
gen_size = 2
low = [-10] * gen_size
up = [10] * gen_size
# 个体解码-均匀分布生成个体
def uniform(low,up):
return [random.uniform(low[0],up[0]),random.uniform(low[1],up[1])]
toolbox = base.Toolbox()
toolbox.register('Attr_float',uniform,low,up) # (-10,10)
toolbox.register('DynamicIndividual',tools.initIterate,creator.DynamicIndividual,toolbox.Attr_float)
# 生成初始种群
pop_size = 100
toolbox.register('Population',tools.initRepeat,list,toolbox.DynamicIndividual)
pop = toolbox.Population(n=pop_size)
# 动态惩罚实现约束
# 评价函数+动态惩罚项
def evalDynamic(ind):
return (ind[0]**2 + ind[1]**2 + DynamicPenalty(ind)),
def DynamicPenalty(ind):
# 判定解是否可行
if ind.gen:
# print(ind.gen)
# 求解惩罚函数,用默认参数 C = 0.5, alpha = 2, beta = 2
cons = ind[0] * ind[0] + ind[1] * ind[1] - 5 * 5
cons = np.where(cons > 0, cons, 0)
SVC = np.sum(np.square(cons))
return (0.5 * ind.gen) * (0.5 * ind.gen) * SVC
# 第0代时,没有惩罚
else:
return 0
toolbox.register('evaluate',evalDynamic)
# 注册进化过程中需要的工具:配种选择、交叉、变异
toolbox.register('select',tools.selRoulette) # 锦标赛选择缺k
toolbox.register('mate',tools.cxSimulatedBinaryBounded,eta = 20,low = low,up = up)
toolbox.register('mutate',tools.mutPolynomialBounded,eta=10,low = low,up=up,indpb=0.2)
# 用数据记录算法迭代过程
stats = tools.Statistics(key= lambda ind : ind.fitness.values)
stats.register('avg',np.mean)
stats.register('std',np.std)
stats.register('min',np.min)
stats.register('max',np.max)
# 创建日志对象
logbook = tools.Logbook()
# 评价初代种群
fitnesses = map(toolbox.evaluate,pop)
for ind,fit in zip(pop,fitnesses):
ind.fitness.values = fit
record = stats.compile(pop)
logbook.record(gen=0,**record)
# 进化迭代,不妨设置如下参数
N_Gen = 100
CXPB = 0.8
MUTPB = 0.2
# 遗传算法迭代
for gen in range(1,N_Gen+1):
# 更新个体中的gen参数,为后面计算动态惩罚用
for ind in pop:
ind.gen = gen
# 配种选择
selectTour = toolbox.select(pop,pop_size*2)
# 复制个体,供交叉使用
selectInd = list(map(toolbox.clone,selectTour))
# print(selectInd)
# 对选出的个体两两进行交叉,对于被改变的个体,删除其适应度
for child1,child2 in zip(selectInd[::2],selectInd[1::2]):
if random.random() < CXPB:
toolbox.mate(child1,child2)
del child1.fitness.values
del child2.fitness.values
# 变异
for ind in selectInd:
if random.random() < MUTPB:
toolbox.mutate(ind)
del ind.fitness.values
# 对于被改变的物体,重新计算其适应度
invalid_ind = [ind for ind in selectInd if not ind.fitness.valid]
fitnesses = map(toolbox.evaluate,invalid_ind)
for ind,fit in zip(invalid_ind,fitnesses):
ind.fitness.values = fit
# 精英育种
combinedPop = pop + selectInd
pop = tools.selBest(combinedPop,pop_size)
# 记录数据-将stats注册功能应用于pop,并作为字典返回
record = stats.compile(pop)
logbook.record(gen = gen,**record)
# 输出计算过程
logbook.header = 'gen','avg','std','min','max'
print(logbook)
# 输出最优解
bestInd = tools.selBest(pop,1)[0]
bestFit = bestInd.fitness.values[0]
print('当前最优解:',str(bestInd))
print('对应的函数最小值为:'+str(bestFit))
# 打印变化值
import matplotlib.pyplot as plt
# 用select方法从logbook提取迭代次数、最大值、均值
gen = logbook.select('gen')
fitness_min = logbook.select('min')
fitness_avg = logbook.select('avg')
fig = plt.figure()
fig.add_subplot()
plt.plot(gen,fitness_avg,'r-',label='fitness_avg')
plt.plot(gen,fitness_min,'b-',label='fitness_min')
plt.legend(loc='best')
plt.xlabel('gen')
plt.ylabel('fitness')
plt.show()
运行结果
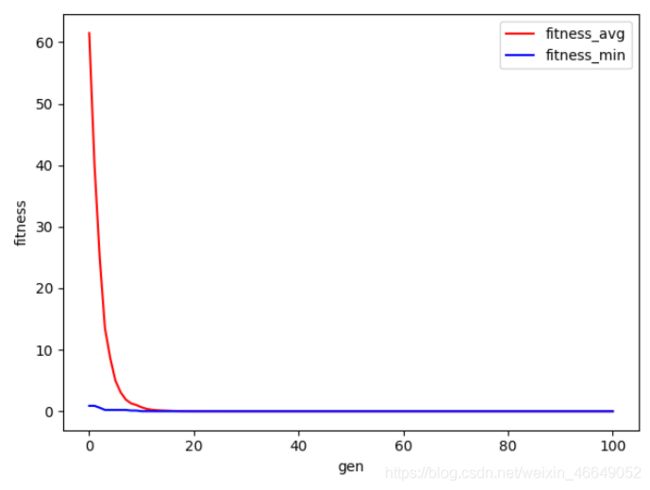
gen avg std min max
0 61.4943 38.7817 0.881897 162.213
1 40.1342 20.7213 0.881897 73.8668
2 25.001 10.7355 0.57536 40.7019
3 13.5064 5.62591 0.211234 21.4994
4 8.6753 3.6985 0.211234 13.6767
5 4.9856 2.01538 0.211234 7.96541
6 3.06883 1.40504 0.211234 5.0798
7 1.88329 0.707604 0.211234 2.90441
8 1.27634 0.485427 0.116052 1.75309
9 1.01099 0.40625 0.107841 1.43434
10 0.642157 0.343268 0.00991432 1.1205
11 0.380156 0.17224 0.00991432 0.584623
12 0.236136 0.0926998 0.00456964 0.340299
13 0.160097 0.0845773 0.000626169 0.252349
14 0.115855 0.0665398 0.000626169 0.189957
15 0.0857403 0.0541806 0.000626169 0.144469
16 0.0467774 0.0314094 0.000626169 0.111023
17 0.0245054 0.0151054 0.000626169 0.0481225
18 0.0140231 0.00888138 0.000626169 0.0291153
19 0.00659565 0.00340061 1.43492e-06 0.0115689
20 0.00422798 0.00171975 1.43492e-06 0.00659726
21 0.00290527 0.00092396 1.43492e-06 0.00396387
22 0.00228661 0.000789963 1.43492e-06 0.00304241
23 0.00168798 0.0005634 1.43492e-06 0.00246746
24 0.00129954 0.000410606 1.43492e-06 0.00182337
25 0.000940636 0.000244947 1.43492e-06 0.00125262
26 0.000713707 0.000163646 1.43492e-06 0.000919848
27 0.000592478 0.000118863 1.43492e-06 0.000657115
28 0.000568431 0.000115116 1.43492e-06 0.000621172
29 0.00054423 0.000113334 1.43492e-06 0.000586776
30 0.0005145 0.000113852 1.43492e-06 0.000579166
31 0.000460871 0.000103018 1.43492e-06 0.000565632
32 0.00040624 8.61492e-05 1.43492e-06 0.000432537
33 0.000398869 9.3769e-05 1.43492e-06 0.00042414
34 0.000396189 9.31415e-05 1.43492e-06 0.000423343
35 0.000387488 9.8278e-05 1.43492e-06 0.000420189
36 0.000376858 0.000108533 1.43492e-06 0.000412165
37 0.000372116 0.000113804 1.43492e-06 0.000410427
38 0.000364042 0.000123859 1.43492e-06 0.000409767
39 0.000352594 0.000136142 1.43492e-06 0.000409746
40 0.00034888 0.000139541 1.43492e-06 0.000409741
41 0.000348874 0.000139538 1.43492e-06 0.000409734
42 0.000337744 0.000148722 1.43492e-06 0.000409724
43 0.000329973 0.000154047 1.43492e-06 0.000409724
44 0.000310448 0.000166159 1.43492e-06 0.000409716
45 0.000294001 0.000173292 1.43492e-06 0.000409715
46 0.000276 0.000173039 1.43492e-06 0.000409714
47 0.000251512 0.00016655 1.43492e-06 0.000379026
48 0.000226609 0.000167707 1.43492e-06 0.000378644
49 0.000191797 0.000158302 1.43492e-06 0.000351986
50 0.000122865 0.000141527 1.43492e-06 0.000339433
51 2.98877e-05 1.23799e-05 1.21295e-06 4.11266e-05
52 2.16437e-05 1.14033e-05 1.21295e-06 3.58769e-05
53 1.11603e-05 3.97411e-06 1.21295e-06 1.90721e-05
54 8.51981e-06 2.68158e-06 1.16999e-06 1.06777e-05
55 6.49201e-06 2.02908e-06 1.16999e-06 1.00827e-05
56 5.46303e-06 1.47026e-06 1.16999e-06 6.38918e-06
57 4.6226e-06 1.45266e-06 1.16999e-06 6.07204e-06
58 3.46689e-06 8.18202e-07 1.16999e-06 5.461e-06
59 3.03891e-06 7.99243e-07 1.16999e-06 3.69304e-06
60 2.28521e-06 5.81135e-07 1.16942e-06 3.608e-06
61 1.97037e-06 2.19665e-07 1.16942e-06 2.14217e-06
62 1.76233e-06 2.39217e-07 1.16942e-06 2.02955e-06
63 1.57901e-06 2.49628e-07 1.00886e-06 1.76651e-06
64 1.30779e-06 2.00498e-07 6.94122e-07 1.74348e-06
65 1.13688e-06 8.07853e-08 6.94122e-07 1.17093e-06
66 1.10115e-06 8.49846e-08 6.94122e-07 1.15181e-06
67 1.02515e-06 1.05732e-07 6.94122e-07 1.11074e-06
68 9.23371e-07 9.29678e-08 6.69365e-07 1.06108e-06
69 8.17112e-07 9.97261e-08 4.21883e-07 9.13673e-07
70 7.01149e-07 8.43517e-08 4.21883e-07 8.13339e-07
71 6.33242e-07 9.57715e-08 3.99499e-07 7.01383e-07
72 5.40274e-07 9.99523e-08 3.38938e-07 6.69365e-07
73 4.25758e-07 3.66205e-08 2.46433e-07 4.68675e-07
74 3.95647e-07 3.22616e-08 2.46433e-07 4.2296e-07
75 3.67954e-07 2.90219e-08 2.31127e-07 3.97988e-07
76 3.40964e-07 2.30273e-08 2.31127e-07 3.68479e-07
77 3.17165e-07 2.25429e-08 2.31127e-07 3.38938e-07
78 2.9311e-07 2.6323e-08 2.11702e-07 3.17454e-07
79 2.63773e-07 2.4633e-08 1.29901e-07 2.92496e-07
80 2.37357e-07 2.04238e-08 1.29897e-07 2.60749e-07
81 2.15744e-07 2.51745e-08 1.2807e-07 2.33013e-07
82 1.96097e-07 2.49518e-08 1.23246e-07 2.12066e-07
83 1.79551e-07 2.35438e-08 1.23246e-07 2.01225e-07
84 1.5479e-07 2.2493e-08 1.19804e-07 1.8027e-07
85 1.2685e-07 5.79031e-09 9.9354e-08 1.353e-07
86 1.20981e-07 7.39381e-09 9.9354e-08 1.26358e-07
87 1.1292e-07 6.71363e-09 9.79025e-08 1.19879e-07
88 1.065e-07 5.08639e-09 9.79025e-08 1.11304e-07
89 1.00655e-07 1.92345e-09 9.75121e-08 1.03352e-07
90 9.87124e-08 6.68171e-10 9.74954e-08 9.94198e-08
91 9.78733e-08 2.3268e-10 9.74375e-08 9.82987e-08
92 9.76244e-08 1.12812e-10 9.73376e-08 9.77758e-08
93 9.74737e-08 6.32871e-11 9.7322e-08 9.75345e-08
94 9.7399e-08 5.63678e-11 9.73058e-08 9.74995e-08
95 9.73426e-08 1.22904e-11 9.7303e-08 9.73561e-08
96 9.73304e-08 1.22276e-11 9.7293e-08 9.73392e-08
97 9.73155e-08 1.35709e-11 9.72862e-08 9.73364e-08
98 9.73005e-08 5.69146e-12 9.72862e-08 9.73045e-08
99 9.72906e-08 2.51325e-12 9.72859e-08 9.72935e-08
100 9.72875e-08 1.05193e-12 9.7285e-08 9.72892e-08
当前最优解: [-4.0296662398844107e-07, 0.00031190510835562457]
对应的函数最小值为:9.728495900043396e-08
4.小结
- 三种惩罚方式都能够实现约束的施加,上述问题,到前10代就将所有个体压入可行域;
- 从上面可以看出,动态惩罚的力度与静态惩罚的力度似乎差不多,这可能是因为迭代步数还比较少的时候个体就已经完全进入可行域;动态惩罚随着迭代步数的增长惩罚力度加大的特性还没有完全能够展现。
四.实际问题测试
1.个体描述
2.代码实现
死亡惩罚
#!usr/bin/env python
# -*- coding:utf-8 _*-
"""
@author: liujie
@software: PyCharm
@file: 实际问题-死亡惩罚.py
@time: 2020/11/27 22:21
"""
'''
这个问题有5个变量,有6个非线性不等式约束和10个边界条件
'''
import numpy as np
import random
import matplotlib.pyplot as plt
from deap import creator,tools,base,algorithms
# 定义问题
creator.create('FitnessMin',base.Fitness,weights=(-1.0,))
creator.create('Individual',list,fitness=creator.FitnessMin)
# 个体编码-5个实数
# 变量下界
lb = [78,33,27,27,27]
# 变量上界
up = [102,45,45,45,45]
def uniform(lb,up):
return [random.uniform(a,b) for a,b in zip(lb,up)]
# 生成个体
toolbox = base.Toolbox()
toolbox.register('Attr_float',uniform,lb,up)
toolbox.register('Individual',tools.initIterate,creator.Individual,toolbox.Attr_float)
# 生成种群
pop_size = 100
toolbox.register('Population',tools.initRepeat,list,toolbox.Individual)
pop = toolbox.Population(n = pop_size)
# 评价函数
def himmelblauFun(ind):
return (5.3578547*ind[2]*ind[2]+0.8356891*ind[0]*ind[4]+37.293239*ind[0]-40792.141),
# 施加约束
def feasible(ind):
# 判定解是否可行
g1 = 85.334407+0.0056858*ind[1]*ind[4]+0.00026*ind[0]*ind[3]-0.0022053*ind[2]*ind[4]
g2 = 80.51249+0.0071317*ind[1]*ind[4]+0.0029955*ind[0]*ind[1]+0.0021813*ind[2]*ind[2]
g3 = 9.300961+0.0047026*ind[2]*ind[4]+0.0012547*ind[0]*ind[2]+0.0019085*ind[2]*ind[3]
cond1 = (g1 >= 0) and (g1 <= 92)
cond2 = (g2 >= 90) and (g2 <= 110)
cond3 = (g3 >= 20) and (g3 <= 25)
if cond1 and cond2 and cond3:
return True
return False
# 注册评价函数
toolbox.register('evaluate', himmelblauFun)
toolbox.decorate('evaluate', tools.DeltaPenalty(feasible, 1e3)) # death penalty
# 注册进化过程中需要的工具:配种选择,交叉,变异
toolbox.register('select',tools.selTournament,tournsize=2) # 锦标赛
toolbox.register('mate',tools.cxSimulatedBinaryBounded,eta=20,low = lb,up = up)
toolbox.register('mutate',tools.mutPolynomialBounded,eta=20,low=lb,up=up,indpb=0.2)
# 创建统计对象
# 用数据记录算法迭代过程
stats = tools.Statistics(key= lambda ind : ind.fitness.values)
stats.register('avg',np.mean)
stats.register('std',np.std)
stats.register('min',np.min)
stats.register('max',np.max)
# 创建日志对象
logbook = tools.Logbook()
# 进化迭代,不妨设置如下参数
N_Gen = 50
CXPB = 0.8
MUTPB = 0.2
# 评价初代个体
fitnesses = map(toolbox.evaluate,pop)
for ind,fit in zip(pop,fitnesses):
ind.fitness.values = fit
record = stats.compile(pop)
logbook.record(gen=0,**record)
# 遗传算法迭代
for gen in range(1,N_Gen+1):
# 配种选择
selectTour = toolbox.select(pop,pop_size)
# 复制个体,供交叉使用
selectInd = list(map(toolbox.clone,selectTour))
# print(selectInd)
# 对选出的个体两两进行交叉,对于被改变的个体,删除其适应度
for child1,child2 in zip(selectInd[::2],selectInd[1::2]):
if random.random() < CXPB:
toolbox.mate(child1,child2)
del child1.fitness.values
del child2.fitness.values
# 变异
for mutate in selectInd:
if random.random() < MUTPB:
toolbox.mutate(mutate)
del mutate.fitness.values
# 对于被改变的个体,重新计算其适应度
invalid_ind = [ind for ind in selectInd if not ind.fitness.valid]
fitnesses = map(toolbox.evaluate,invalid_ind)
for ind,fit in zip(invalid_ind,fitnesses):
ind.fitness.values = fit
# 精英育种-环境选择
combinedPop = pop + selectTour
pop = tools.selBest(combinedPop,pop_size)
# 记录数据-将stats注册功能应用于pop,并作为字典返回
record = stats.compile(pop)
logbook.record(gen = gen,**record)
# 输出计算过程
logbook.header = 'gen','avg','std','min','max'
print(logbook)
# 输出最优解
bestInd =tools.selBest(pop,1)[0]
bestFit =bestInd.fitness.values[0]
print('当前最优解为:',str(bestInd))
print('对应的函数最小值为:',str(bestFit))
# 打印变化值
import matplotlib.pyplot as plt
# 用select方法从logbook提取迭代次数、最大值、均值
gen = logbook.select('gen')
fitness_min = logbook.select('min')
fitness_avg = logbook.select('avg')
fig = plt.figure()
fig.add_subplot()
plt.plot(gen,fitness_avg,'r-',label='fitness_avg')
plt.plot(gen,fitness_min,'b-',label='fitness_min')
plt.legend(loc='best')
plt.xlabel('gen')
plt.ylabel('fitness')
plt.tight_layout()
plt.show()
运行结果
gen avg std min max
0 47.6898 22.2587 27.0459 101.475
1 46.8968 21.5867 27.0459 100.848
2 47.0337 22.0494 27.9618 100.848
3 46.0531 21.9387 29.6829 100.808
4 45.9328 19.0679 29.6829 84.2323
5 45.3346 18.6757 29.6829 84.2323
6 44.8679 18.4201 29.6829 80.6687
7 44.8679 18.4201 29.6829 80.6687
8 44.8679 18.4201 29.6829 80.6687
9 44.8679 18.4201 29.6829 80.6687
10 44.8679 18.4201 29.6829 80.6687
11 44.8679 18.4201 29.6829 80.6687
12 44.8679 18.4201 29.6829 80.6687
13 44.8679 18.4201 29.6829 80.6687
14 44.8679 18.4201 29.6829 80.6687
15 44.8679 18.4201 29.6829 80.6687
16 44.8679 18.4201 29.6829 80.6687
17 44.8679 18.4201 29.6829 80.6687
18 44.8679 18.4201 29.6829 80.6687
19 44.8679 18.4201 29.6829 80.6687
20 44.8679 18.4201 29.6829 80.6687
21 44.8679 18.4201 29.6829 80.6687
22 44.8679 18.4201 29.6829 80.6687
23 44.8679 18.4201 29.6829 80.6687
24 44.8679 18.4201 29.6829 80.6687
25 44.8679 18.4201 29.6829 80.6687
26 44.8679 18.4201 29.6829 80.6687
27 44.8679 18.4201 29.6829 80.6687
28 44.8679 18.4201 29.6829 80.6687
29 44.8679 18.4201 29.6829 80.6687
30 44.8679 18.4201 29.6829 80.6687
31 44.8679 18.4201 29.6829 80.6687
32 44.8679 18.4201 29.6829 80.6687
33 44.8679 18.4201 29.6829 80.6687
34 44.8679 18.4201 29.6829 80.6687
35 44.8679 18.4201 29.6829 80.6687
36 44.8679 18.4201 29.6829 80.6687
37 44.8679 18.4201 29.6829 80.6687
38 44.8679 18.4201 29.6829 80.6687
39 44.8679 18.4201 29.6829 80.6687
40 44.8679 18.4201 29.6829 80.6687
41 44.8679 18.4201 29.6829 80.6687
42 44.8679 18.4201 29.6829 80.6687
43 44.8679 18.4201 29.6829 80.6687
44 44.8679 18.4201 29.6829 80.6687
45 44.8679 18.4201 29.6829 80.6687
46 44.8679 18.4201 29.6829 80.6687
47 44.8679 18.4201 29.6829 80.6687
48 44.8679 18.4201 29.6829 80.6687
49 44.8679 18.4201 29.6829 80.6687
50 44.8679 18.4201 29.6829 80.6687
当前最优解为: [80.6687431998708, 33.30888761832977, 29.682908594885962, 42.53006908649092, 38.149137170974406]
对应的函数最小值为: -30491.28458556166
静态惩罚
#!usr/bin/env python
# -*- coding:utf-8 _*-
"""
@author: liujie
@software: PyCharm
@file: 实际问题-死亡惩罚.py
@time: 2020/11/27 22:21
"""
'''
这个问题有5个变量,有6个非线性不等式约束和10个边界条件
'''
import numpy as np
import random
import matplotlib.pyplot as plt
from deap import creator, tools, base, algorithms
# 定义问题
creator.create('FitnessMin', base.Fitness, weights=(-1.0,))
creator.create('Individual', list, fitness=creator.FitnessMin)
# 个体编码-5个实数
# 变量下界
lb = [78, 33, 27, 27, 27]
# 变量上界
up = [102, 45, 45, 45, 45]
def uniform(lb, up):
return [random.uniform(a, b) for a, b in zip(lb, up)]
# 生成个体
toolbox = base.Toolbox()
toolbox.register('Attr_float', uniform, lb, up)
toolbox.register('Individual', tools.initIterate, creator.Individual, toolbox.Attr_float)
# 生成种群
pop_size = 100
toolbox.register('Population', tools.initRepeat, list, toolbox.Individual)
pop = toolbox.Population(n=pop_size)
# 评价函数
def himmelblauFun_StaticCons(ind):
return (5.3578547 * ind[2] * ind[2] + 0.8356891 * ind[0] * ind[4] + 37.293239 * ind[
0] - 40792.141 + 1000 * StaticCons(ind)),
# 施加约束
def StaticCons(ind):
# 判定解是否可行
g1 = 85.334407 + 0.0056858 * ind[1] * ind[4] + 0.00026 * ind[0] * ind[3] - 0.0022053 * ind[2] * ind[4]
g2 = 80.51249 + 0.0071317 * ind[1] * ind[4] + 0.0029955 * ind[0] * ind[1] + 0.0021813 * ind[2] * ind[2]
g3 = 9.300961 + 0.0047026 * ind[2] * ind[4] + 0.0012547 * ind[0] * ind[2] + 0.0019085 * ind[2] * ind[3]
cons = np.array([-g1, g1 - 92, -g2 + 90, g2 - 110, -g3 + 20, g3 - 25])
coefs = np.where(cons > 0, 1, 0)
return np.sqrt(np.sum(coefs * np.square(cons)))
# 注册评价函数
toolbox.register('evaluate', himmelblauFun_StaticCons)
# 注册进化过程中需要的工具:配种选择,交叉,变异
toolbox.register('select', tools.selTournament, tournsize=2) # 锦标赛
toolbox.register('mate', tools.cxSimulatedBinaryBounded, eta=20, low=lb, up=up)
toolbox.register('mutate', tools.mutPolynomialBounded, eta=20, low=lb, up=up, indpb=0.2)
# 创建统计对象
# 用数据记录算法迭代过程
stats = tools.Statistics(key= lambda ind : ind.fitness.values)
stats.register('avg', np.mean)
stats.register('std', np.std)
stats.register('min', np.min)
stats.register('max', np.max)
# 创建日志对象
logbook = tools.Logbook()
# 进化迭代,不妨设置如下参数
N_Gen = 50
CXPB = 0.8
MUTPB = 0.2
# 评价初代个体
fitnesses = map(toolbox.evaluate, pop)
for ind, fit in zip(pop, fitnesses):
ind.fitness.values = fit
record = stats.compile(pop)
logbook.record(gen=0, **record)
# 遗传算法迭代
for gen in range(1, N_Gen + 1):
# 配种选择
selectTour = toolbox.select(pop, pop_size)
# 复制个体,供交叉使用
selectInd = list(map(toolbox.clone, selectTour))
# print(selectInd)
# 对选出的个体两两进行交叉,对于被改变的个体,删除其适应度
for child1, child2 in zip(selectInd[::2], selectInd[1::2]):
if random.random() < CXPB:
toolbox.mate(child1, child2)
del child1.fitness.values
del child2.fitness.values
# 变异
for mutate in selectInd:
if random.random() < MUTPB:
toolbox.mutate(mutate)
del mutate.fitness.values
# 对于被改变的个体,重新计算其适应度
invalid_ind = [ind for ind in selectInd if not ind.fitness.valid]
fitnesses = map(toolbox.evaluate, invalid_ind)
for ind, fit in zip(invalid_ind, fitnesses):
ind.fitness.values = fit
# 精英育种-环境选择
combinedPop = pop + selectTour
pop = tools.selBest(combinedPop, pop_size)
# 记录数据-将stats注册功能应用于pop,并作为字典返回
record = stats.compile(pop)
logbook.record(gen=gen, **record)
# 输出计算过程
logbook.header = 'gen', 'avg', 'std', 'min', 'max'
print(logbook)
# 输出最优解
bestInd = tools.selBest(pop, 1)[0]
bestFit = bestInd.fitness.values[0]
print('当前最优解为:', str(bestInd))
print('对应的函数最小值为:', str(bestFit))
# 打印变化值
import matplotlib.pyplot as plt
# 用select方法从logbook提取迭代次数、最大值、均值
gen = logbook.select('gen')
fitness_min = logbook.select('min')
fitness_avg = logbook.select('avg')
fig = plt.figure()
fig.add_subplot()
plt.plot(gen, fitness_avg, 'r-', label='fitness_avg')
plt.plot(gen, fitness_min, 'b-', label='fitness_min')
plt.legend(loc='best')
plt.xlabel('gen')
plt.ylabel('fitness')
plt.tight_layout()
plt.show()
运行结果为
gen avg std min max
0 47.3522 21.6486 27.0249 101.074
1 45.601 21.7688 27.0249 100.847
2 44.4359 20.1038 27.0667 98.7299
3 43.945 19.502 27.1252 86.0796
4 43.3374 18.609 27.3512 83.3337
5 45.086 19.1474 27.3512 83.3337
6 46.2782 19.4158 27.3512 83.3337
7 46.2782 19.4158 27.3512 83.3337
8 46.2782 19.4158 27.3512 83.3337
9 46.2782 19.4158 27.3512 83.3337
10 46.2782 19.4158 27.3512 83.3337
11 46.2782 19.4158 27.3512 83.3337
12 46.2782 19.4158 27.3512 83.3337
13 46.2782 19.4158 27.3512 83.3337
14 46.2782 19.4158 27.3512 83.3337
15 46.2782 19.4158 27.3512 83.3337
16 46.2782 19.4158 27.3512 83.3337
17 46.2782 19.4158 27.3512 83.3337
18 46.2782 19.4158 27.3512 83.3337
19 46.2782 19.4158 27.3512 83.3337
20 46.2782 19.4158 27.3512 83.3337
21 46.2782 19.4158 27.3512 83.3337
22 46.2782 19.4158 27.3512 83.3337
23 46.2782 19.4158 27.3512 83.3337
24 46.2782 19.4158 27.3512 83.3337
25 46.2782 19.4158 27.3512 83.3337
26 46.2782 19.4158 27.3512 83.3337
27 46.2782 19.4158 27.3512 83.3337
28 46.2782 19.4158 27.3512 83.3337
29 46.2782 19.4158 27.3512 83.3337
30 46.2782 19.4158 27.3512 83.3337
31 46.2782 19.4158 27.3512 83.3337
32 46.2782 19.4158 27.3512 83.3337
33 46.2782 19.4158 27.3512 83.3337
34 46.2782 19.4158 27.3512 83.3337
35 46.2782 19.4158 27.3512 83.3337
36 46.2782 19.4158 27.3512 83.3337
37 46.2782 19.4158 27.3512 83.3337
38 46.2782 19.4158 27.3512 83.3337
39 46.2782 19.4158 27.3512 83.3337
40 46.2782 19.4158 27.3512 83.3337
41 46.2782 19.4158 27.3512 83.3337
42 46.2782 19.4158 27.3512 83.3337
43 46.2782 19.4158 27.3512 83.3337
44 46.2782 19.4158 27.3512 83.3337
45 46.2782 19.4158 27.3512 83.3337
46 46.2782 19.4158 27.3512 83.3337
47 46.2782 19.4158 27.3512 83.3337
48 46.2782 19.4158 27.3512 83.3337
49 46.2782 19.4158 27.3512 83.3337
50 46.2782 19.4158 27.3512 83.3337
当前最优解为: [83.33366786894811, 34.97045998251738, 27.351188353511365, 41.77050933971009, 43.96509532957687]
对应的函数最小值为: -30285.043888896478