点云分割和点云分类(点云语义分割)
目录
概念
点云分割(point cloud segmentation)
点云分类(point cloud classification)
特征提取
分割
物体识别
分类
常见点云分割方法
随机抽样一致算法(Random Sample Consensus,RANSAC)
算法流程
RANSAC与最小二乘区别
PCL中的 Sample_consensus 模块
欧式聚类分割(聚类)
区域生长算法(聚类)
基于颜色的区域生长分割(聚类)
最小图割的分割
基于法线微分的分割
基于超体素的分割
深度学习的分割方法
概念
点云分割(point cloud segmentation)
根据空间、几何和纹理等特征点进行划分,同一划分内的点云拥有相似的特征。
点云分割的目的是分块,从而便于单独处理。
点云分类(point cloud classification)
为每个点分配一个语义标记。点云的分类是将点云分类到不同的点云集。同一个点云集具有相似或相同的属性,例如地面、树木、人等。也叫做点云语义分割。
特征提取
单个点或一组点可以根据低级属性检测某种类型的点。
- “低级属性”是指没有语义(例如,位置,高程,几何形状,颜色,强度,点密度等)的信息。
- “低级属性 ”信息通常可以从点云数据中获取而无需事先的高级知识。例如,平面提取和边缘检测、以及特征描述子的 计算都可以视为特征提取过程。
分割
基于上述低级属性将点分组为一个部分或一个对象的过程。与单独对每个点处理或分析相比,分割过 程对每个对象的进一步处理和分析,使其具有更丰富的信息。
物体识别
识别点云中一种或多种类型对象的过程。该过程通常通过根据特征提取和分割的结果执行分析, 并基于先验知识在给定的约束和规则下进行。
分类
类似于对象识别的过程,该过程为每个点,线段或对象分配一个类别或标识,以表示某些类型的对象 (例如,标志,道路,标记或建筑物)。
对象识别和点云分类之间的区别在于:
- 对象识别是利用一种方法以将一些特定对象与其他对象区分开
- 分类的目的通常是在语义上标记整个场景。
点云的有效分割是许多应用的前提:
- 工业测量/逆向工程:对零件表面提前进行分割,再进行后续重建、计算特征等操作。
- 遥感领域:对地物进行提前分割,再进行分类识别等工作
常见点云分割方法
随机抽样一致算法(Random Sample Consensus,RANSAC)
采用迭代的方式从一组包含离群的被观测数据中估算出数学模型的参数。
RANSAC算法假设数据中包含正确数据和异常数据(或称为噪声)。
正确数据记为内点(inliers),异常数据记为外点(outliers)。
同时RANSAC也假设,给定一组正确的数据,存在可以计算出符合这些数据的模型参数的方法。该算法核心思想就是随机性和假设性:
- 随机性是根据正确数据出现概率去随机选取抽样数据,根据大数定律,随机性模拟可以近似得到正确结果。
- 假设性是假设选取出的抽样数据都是正确数据,然后用这些正确数据通过问题满足的模型,去计算其他点 ,然后对这次结果进行一个评分。
RANSAC算法被广泛应用在计算机视觉领域和数学领域,例如直线拟合、平面拟合、计算图像或点云间的变换矩阵、计算基础矩阵等方面,使用的非常多。
基于RANSAC的基本检测算法虽然具有较高的鲁棒性和效率,但是目前仅针对平面,球,圆柱体,圆锥和圆环物种基本的基元。
算法流程
- 要得到一个直线模型,需要两个点唯一确定一个直线方程。所以第一 步随机选择两个点。
- 通过这两个点,可以计算出这两个点所表示的模型方程y=ax+b。
- 将所有的数据点套到这个模型中计算误差。
- 找到所有满足误差阈值的点。
- 然后我们再重复1~4这个过程,直到达到一定迭代次数后,选出那个被 支持的最多的模型,作为问题的解。
Martin A. Fischler 和Robert C. Bolles于1981年发表在ACM期刊上的论文《Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography》
RANSAC与最小二乘区别
最小二乘法尽量去适应包括局外点在内的所有点。相 反,RANSAC能得出一个仅仅用局内点计算出模型, 并且概率还足够高。但是,RANSAC并不能保证结果 一定正确,为了保证算法有足够高的合理概率,必须小心的选择算法的参数(参数配置)。经实验验证, 对于包含80%误差的数据集,RANSAC的效果远优于直接的最小二乘法。
最重要的参数就是迭代的次数 k :
- 假设任取一个点是内群点的概率为
 ,则有
,则有  = 数 据中内群点的数量/数据中点的总数;
= 数 据中内群点的数量/数据中点的总数; - 则任取 n 个点都是内群点的概率为
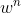 ;
; - 所以我们所选择的 n 个点至少有一个不是内群点的 概率为 1 −
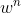 ;
; - 所以我们连续重复 k 次都不能有一次全是内群点的 概率 为
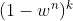 ;
; - 由上,我们发现当
 保持不变时,我们要想让尽 量小,则 n 越大,k 就需要越大
保持不变时,我们要想让尽 量小,则 n 越大,k 就需要越大
PCL中的 Sample_consensus 模块
PCL中的 Sample_consensus库实现了随机采样一致性及其泛化估计算法,以及例如平面、柱面等各种常见几何模型,用不同的估计算法和不同的几何模型自由结合估算点云中隐含的具体几何模型的系数, 实现点云中所处的几何模型的分割。
支持以下模型:
- SACMODEL_PLANE - 用于确定平面模型。平面的四个系数。
- SACMODEL_LINE - 用于确定线模型。直线的六个系数由直线上的一个点和直线的方向给出。
- SACMODEL_CIRCLE2D - 用于确定平面中的 2D 圆。圆的三个系数由其中心和半径给出。
- SACMODEL_CIRCLE3D - 用于确定平面中的 3D 圆。圆的七个系数由其中心、半径和法线给出。
- SACMODEL_SPHERE - 用于确定球体模型。球体的四个系数由其 3D 中心和半径给出。
- SACMODEL_CYLINDER - 用于确定气缸模型。圆柱体的七个系数由其轴上的点、轴方向和半径给出。
- SACMODEL_CONE - 用于确定锥模型。锥体的七个系数由其顶点、轴方向和张角给出。
- SACMODEL_TORUS - 尚未实施
- SACMODEL_PARALLEL_LINE -在最大指定角度偏差内确定与给定轴平行的线的模型。线系数类似于SACMODEL_LINE。
- SACMODEL_PERPENDICULAR_PLANE -在最大指定角度偏差内确定垂直于用户指定轴的平面的模型。平面系数类似于SACMODEL_PLANE。
- SACMODEL_PARALLEL_LINES - 尚未实现
- SACMODEL_NORMAL_PLANE - 使用附加约束确定平面模型的模型:每个内点的表面法线必须平行于输出平面的表面法线,在指定的最大角度偏差内。平面系数类似于SACMODEL_PLANE。
- SACMODEL_NORMAL_SPHERE - 类似于SACMODEL_SPHERE,但具有额外的表面法线约束。
- SACMODEL_PARALLEL_PLANE -在最大指定角度偏差内确定平行于用户指定轴的平面的模型。平面系数类似于SACMODEL_PLANE。
- SACMODEL_NORMAL_PARALLEL_PLANE使用附加表面法线约束定义 3D 平面分割模型。平面法线必须平行于用户指定的轴。因此,SACMODEL_NORMAL_PARALLEL_PLANE 等效于SACMODEL_NORMAL_PLANE + SACMODEL_PERPENDICULAR_PLANE。平面系数类似于SACMODEL_PLANE。
- SACMODEL_STICK - 3D 棒分割模型。一根棍子是一条给定用户最小/最大宽度的线。
以下列表描述了实现的稳健样本共识估计器:
- SAC_RANSAC - 随机样本共识
- SAC_LMEDS - 最小平方中位数
- SAC_MSAC - M-Estimator Sample Consensus
- SAC_RRANSAC - 随机 RANSAC
- SAC_RMSAC - 随机 MSAC
- SAC_MLESAC - 最大似然估计样本共识
- SAC_PROSAC - 渐进式样本共识
//创建一个模型参数对象,用于记录结果
pcl::ModelCoefficients::Ptr coefficients (new pcl::ModelCoefficients);
//inliers表示误差能容忍的点 记录的是点云的序号
pcl::PointIndices::Ptr inliers (new pcl::PointIndices);
// 创建一个分割器
pcl::SACSegmentation seg;
// Optional seg.setOptimizeCoefficients (true);
// Mandatory-设置目标几何形状
seg.setModelType (pcl::SACMODEL_PLANE);
//分割方法:随机采样法seg.setMethodType (pcl::SAC_RANSAC);
//设置误差容忍范围seg.setDistanceThreshold (0.01);
//输入点云seg.setInputCloud (cloud);
//分割点云,得到参数
seg.segment (*inliers, *coefficients);
Schnabel R, Wahl R, Klein R. Efficient RANSAC for point‐cloud shape detection[C]//Computer graphics forum. Oxford, UK: Blackwell Publishing Ltd, 2007, 26(2): 214-226.
https://cg.cs.uni-bonn.de/en/publications/paper-details/schnabel-2007-efficient/
欧式聚类分割(聚类)
聚类方法,通过特征空间确定点与点之间的亲疏程度
算法流程:
- 找到空间中某点p,有kdTree找到离他最近的n个点,判断这n个点到p的距离。将距离小于阈值r的点p1,p2,p3... 放在类Q里
- 在 Q里找到一点p1,重复1,找到p22,p23,p24 全部放进Q里
- 当 Q 再也不能有新点加入了,则完成搜索了
pcl::EuclideanClusterExtraction ec;
ec.setClusterTolerance (0.02); ec.setMinCl
usterSize (100);
ec.setMaxClusterSize (25000); ec.setSearchMethod (tree); ec.setInputCloud (cloud_filtered); ec.extract (cluster_indices);
使用类pcl::ConditionEuclideanClustering实现点云分割,与其他分割方法不同的是该方法的聚类约束条件(欧式距离、平滑度、RGB颜色等)可以由用户自己定义,即当搜索到一个近邻点时,用户可以自定义该邻域点是否合并到当前聚类的条件。
pcl::ConditionalEuclideanClustering cec (true);//创建条件聚类分割对象,并进行初始化。cec.setInputCloud (cloud_with_normals);//设置输入点集
//用于选择不同条件函数
switch(Method)
{
case 1:
cec.setConditionFunction (&enforceIntensitySimilarity); break;
case 2:
cec.setConditionFunction (&enforceCurvatureOrIntensitySimilarity); break;
case 3:
cec.setConditionFunction (&customRegionGrowing); break;
default:
cec.setConditionFunction (&customRegionGrowing); break;
}
cec.setClusterTolerance (500.0);//设置聚类参考点的搜索距离
cec.setMinClusterSize (cloud_with_normals->points.size () / 1000);//设置过小聚类的标准cec.setMaxClusterSize (cloud_with_normals->points.size () / 5);//设置过大聚类的标准cec.segment (*clusters);//获取聚类的结果,分割结果保存在点云索引的向量中
cec.getRemovedClusters (small_clusters, large_clusters);//获取无效尺寸的聚类
这个条件的设置是可以由我们自定义的,因为除了距离检查,聚类的点还需要满足一个特殊的自定义的要 求,就是以第一个点为标准作为种子点,候选其周边的点作为它的对比或者比较的对象,如果满足条件就加入到聚类的对象中。
//如果此函数返回true,则将添加候选点到种子点的簇类中。
bool customCondition(const pcl::PointXYZ& seedPoint, const pcl::PointXYZ& candidatePoin t, float squaredDistance) {
// 在这里你可以添加你自定义的条件
return false;
return true;
}区域生长算法(聚类)
区域生长算法: 将具有相似性的点云集合起来构成区域。
首先对每个需要分割的区域找出一个种子点作为生长的起点,然后将种子点周围邻域中与种子有相同或相似性质的点合并到种子像素所在的区域中。而新的点继续作为种子向四周生长,直到再没有满足条件 的像素可以包括进来,一个区域就生长而成了。
算法流程:
- 计算 法线normal 和 曲率curvatures,依据曲率升序排序;
- 选择曲率最低的为初始种子点,种子周围的临近点和种子点云相比较;
- 法线的方向是否足够相近(法线夹角足够 r p y), 法线夹角阈值;
- 曲率是否足够小(表面处在同一个弯曲程度),区域差值阈值;
- 如果满足2,3则该点可用做种子点;
- 如果只满足2,则归类而不做种子;
算法是针对小曲率变化面设计的,尤其适合对连续阶梯平面进行分割。
//区域增长聚类分割对象 < 点 , 法 线 >
pcl::RegionGrowing reg;
reg.setMinClusterSize (50); //最小的聚类的点数
reg.setMaxClusterSize (1000000);//最大的聚类的点数
reg.setSearchMethod (tree); //搜索方式
reg.setNumberOfNeighbours (30); //设置搜索的邻域点的个数
reg.setInputCloud (cloud); //输入点
//reg.setIndices (indices);
reg.setInputNormals (normals); //输入的法线
reg.setSmoothnessThreshold (3.0 / 180.0 * M_PI);//设置平滑度 法线差值阈值
reg.setCurvatureThreshold (1.0); //设置曲率的阀值
基于颜色的区域生长分割(聚类)
基于颜色的区域生长分割
基于颜色的区域生长分割原理上和基于曲率,法线的分割方法是一致的,只不过比较目标换成了颜色。可以认为,同一个颜色且挨得近,是一类的可能性很大,比较适合用于室内场景分割。尤其是复杂室内场景,颜色分割可以轻松的将连续的场景点云变成不同的物体。哪怕是高低不平的地面,设法用采样一致分割器抽掉平面,颜色分割算法对不同的颜色的物体实现分割。
算法主要分为两步:
- 分割,当前种子点和领域点之间色差小于色差阀值的视为一个聚类。
- 合并,聚类之间的色差小于色差阀值和并为一个聚类,且当前聚类中点的数量小于聚类点数量的与最近的聚类合并在一起。
RBG的距离
//基于颜色的区域生成的对象
pcl::RegionGrowingRGB reg;
reg.setInputCloud (cloud);
reg.setIndices (indices); //点云的索引
reg.setSearchMethod (tree);
reg.setDistanceThreshold (10);//距离的阀值
reg.setPointColorThreshold (6);//点与点之间颜色容差
reg.setRegionColorThreshold (5);//区域之间容差
reg.setMinClusterSize (600); //设置聚类的大小
std::vector clusters;
reg.extract (clusters);//
pcl::PointCloud ::Ptr colored_cloud = reg.getColoredCloud (); 最小图割的分割
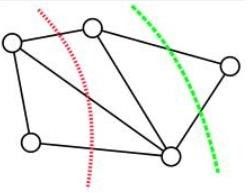
图论中的最小割(min-cut) 广泛应用在网络规划,求解桥问题,图像分割等领域。
最小割算法是图论中的一个概念,其作用是以某种方式,将两个点分开,当然这两个点中间可能是通过无数的点再相连的。 如果要分开最左边的点和最右边的点,红绿两种割法都是可行的, 但是红线跨过了三条线,绿线只跨过了两条。单从跨线数量上来论可以得出绿线这种切割方法更优的结论。但假设线上有不同的权值,那么最优切割则和权值有关了。
http://gfx.cs.princeton.edu/pubs/Golovinskiy_2009_MBS/paper_small.pdf
算法主要思想:
- 建图:对于给定的点云,算法将包含点云中每一个点的图构造为一组普通顶点和另外两个称为源点和汇点的顶点。每个普通顶点都有边缘,将对应的点与其最近的邻居连接起来。
- 算法为每条边缘分配权重。有三种不同的权:首先,它将权重分配到云点之间的边缘。这个权重称为平滑成本,由公式计算:
这里dist是点之间的距离。距离点越远,边被切割的可能性就越大。
3.算法设置数据成本。它包括前景和背景惩罚。第一个是将云点与源顶点连接起来并具有用户定义的常量值的边缘的权重。
对点云的前景点和背景点进行划分。
// 申明一个Min-cut的聚类对象pcl::MinCutSegmentation clustering; clustering.setInputCloud(cloud); //设置输入
//创建一个点云,列出所知道的所有属于对象的点
// (前景点)在这里设置聚类对象的中心点(想想是不是可以可以使用鼠标直接选择聚类中心点的方法呢?) pcl::PointCloud::Ptr foregroundPoints(new pcl::PointCloud()); pcl::PointXYZ point;
point.x = 100.0;
point.y = 100.0;
point.z = 100.0;
foregroundPoints->points.push_back(point);
clustering.setForegroundPoints(foregroundPoints);//设置聚类对象的前景点
//设置sigma,它影响计算平滑度的成本。它的设置取决于点云之间的间隔(分辨率) clustering.setSigma(0.02);// cet cost = exp(-(dist/cet)^2)
// 设 置 聚 类 对 象 的 半 径 . clustering.setRadius(0.01);// dist2Center / radius
//设置需要搜索的临近点的个数,增加这个也就是要增加边界处图的个数
clustering.setNumberOfNeighbours(20);
//设置前景点的权重(也就是排除在聚类对象中的点,它是点云之间线的权重,) clustering.setSourceWeight(0.6);
std::vector clusters; clustering.extract(clusters);
基于法线微分的分割
根据不同尺度下法向量特征的差异性,利用pcl::DifferenceOfNormalsEstimation实现点云分割,在处理有较大尺度变化的场景点云分割效果较好,利用不同支撑半径去估算同一点的两个单位法向量,单位法向量的差定义DoN特征
DoN算法:
DoN特征源于观察到基于所给半径估计的表面法向量可以反映曲面的内在几何特征,因此这种分割算法是基于法线估计的,需要计算点云中某一点的法线估计。而通常在计算法线估计的时候都会用到邻域信息,很明显邻域大小的选取会影响法线估计的结果。
而在DoN算法中,邻域选择的大小就被称为support radius。对点云中某一点选取不同的支持半径,即可以得到不同的法线估计,而法线之间的差异,就是是所说的法线差异。
PCL_点云分割_基于法线微分分割
算法流程:
- 对于输入点云数据中的每一点,利用较大的支撑半径计算法向量;
- 对于输入点云数据中的每一点,利用较大的支撑半径计算法向量;
- 对于输入点云数据中的每一点,单位化每一点的法向量差异
- 过滤所得的向量域(DoN特征向量),分割出目标尺寸对应的点云;
// Create output cloud for DoN results
PointCloud::Ptr doncloud (new pcl::PointCloud); copyPointCloud(*cloud, *doncloud);
pcl::DifferenceOfNormalsEstimation do
n;
don.setInputCloud (cloud);
don.setNormalScaleLarge (normals_large_scale);
don.setNormalScaleSmall (normals_small_scale); don.initCompute ();
// Compute DoN
don.computeFeature (*doncloud);
Difference of Normals as a Multi-Scale Operator in Unorganized Point Clouds
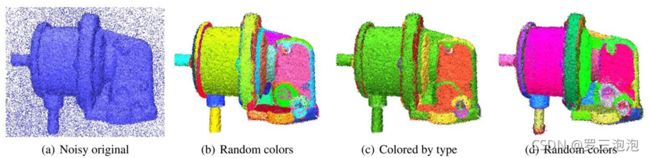
基于超体素的分割
超体(super voxel)是一种集合,集合的元素是“体素”。
与体素滤波器中的体类似,其本质是一个个的小方块。与之前提到的所有分割手段不同,超体聚类的目的 并不是分割出某种特定物体,其对点云实施过分割(over segmentation),将场景点云化成很多小块,并 研究每个小块之间的关系。
以八叉树对点云进行划分,获得不同点团之间的邻接关系。与图像相似,点云的邻接关系也有很多,如面 邻接、线邻接、点邻接。
【PCL】—超体聚类点云分割算法详解
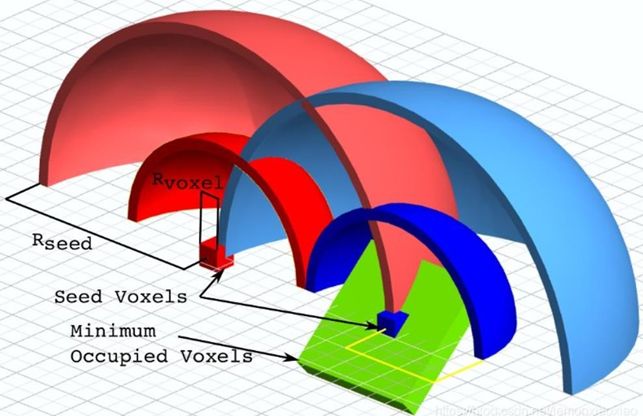
超体聚类实际上是一种特殊的区域生长算法,和无限制的生长不同,超体聚类首先需要规律的布置区域生长“晶核”。晶核在空间中实际上是均匀分布的,并指定晶核距离(Rseed),再指定粒子距离(Rvoxel),再指定最小晶粒(MOV),过小的晶粒需要融入最近的大晶粒。
有了晶粒和结晶范围之后,我们只需要控制结晶过程,就能将整个空间划分开了。结晶过程的本质就是不断吸纳类似的粒子(八分空间)。类似是一个比较模糊的概念,关于类似的定义有以下公式:
公式中的Dc表示颜色上的差异,Dn表示法线上的差异,Ds代表点距离上的差异。w表示一系列权重,用于控制结晶形状。在晶核周围寻找一圈,D最小的体素被认为是下一个“被发展的对象”。
需要注意的是,结晶过程并不是长完一个晶核再长下一个,而是所有的晶核同时开始生长。接下来所有晶核继续公平竞争,发展第二个“对象”,以此循环。最终所有晶体应该几乎同时完成生长,整个点云也被晶格所分割开来,并且保证了一个晶包里的粒子都是类似的。
//生成结晶器
pcl::SupervoxelClustering super(voxel_resolution, seed_resolution);
//和点云形式有关if(disable_transform)
super.setUseSingleCameraTransform(false);
//输入点云及结晶参数
super.setInputCloud(cloud);
super.setColorImportance(color_importance);
super.setSpatialImportance(spatial_importance); super.setNormalImportance(normal_importance);
//输出结晶分割结果:结果是一个映射表
std::map ::Ptr > supervoxel_clusters; super.extract(supervoxel_clusters); //获得晶体中心
PointCloudT::Ptr voxel_centroid_cloud = super.getVoxelCentroidCloud(); //获得晶体
PointLCloudT::Ptr labeled_voxel_cloud = super.getLabeledVoxelCloud();
深度学习的分割方法
深度学习是当前模式识别,计算机视觉和数据分析中最有影响力,发展最快的前沿技术。
2、基于体素
3、端到端-直接对点云进行处理
Guo Y, Wang H, Hu Q, et al. Deep learning for 3d point clouds: A survey[J]. IEEE transactions on pattern analysis and machine intelligence, 2020.
Guo Y, Wang H, Hu Q, et al. Deep learning for 3d point clouds: A survey[J]. IEEE transactions on pattern analysis and machine intelligence, 2020.