平面三自由度机器人动力学建模与仿真

网上二自由度机器臂动力学分析有很多，三自由度比较少，碰巧本科课设需要完成相关项目，分享一些经验供参考。

机器臂建模

实际的三连杆机器臂的结构相对较复杂，很难进行精确地描述，因此，在本文中利用简化的数学模型进行讨论。简化条件如下：

1. 假设机器臂是刚性结构，不考虑形变；
2. 忽略各构件之间的摩擦力；
3. 假设机器臂的连杆是密度均匀的刚体。

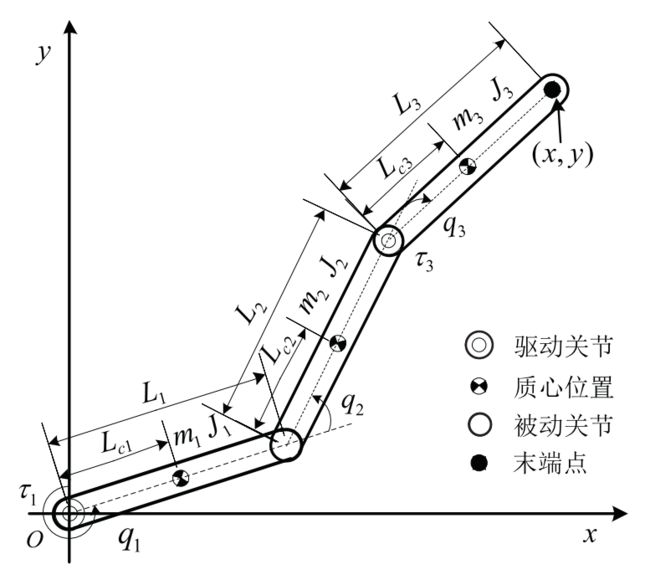
平面三连杆机器臂模型结构如图1所示， $m_i$ 为第 $i$ 杆的质量， $L_i$ 为 $i$ 杆的长度，$L_{ci}$ 为 $i$ 杆的质心到前一关节的长度，$J_i$ 为第 $i$ 杆的转动惯量。

对于平面三连杆机器臂而言， $q_1$ 、 $q_2$ 和 $q_3$ 唯一地确定了其位置， $q_1$ 、 $q_2$ 和 $q_3$ 的一阶导数和二阶导数确定了其运动状态，它们是动力学描述所需的基础变量。

1、拉格朗日方程

平面三连杆机器臂的拉格朗日算子为动能和势能之差，即：

$$L(q,\dot{q})=T(q,\dot{q})-U(q)$$
其中， $T(q,\dot{q})$ 和 $U(q)$ 分别是机器臂的动能和势能。

基于上面的拉格朗日算子，可得到平面三连杆机器臂的拉格朗日动力学方程为：
$$\frac{d}{dt}\frac{\partial }{\partial {\dot{q}}_i}L(q,\dot{q})-\frac{\partial }{\partial q_i}L(q,\dot{q})={\tau }_i$$
其中， ${\tau }_i$ 是作用在第 $i$ 杆的驱动力矩。进一步化简拉格朗日方程可以进一步表达为：
$$\frac{d}{dt}\frac{\partial }{\partial {\dot{q}}_i}T(q,\dot{q})-\frac{\partial }{\partial q_i}T(q,\dot{q})+\frac{\partial }{\partial q_i}U(q)={\tau }_i$$

2、动力学模型

将拉格朗日方程写成动力学方程的表达方式：
$$M(q)\ddot{q}+C(q,\dot{q})+G(q)=\tau$$
其中， $\tau ={\left[\begin{array}{ccc}{\tau }_1& {\tau }_2& {\tau }_3\end{array}\right]}^T$ 是控制力矩向量， $\ddot{q}={\left[\begin{array}{ccc}{\ddot{q}}_1& {\ddot{q}}_2& {\ddot{q}}_3\end{array}\right]}^T$ 是系统的角加速度向量，$M(q)\in R^{3\times 3}$ 是惯性矩阵，具有正定性和对称性， $C(q,\dot{q})\in R^{3\times 1}$ 是哥式力和离心力的结合向量，$G(q)\in R^{3\times 1}$ 是重力矩阵。它们的具体形式如下：
$$M(q)=\left[\begin{array}{ccc}{M}_{11}& M_{12}& M_{13}\\ M_{21}& M_{22}& M_{23}\\ M_{31}& M_{32}& M_{33}\end{array}\right]$$

$$C(q,\dot{q})=\left[\begin{array}{c}{C}_1\\ C_2\\ C_3\end{array}\right]$$

$$G(q)=\left[\begin{array}{c}{G}_1\\ G_2\\ G_3\end{array}\right]$$

其中， $M(q)$ 中的系数如下：
$$\{\begin{array}{l}{M}_{11}=a_1+a_2+a_4+2a_3\cos q_2+2a_5\cos (q_2+q_3)+2a_6\cos q_3,\\ M_{12}=a_2+a_4+a_3\cos q_2+\cos (q_2+q_5)+2a_6\cos q_3,\\ M_{13}=a_4+a_5\cos (q_2+q_3)+a_6\cos q_3,\\ M_{21}=M_{12},\\ M_{22}=a_2+a_4+2a_6\cos q_3,\\ M_{23}=a_4+a_6\cos q_3,\\ M_{31}=M_{13},\\ M_{32}=M_{23},\\ M_{33}=a_4.\end{array}$$
其中： $a_i(i=1,2,...,6)$ 是系统的结构参数，有
$$\{\begin{array}{l}{a}_1=m_1{L}_{c1}^2+J_1+(m_2+m_3)L_1^2,\\ a_2=J_2+m_2{L}_{c2}^2+m_3{L}_2^2,\\ a_3=(m_2{L}_{c2}+m_3{L}_2)L_1,\\ a_4=J_3+m_3{L}_{c3}^2,\\ a_5=m_3{L}_{c3}{L}_1,\\ a_6=m_3{L}_{c3}{L}_2.\end{array}$$
其中， $C(q,\dot{q})$ 中的系数如下：
$$\{\begin{array}{l}{C}_1=-a_3(2{\dot{q}}_1+{\dot{q}}_2){\dot{q}}_2\sin q_2-a_5(2{\dot{q}}_1+{\dot{q}}_2+{\dot{q}}_3)({\dot{q}}_2+{\dot{q}}_3)\sin (q_2+q_3)-\\ a_6(2{\dot{q}}_1+2{\dot{q}}_2+{\dot{q}}_3){\dot{q}}_3\sin q_3,\\ C_2=a_3{\dot{q}}_1^2\sin q_2+a_5{\dot{q}}_1^2\sin (q_2+q_3)-a_6(2{\dot{q}}_1+2{\dot{q}}_2+{\dot{q}}_3){\dot{q}}_3\sin q_3,\\ C_3=a_5{\dot{q}}_1^2\sin (q_2+q_3)+a_6({\dot{q}}_1+{\dot{q}}_2{)}^2\sin q_3.\end{array}$$
其中， $G(q)$ 中的系数如下：
$$\{\begin{array}{l}{G}_1=m_{3}g[L_1\cos q_1+L_2\cos (q_1+q_2)+L_{c3}\cos (q_1+q_2+q_3)]+\\ m_{2}g[L_1\cos q_1+L_{c2}\cos (q_1+q_2)]+m_{1}g[L_{c1}\cos q_1],\\ G_2=m_{3}g[L_2\cos (q_1+q_2)+L_{c3}\cos (q_1+q_2+q_3)]+\\ m_{2}g[L_{c2}\cos (q_1+q_2)],\\ G_3=m_{3}g[L_{c3}\cos (q_1+q_2+q_3)].\end{array}$$
至此，平面三连杆机器臂的动力学模型建立完成，动力学方程的形式体现出机器臂系统是一个具有强耦合和非线性的复杂系统，系统在运动过程中，各个关节相互影响。基于拉格朗日方程得到的机器臂动力学模型的建立起了机器臂关节驱动力矩与机器臂运动参数和机械参数之间的关系，为机器臂系统PD控制算法提供了基础。

控制器设计

对于自由运动机器人来说，其控制器设计可以按是否考虑机器人的动力学特性分两类：一类是完全不考虑机器人的动力学特性，只是按照机器人实际轨迹与期望轨迹间的偏差进行负反馈控制；另一类控制器设计方法被称为动态控制,这类方法是根据机器人动力学模型的性质设计出更精细的非线性控制律，所以又常称为以模型为基础的控制。

本文采用的是动态控制中的PD控制律，机器人的动力学方程为：
$$M(q)\ddot{q}+C(q,\dot{q})+G(q)=\tau$$
当给定连杆参数时，可以计算出 $M(q)$ 、 $C(q,\dot{q})$ 、$G(q)$ 的估计值 $\hat{M}(q)$ 、 $\hat{C}(q,\dot{q})$ 、 $\hat{G}(q)$ 。以 $u=\ddot{q}$ 作为新的输入量来考虑下列非线性反馈控制律：
$$\tau =\hat{M}(q)u+\hat{C}(q,\dot{q})+\hat{G}(q)$$
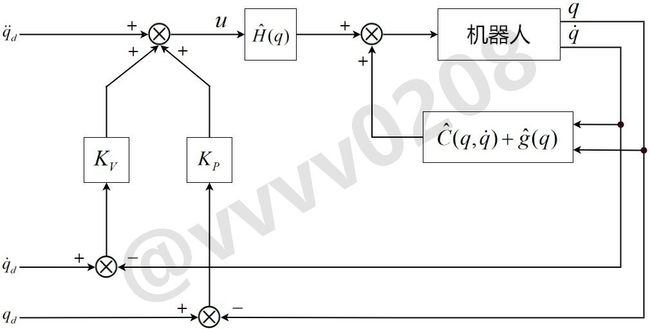
如果估计值全为正值，目标轨迹的关节期望加速度为 ${\ddot{q}}_d$ ，并取 $u=\ddot{q}$ ，于是可以完全实现目标轨迹的跟踪任务，这种考虑方法称为转矩计算法。但是，通常机器人的物理参数的估计值不可能完全正确，所以本文采用下图所示的PD反馈控制律：

这时，如果考虑用下式表示轨迹误差
$$e=q_d-q$$
可以得出
$$\ddot{e}+K_V\dot{e}+K_{P}e=0$$
对于该式，通过适当地设定 $K_p$ 和 $K_v$ 就有可能使轨迹误差收敛到0。

机器臂轨迹规划

关节空间轨迹规划的基本方法是通过机器臂逆运动学，将机器臂末端操作手中心点所要经过的空间位置转换成各个关节对应的关节角度。本文采用的方法是，利用逆运动学计算出各个空间位置所对应的关节角度，对每两个位置的关节角度之间进行多项式插值，然后各个关节按照所规划的角度变化曲线进行动。

基于三次多项式插值法的轨迹规划算法不能保证各个点之间速度曲线的平滑过渡，这样的速度和加速度曲线在机器臂应用过程中产生一些不利影响，为获得在各个点之间过渡平滑的速度曲线，继续增加初始和终止的加速度边界条件，此时需要采用五次多项式对运行轨迹进行规划：
$$\begin{array}{l}q(t)=q_0+b_1(t-t_0)+b_2(t-t_0{)}^2+b_3(t-t_0{)}^3+b_4(t-t_0{)}^4+b_5(t-t_0{)}^5\end{array}$$
根据条件有：
$$\{\begin{array}{l}q(t_0)=q_{0}q(t_1)=q_1\\ \dot{q}(t_0)=v_0\dot{q}(t_1)=v_1\\ \ddot{q}(t_0)=a_0\ddot{q}(t_1)=a_1\end{array}$$
令$h=q_1-q_0\tau =t_1-t_0$ ，求的多项式系数为：
$$\{\begin{array}{l}{b}_0=q_0,\\ b_1=v_0,\\ b_2=\frac{1}{2}{a}_0,\\ b_3=\frac{20h-(8v_1+12v_0)\tau -(3a_0-a_1){\tau }^2}{2{\tau }^3},\\ b_4=\frac{-30h+(14v_1+16v_0)\tau +(3a_0-2a_1){\tau }^2}{2{\tau }^4},\\ b_5=\frac{12h-(6v_1+6v_0)\tau +(-a_0+a_1){\tau }^2}{2{\tau }^5}.\end{array}$$

机器臂仿真

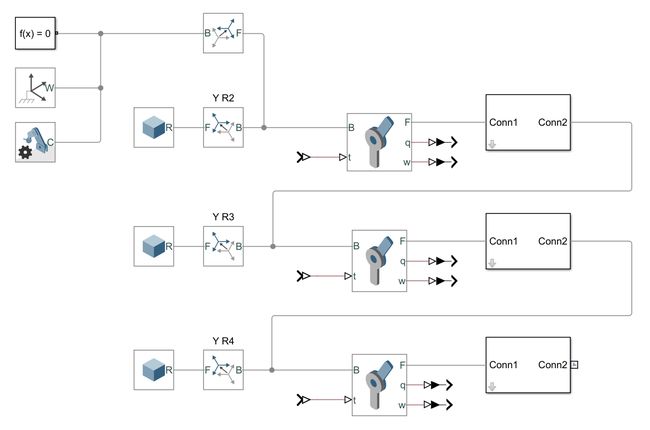
在 MATLAB 中建立三连杆系统模型。由于考虑机器人系统的重力模型引入了非线性项目，故采用 Simscape 建立仿真模型如下图所示。

建立起来的模型示意图如下（这个是robot toolbox工具箱生成，并非Simscape生成）：

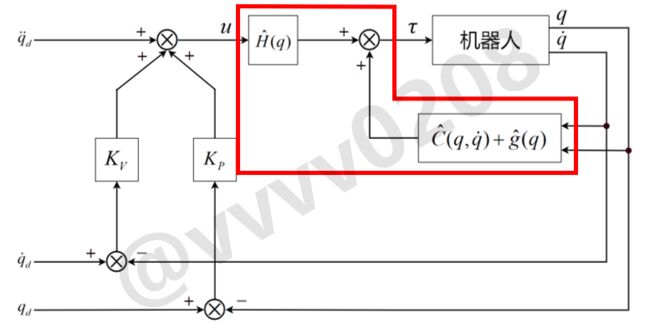
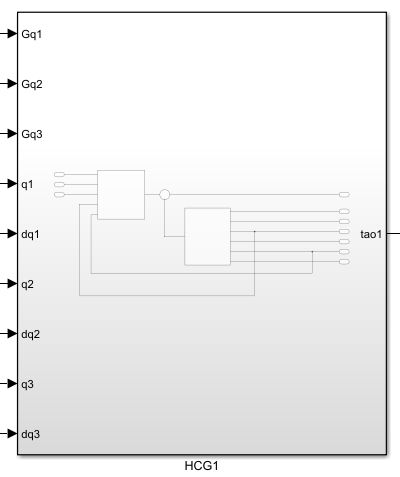
以第一个连杆为例，建立第一个连杆的力矩估计，

对应方框图中红色框中的模型如下：

H1代码，这部分就是之前求得的动力学方程

function y = fcn(Gddq1,Gddq2,Gddq3,q2, q3, a1, a2, a3, a4, a5, a6)
h11 = a1+a2+a4+2*a3*cos(q2)+2*a5*cos(q2+q3)+2*a6*cos(q3);
h21 = a2+a4+a3*cos(q2)+a5*cos(q2+q3)+2*a6*cos(q3);
h31 = a4+a5*cos(q2+q3)+a6*cos(q3);
y = Gddq1*h11+Gddq2*h21+Gddq3*h31;

CG1代码

function y = fcn(q1, dq1, q2, dq2, q3, dq3, a1, a2, a3, a4, a5, a6, L1, Lc1, L2, Lc2, Lc3, m1, m2, m3)
C1 = -a3*(2*dq1+dq2)*dq2*sin(q2) - a5*(2*dq1+dq2+dq3)*(dq2+dq3)*sin(q2+q3) ...
     -a6*(2*dq1+2*dq2+dq3)*dq3*sin(q3);
G1 = m3*9.8*(L1*cos(q1)+L2*cos(q1+q2)+Lc3*cos(q1+q2+q3)) + m2*9.8*(L1*cos(q1)+Lc2*cos(q1+q2)) ...
     +m1*9.8*Lc1*cos(q1);
y = C1+G1;

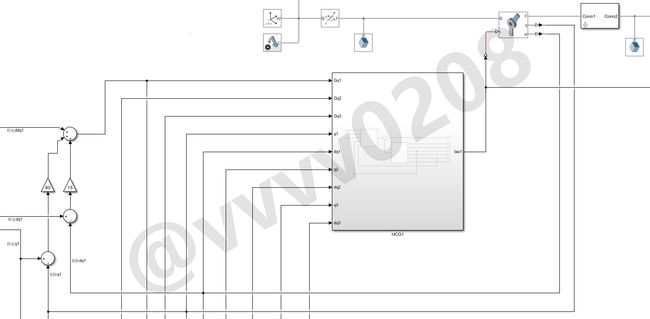
将上面的封装，如下

第一个关节的全部仿真模型如下，其中左边为PD控制器，上面为使用 Simscape 搭建模拟机器臂

仿真结果

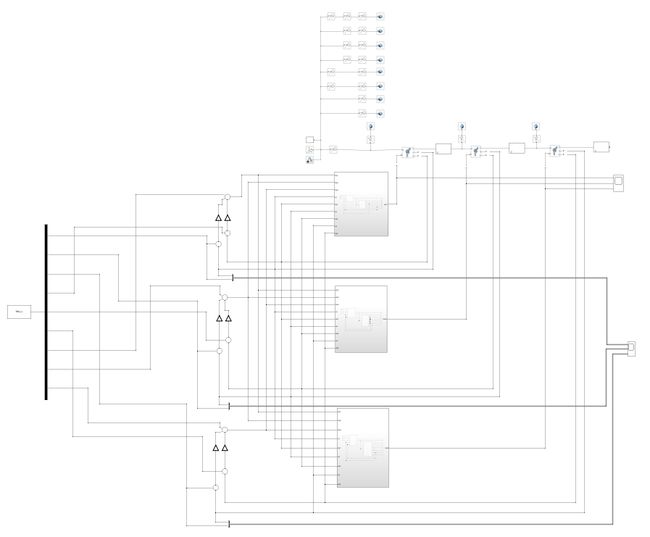
将三个关节都搭建起来（方法同第一个关节），大致如下：

示波器输出每个关节角度跟踪情况

加了一些场景布置，三层隔板，机器臂对一和三层进行访问（假装），仿真结果动态图

上图仿真的下载链接如下（需要安装robot toolbox，压缩包内已包括安装包和安装教程）：

https://download.csdn.net/download/qq_35231630/74358490

稍作改进就可以实现如下效果（这个就不放链接了）

未经本文允许不得转载。