从指数构建原理看待A股的三千点魔咒
摘要与声明
1:本文主要对指数构建方式进行简单介绍,并利用等权加权,基本面加权及防御型策略的方式对上证指数进行重构;
2:本文主要为理念的讲解,模型也是笔者自建,文中假设与观点是基于笔者的一孔之见,若有不同见解欢迎随时留言交流;
3:笔者希望搭建出一套交易体系,原则是只做干货的分享。后续将更新更多内容,但工作学习之余的闲暇时间有限,更新速度慢还请谅解;
4:本文主要数据通过Tushare(ID:444829)金融大数据平台接口获取;
5:模型实现基于python3.8;
A股指数编制方法改革已经过去近一年半了,笔者记得当时不少财经文章预测指数重编之后A股有极大可能将进入“指数牛”。目前仅过去一年半时间,指数的表现依然不佳,市场上依然很多人不禁感叹指数失真。本期笔者从指数构建原理出发,回答三个问题:1)为什么有失真的感觉;2)A股不涨是不是因为指数失真;3)A股指数构建方式是否合理。然后笔者利用几种不同的指数构建方法对上证指数重构并对结果进行分析,最后对未来做出展望。本文主要内容如下:
目录
1. 指数构建方法
2. 三问三答
2.1 为什么有失真的感觉
2.2 焊牢三千点是因为指数失真吗
2.3 A股指数构建方式是否合理
3. 上证指数重构
3.1 重构原则
3.2 代码实现
1):等权加权指数
2):PE加权指数
3):PE反向加权指数
4):PB加权指数
5):防御型策略指数
4. 未来展望
5. 附录
1. 指数构建方法
指数构建的统计方式有两种:全市场法(Exhaustive strategy)和抽样法(Selective approach)。例如道琼斯指数就是以30家公司作为总体进行全市场指数编制,而改革之后上证指数及深证成指都是有抽样的指数编制方法。
指数点位的计算主要有四种常见的方式:市值加权,等权加权,价格加权和基本面加权,以及一些较为少见的方式及策略,例如,防御型策略(Defensive strategy),波动率平滑策略(Volatility reducing strategy),包含:波动率加权(Volatility weighting),均值方差最优指数(Minimum-variance index)等。有些是笔者自己翻译的,感觉更贴切一些,因此可能和中文文献上看见的名字不太一样。 前面几种最为简单,相信不少人都知道原理,不过出于内容完整性考虑,笔者还是依次带一下以上所有构建方式的原理及特点:
1):市值加权,是A股绝大部分指数所采用的加权方式,通过统计范围内每家公司的市值占比对每日涨跌或价格进行加权平均后得到指数涨跌幅或指数点位。这其中又分为流通市值和总市值加权。如果按照外资能否进行投资又可以划分出自由流通市值加权,例如创业板就是这样的加权方式。
优点:体现市场流动性;体现大市值公司特点;便于被动跟踪投资;体现投资者投资能力(想买的都能按市值比例买到)。
缺点:小市值公司被低配。
2):价格加权,直接利用价格进行算术平均计算指数点位,道琼斯工业指数就是这种加权方式。
优点:计算简单;体现高价股特点。
缺点:如果有公司进行拆股并股,需要频繁调整除数;指数偏向于高价股,低价股被低配。
3):等权加权,每家公司买入同等金额计算点位数,或对统计范围内所有公司涨跌幅进行算术平均计算涨跌幅。
优点:较为均衡体的现所有公司状态,分散化程度高(集中程度低),修正了市值加权和价格加权对某类公司的偏差。
缺点:难以完美进行被动投资,要求每家公司买入同等金额是很难实现的;被动投资交易成本高,股票在交易时价格一直在变化,也就是说为了维持等权加权需要不断做指数再平衡(Re balancing);不一定能体现投资者的投资能力(想买的不一定能等权比例完全买到)。
4):基本面加权,采用基本面因子,例如PE,ROA,ROE,净利率等指标进行加权。
优点:适用于当前市场有效性差,定价不公允的情况,基本面因子具有基本面修正作用,更能体现成分股基本面状况。
缺点:很多基本面因子自带缺点属性,例如财务指标有滞后,容易被操纵的特点;不同人对基本面看法也不尽相同,因此很多加权方式难以被大众所接受,这种加权方式更多是分析师自建,用于修正和分析当前市场。
下面还有几种非常少见的指数构建方式,大多数是用于给特殊需求的合格投资者准备的特色指数,它们优缺点也是类似的:
5):防御型策略(Defensive strategy),对于一些风险厌恶型的投资者,可以采用超配防御性公司,例如利用分红率加权超配分红很高的公司,利用现金流比率超配现金流稳定的公司。原理上还是基本面加权的那一套,但配置的出发点及逻辑和基本面加权不太一样。
6):波动率加权(Volatility weighting),对于一些风险厌恶型的投资者,可以采用波动率倒数加权,超配低波动率公司,低配高波动率公司。
7):均值方差最优指数(Minimum-variance index),利用有效前沿利率找风险回报更优的组合,这里的权重配置涉及到有效前沿,就不展开了。
优点:能满足特定投资者需求;能帮助被动投资者抵抗市场下沉。
缺点:很小众的方式,难以为大众所接受。
2. 三问三答
在了解上面各种构建方式的特性后,不妨重新审视A股的指数构建方式。先说结论:笔者认为A股当前采取的市值加权是不错的方式。虽然市值加权有一定缺点,但除了上面所例举的市值加权的优点,它还拥有便利性高,公众接受程度高,维护金融市场稳定性等特点,采用其它方法很难达到市值加权这样的效果。
2.1 为什么有失真的感觉
笔者认为失真的感觉与指数构建方法有关。上证指数2千多支成分股,而大市值公司始终是少数。我们在日常选股的过程中大概率选到的都是那些较小市值的公司,于是有意思的现象就产生了:茅台,几个大银行,还有两桶油这些巨无霸权重个股只要涨一涨指数基本跌不到哪里去,但较小市值公司确跌得轰轰烈烈。这种现象在市场存量博弈的结构性行情尤为明显,指数还红着,打开自选却绿了一片,于是很多人开始感叹指数“失真”。
2.2 焊牢三千点是因为指数失真吗
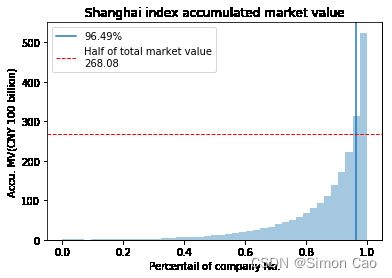
笔者认为不完全是,虽然笔者下面演示不同指数构建方式时,A股可能有让人出乎意料的表现,但A股不涨这件事和指数失真这件事并不存在必然的因果关系。上证指数是一个被大市值公司所绑架的指数,那么大市值公司造成的影响究竟有多大?笔者对上证指数成分股总市值进行了统计,按市值从小到大进行累计最后将数据输出到图一上。截至笔者撰文,上证指数共计2165支成分证券,总市值¥53.62万亿,其中80%的市值由仅3.51%的公司贡献:
图一:上证指数成分股累计市值(市值数据来源:Choice金融数据库)
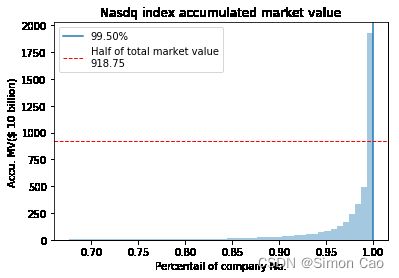
同样是市值加权的指数,纳斯达克指数4222支成分证券,总市值$18.37万亿,其中80%的市值由仅仅0.5%的公司贡献,如图二:
图二:Nasdq指数成分股累计市值(市值数据来源:Choice金融数据库)
两边一对比,纳斯达克指数的大市值偏差相对更加明显。但同样都是市值加权,谁会抱怨美股涨那么快,又有多少人会把美股涨那么快归结为使用了市值加权?拉出上证指数总市值前20家公司与纳斯达克指数前20家公司比一比(见附录),上证指数的顶流公司以银行和消费为主,而纳斯达克指数以科技企业为主,这个现象即使是放到A股和美股全市场也是存在的。为什么这些公司会从几千家公司中脱颖而出成为顶流?这些优秀企业不仅是一个指数的特点,更是国家优势行业,国家实力的体现,以储蓄消费,吃吃喝喝为主如何推动科技进步?如何提高全要素生产率?又如何诞生真正可以改变人类未来的伟大企业?笔者认为A股多年不涨的归根结底在于内生性因素,这是更值得所有人思考的问题,如果将其归结于指数失真无异于行掩耳盗铃之举。
2.3 A股指数构建方式是否合理
笔者认为合理性较高,指数构建是否合理应该从多方面进行综合考量,而不是部分投资者感叹失真它就不是一个好的构建方式了。 前面总结的各种构建方式优缺点中只有市值加权的优点是最为突出的,笔者认为“失真”只是部分投资者对一厢情愿的感慨。我们不得不承认金融市场的本质是为了实体企业融资提供便利的渠道和平台,帮助实体经济发展,而不是帮助股民低买高卖投机倒把,为了好看而做出一个绣花枕头一样的高指数没有任何意义。其次,在市场上还有很多被动跟踪指数的投资者,采用市值加权不管对于被动投资者还是指数编制者而言都是十分友好的方式。最后,市值加权体现了大市值公司股价稳定的特点,也屏蔽掉部分小市值公司的大波动,这有助于维护金融市场稳定性。当前的市场尚且有这么多人叫苦不迭,如果换成放大波动的其它构建方式那才对于A股投资者才是更糟糕的状况。
3. 上证指数重构
虽然笔者认为上证指数构建目前来说是合理的,但并不妨碍出于分析目的对指数构建方式进行调整。需要注意的是,一旦进行重构,会动摇很多分析框架得到的结果。例如计算市场风险溢价,在不同指数构建方式下回报率可以说是大相径庭,这直接影响到折现模型的计算结果。但进行指数重构仅仅只是帮助分析市场状态,寻找量化因子,构建投资策略等,如果硬要用自己重构出的特色指数套用进经典估值模型是很难被市场接受的。
3.1 重构原则
在对指数重构时,除了遵守第一节所阐述的构建原则,笔者对数据和统计范围做出如下规定:1)包含上海交易所所有历史数据,如退市公司数据;2)交易数据采用除权数据;3)统计区间为2004年1月2日至今;数据方面笔者选择Tushare金融数据库,省下很多写爬虫的时间,不过笔者下面所请求的数据需要2000积分方可调取(需要充值)。
3.2 代码实现
导入需要的模块:
import tushare as ts
import numpy as np
import pandas as pd
import os
import matplotlib.pyplot as plt实例化Tushare的接口:
key = "" # 输入自己的密钥
pro = ts.pro_api("key")由于需要反复计算不同指数构建方式,笔者选择先将成分股数据下载好然后之间从本地读取数据,先通过stock_basic获取上证交易所所有成分证券代码列表,这里需要包含已退市公司,参数list_status=“L”即表示正常上市的公司,“D”表示退市公司,“P”表示暂停交易,如果没有暂停交易的公司Tushare就会报错AttributeError。笔者请求的时候报错了,因此直接注释掉第三行代码:
lst = pro.stock_basic(exchange='SSE', list_status='L', fields='ts_code,name')
lst = lst.append(pro.stock_basic(exchange='SSE', list_status='D', fields='ts_code,name'))
# lst = lst.append(pro.stock_basic(exchange='SSE', list_status='P', fields='ts_code,name'))运行后变量lst便存储了所有上证指数成分证券代码的列表,展示如下:
ts_code name
0 600000.SH 浦发银行
1 600004.SH 白云机场
2 600006.SH 东风汽车
3 600007.SH 中国国贸
4 600008.SH 首创环保
... ... ...
85 601299.SH 中国北车(退)
86 601558.SH 退锐电(退)
87 603157.SH 退拉夏(退)
88 603996.SH 退中新(退)
89 T00018.SH 上港集箱(退)
2255 rows × 2 columns接下来通过pro.daily_basic接口请求交易数据并保存到本地,需要花一些时间:
fail = []
for i in lst["ts_codes"].values:
df = pro.daily_basic(ts_code=i, trade_date='', fields='')
df.to_csv("i+".csv")得到数据后只要依据不同构建方式进行计算即可,不过需要注意时间维度进行匹配,因此先请求上证交易数据,通过这个列表获取交易时间作为匹配标准:
index = pro.index_daily(ts_code='000001.SH', start_date='20040101', end_date='20221212')
table_pct = pd.DataFrame(index = index["trade_date"].astype("int")) # 涨跌幅表运行得table_pct, 这是一个空列表,只有trade_date作为列标签,这样做的好处是后面只需要在这个列表中不断加入成分股的涨跌幅表格,DataFrame会按照日期标签加入到table_pct中,没有相应日期的会显示为Nan值,超出表格日期范围的会直接drop掉:
print(table_pct)
trade_date
20221212
20221209
20221208
20221207
20221206
...
20040108
20040107
20040106
20040105
20040102
4603 rows × 0 columns下面只要读取下载好的本地成分证券数据,计算涨跌幅并不断存进大表格中即可:
codes = os.listdir("C:/Users/Administrator/Desktop/data_full")
for code in codes:
df = pd.read_csv(code) # 需要补全数据文件所在路径
df.index = df["trade_date"]
df["pct_chg"] = df["close"]/df["close"].shift(-1) - 1 # 计算日涨跌幅
table_pct[code] = df["pct_chg"]
print("第{}\r".format(codes.index(code)), end="")可以看的得到的是一个非常大的表格,其中行标签为日期,列标签为成分股:
600000.SH.csv 600001.SH.csv 600002.SH.csv 600003.SH.csv 600004.SH.csv 600005.SH.csv 600006.SH.csv 600007.SH.csv 600008.SH.csv 600009.SH.csv ... 688787.SH.csv 688788.SH.csv 688789.SH.csv 688793.SH.csv 688798.SH.csv 688799.SH.csv 688800.SH.csv 688819.SH.csv 688981.SH.csv 689009.SH.csv
trade_date
20221212 -0.008197 NaN NaN NaN 0.024151 NaN -0.022400 -0.018541 -0.013793 0.012187 ... 0.053238 0.025977 -0.021861 -0.023940 0.056053 0.048743 0.009178 0.011039 -0.004981 -0.016224
20221209 -0.008130 NaN NaN NaN -0.010975 NaN 0.003210 0.013784 -0.003436 0.006391 ... 0.036395 -0.000514 0.009621 -0.011184 0.093838 -0.073229 -0.013055 -0.035575 0.006205 -0.000295
20221208 0.005450 NaN NaN NaN 0.000000 NaN -0.006380 -0.008080 0.003448 0.012948 ... 0.001312 -0.022122 -0.019912 -0.083063 -0.018831 0.200000 -0.016508 -0.010534 -0.000477 -0.024173
20221207 -0.002717 NaN NaN NaN 0.007152 NaN 0.004808 -0.024848 0.000000 0.012939 ... 0.014943 -0.003008 -0.001385 0.017565 -0.023044 0.028161 -0.008745 -0.004604 0.000239 -0.013064
20221206 0.000000 NaN NaN NaN 0.027388 NaN 0.000000 0.005484 -0.006849 0.020253 ... -0.043312 -0.005731 0.000721 0.029912 0.017537 -0.016729 0.012004 -0.003822 0.013298 0.014990
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
20040108 0.006055 -0.011382 0.024938 0.006198 -0.005123 -0.006427 0.005222 0.017799 0.016575 0.017225 ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
20040107 0.017606 0.035354 0.021656 -0.004115 0.027368 0.016993 -0.022128 0.014778 0.023563 0.003842 ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
20040106 0.029918 -0.011647 -0.019975 0.012500 0.009564 0.014589 0.007719 -0.014563 -0.077391 -0.005731 ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
20040105 0.050476 NaN NaN 0.025641 0.044395 0.071023 0.007779 0.009804 0.036036 0.058645 ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
20040102 -0.002849 NaN NaN -0.002132 0.011223 0.021771 -0.066182 0.004926 -0.043103 -0.009018 ... NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
4603 rows × 2254 columns下面就简单了,如果是等权加权只需要构建个lambda函数将行数据取一个平均值即可:
table_pct["sum"] = table_pct.apply(lambda x:x.mean(), axis=1)新建的"sum"列即是等权加权的日涨跌幅,下面设置个初始点位数(这里设2004年1月2日开盘价为起始点位)将每日的点位计算出来并输出到图表上:
r_list = table_pct["sum"]
r_list = r_list[::-1] # 按时间正序排列
r_list.dropna(inplace=True)
v = index["open"].values[-1] # 大盘起始点位
values = [] # 每日收盘点位数
for i in r_list.values:
v = v * (1 + i)
values.append(v)
plt.figure(figsize=(16,5))
plt.plot(r_list.index.astype("str"), values)
plt.xticks(r_list.index[::250].astype("str"), rotation=90)
plt.show()1):等权加权指数
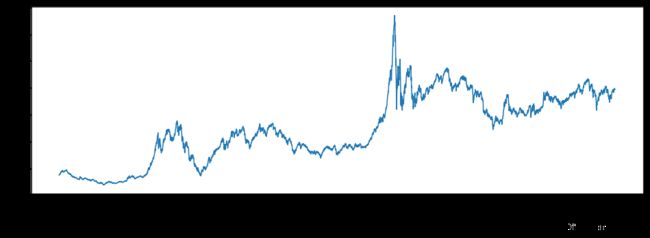
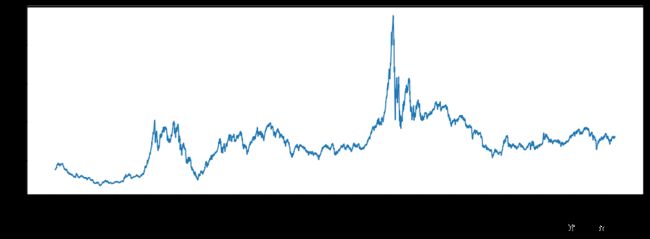
下面统一x轴为日期,y轴为点位数,运行上面代码得图三。如果以等权加权,笔者计算的上证点位数应该在将近8000点的位置:
图三:上证指数等权加权
下面还可以做基本面加权,如利用PE指标进行加权。需要注意的是Tushare将亏损公司PE统一设置为空值,也就是说笔者下面做的这个指数天然地剔除了亏损企业。由于需要计算涨跌幅前面乘的权重,笔者再创一个表用来记录PE数据:
table_pct = pd.DataFrame(index = index["trade_date"].astype("int")) # 涨跌幅表
table_pe = pd.DataFrame(index = index["trade_date"].astype("int")) # pe表
codes = os.listdir("C:/Users/Administrator/Desktop/data_full")
for code in codes:
df = pd.read_csv(code) # # 需要补全数据文件所在路径
df.index = df["trade_date"]
df["pct_chg"] = df["close"]/df["close"].shift(-1) - 1
table_pct[code] = df["pct_chg"] * (df["pe"])
table_pe[code] = df["pe"]
print("第{}\r".format(codes.index(code)), end="")下面就简单了,两张表按行加总然后相除即可得到PE加权的指数日涨跌幅:
table_pct["sum"] = table_pct.apply(lambda x:x.sum(), axis=1)
table_pe["sum"] = table_pe.apply(lambda x:x.sum(), axis=1)
r_list = table_pct["sum"]/table_pe["sum"]然后计算点位数,可视化输出得图四:
r_list = table_pct["sum"]/table_pe["sum"]
r_list.dropna(inplace=True)
r_list = r_list[::-1]
v = index["open"].values[-1]
values = []
for i in r_list.values:
v = v * (1 + i)
values.append(v)
plt.figure(figsize=(16,5))
plt.plot(r_list.index.astype("str"), values)
plt.xticks(r_list.index[::250].astype("str"), rotation=90)
plt.show()2):PE加权指数
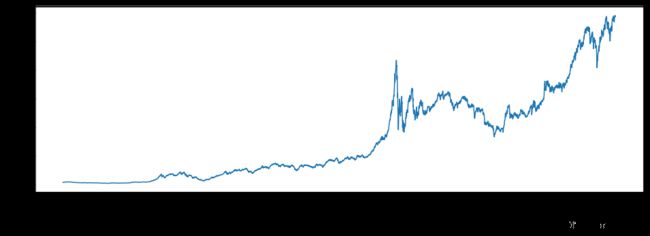
运行程序后PE加权竟然已经飙到快12万点了,笔者都有点不敢相信,检查一遍数据后发现数据没问题,如图四:
图四:上证指数PE加权
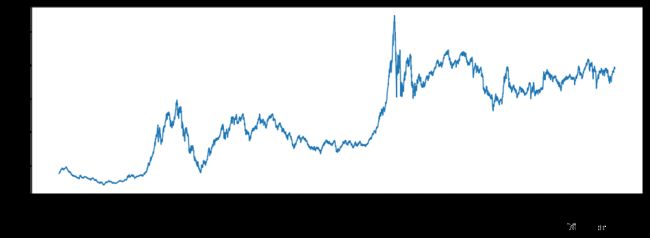
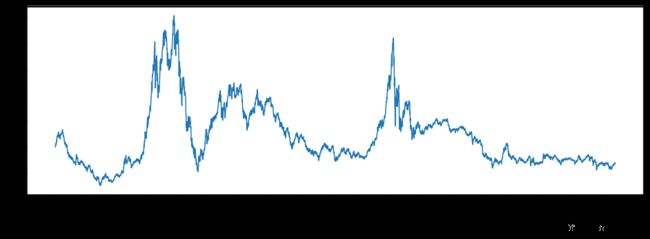
但笔者经过分析后认为采当天的涨跌幅采用当天的PE进行加权并不合理,数据正确但方法错了。这和等权加权是类似的道理,价格一直在变化,但我们起始是没办法让权重始终保持在最新的PE上的。其次,PE与每日涨跌幅有一定正相关关系,如果涨的越多,PE也会越高,这两个效果叠加在起来使得指数进一步不合理的推高。综上,笔者将代码修正为采用前一天的PE进行加权,得到图五。修正版的加权方式下当前上证点位为3000点左右,与目前上证点位非常相近:
图五:上证指数PE加权(修正)
3):PE反向加权指数
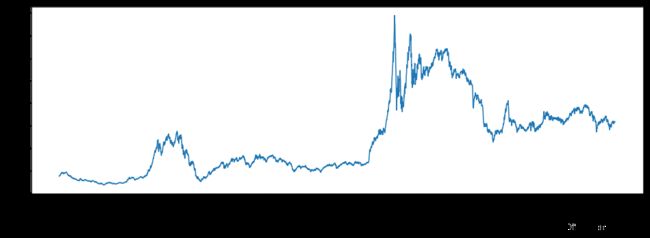
但对高PE公司进行超配并不是基本面投资者所奉行的准则,笔者不希望买入PE很高的公司,因此可以对上面的加权方式继续改造一下,加权时采用PE的倒数,笔者将之称为反向加权,可以得到图六:
图六:上证指数PE倒数加权(修正)
可以看到,以PE倒数进行加权当前的点位在8000点左右,这个指数反应的是低市盈率公司特点。笔者认为当前指数的估值水平虽然不高,但也并不算很低的位置,至少不是很多财经媒体所吹嘘的黄金坑。此外,与PE加权的指数进行对比还可以总结出一条规律:长期来看低市盈率公司跑赢高市盈率公司。
4):PB加权指数
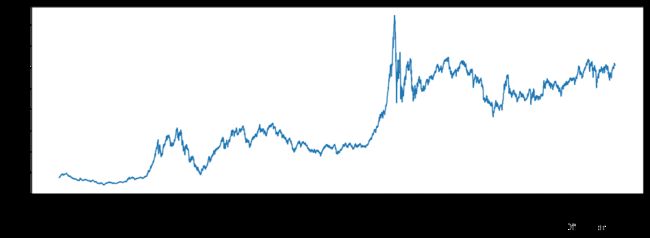
除了PE当然还可以对PB进行加权,这里处理方式与之前是一模一样的就不放代码了,下面笔者采用PB指标加权得到图七,目前点位来看在6000点:
图七:上证指数PB加权(修正)
同样可以采用PB倒数反向加权,目前点位在12000点,走势上也比PB指标加权更强,如图八:
图八:上证指数PB倒数加权(修正)
根据PB指标依然可以得出结论:长期来看低市净率公司跑赢高市净率公司。另外,PB所超配的公司强于PE,不过走势上是非常相似的,这很明显体现了价值股的特征。
5):防御型策略指数
笔者继续采用红利进行加权构建防御型的特色指数,得到图九:
图九:上证指数红利加权(修正)
可以看到,虽然超配高股息率的公司,但其走势是非常弱的,当前点位在1000点左右。
还有一些另类的加权方式,但需要自行进行调整和设置的参数更多,很难有什么统一的标准,笔者就不做演示了。
4. 未来展望
尽管A股才经历指数编制改革,但很难说未来还会不会出现新的改革。不管怎样改,一定是朝着促进金融市场有效性,维护金融市场稳定性的原则上改。从编制方式上看,笔者认为采用市值加权的基础是很难被动摇的,未来的改革基本只会在现有框架基础上进行微调,例如扩大风险警示股票的范围,进一步完善IPO和退市门槛等等。最后,笔者认为不管如何编制指数,决定一个指数强与弱的绝不是依靠指数编制方法改革,诞生更多真正可以改变人类未来的伟大的企业才是王道。
5. 附录
1):上证指数市值前20一览
| 代码 | 名称 | 总市值(¥亿) |
| 600519.SH | 贵州茅台 | 22,247.2630 |
| 601398.SH | 工商银行 | 15,147.2659 |
| 601288.SH | 农业银行 | 10,044.5127 |
| 601857.SH | 中国石油 | 9,114.4447 |
| 601628.SH | 中国人寿 | 10,282.7000 |
| 600036.SH | 招商银行 | 9,172.4576 |
| 601988.SH | 中国银行 | 9,214.3382 |
| 601318.SH | 中国平安 | 8,343.1021 |
| 600900.SH | 长江电力 | 4,641.6134 |
| 601088.SH | 中国神华 | 5,497.6195 |
| 601888.SH | 中国中免 | 4,620.3829 |
| 600028.SH | 中国石化 | 5,252.1291 |
| 603288.SH | 海天味业 | 3,733.4799 |
| 601166.SH | 兴业银行 | 3,583.5571 |
| 600809.SH | 山西汾酒 | 3,464.5204 |
| 601012.SH | 隆基绿能 | 3,073.6065 |
| 600309.SH | 万华化学 | 2,788.4089 |
| 600276.SH | 恒瑞医药 | 2,344.2833 |
| 600030.SH | 中信证券 | 2,932.9864 |
| 601668.SH | 中国建筑 | 2,272.8463 |
数据来源:Choice金融数据库
注:截至2022年12月24日
2):纳斯达克指数总市值前20一览
| 代码 | 名称 | 总市值($亿) |
| AAPL.O | 苹果 | 21,035.3038 |
| MSFT.O | 微软 | 17,755.8098 |
| AMZN.O | 亚马逊 | 8,547.9661 |
| GOOG.O | 谷歌-C | 6,151.7221 |
| GOOGL.O | 谷歌-A | 5,241.9049 |
| TSLA.O | 特斯拉 | 3,958.2426 |
| NVDA.O | 英伟达 | 3,819.4110 |
| META.O | Meta Platforms Inc-A | 3,105.4939 |
| PEP.O | 百事 | 2,494.8936 |
| AVGO.O | 博通 | 2,311.2866 |
| ASML.O | 阿斯麦 | 2,208.2334 |
| AZN.O | 阿斯利康(US ADR) | 2,109.8377 |
| COST.O | 开市客 | 2,035.9430 |
| CSCO.O | 思科 | 1,943.9544 |
| TMUS.O | T-Mobile US Inc | 1,735.9682 |
| ADBE.O | 奥多比 | 1,564.4814 |
| CMCSA.O | 康卡斯特 | 1,505.4109 |
| TXN.O | 德州仪器 | 1,494.7706 |
| HON.O | 霍尼韦尔(US) | 1,427.4073 |
| AMGN.O | 安进 | 1,415.3723 |
数据来源:Choice金融数据库
注:截至2022年12月24日