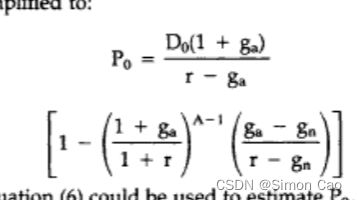浅谈估值模型:增速g的测算,H-model,可持续因子及周期因子
摘要及声明
1:本文主要介绍公司不同增速模式的计算方法,详细解释五种增长模式的运用,并以A股某上市公司为例简单实现一个带有可持续因子的折现模型;
2:本文主要为理念的讲解,模型也是笔者自建,文中假设与观点是基于笔者对模型及数据的一孔之见,若有不同见解欢迎随时留言交流;
3:笔者希望搭建出一套交易体系,原则是只做干货的分享。后续将更新更多内容,但工作学习之余的闲暇时间有限,更新速度慢还请谅解;
4:本文主要数据通过通过爬虫获取;
5:模型实现基于python3.8;
上期的估值模型讲解了折现率r的计算,本期将对折现模型中另一个重要的变量g(增速)进行讨论,在笔者看来,增速是折现模型中重要性仅次于折现率r的存在,也是一家公司未来景气度的直接体现。本文主要内容如下:
目录
1. 增速的估计
2. 常见的增长模式有哪些
3:两种不常见的增速模式
3.1 可持续因子
3.1.1 可持续因子的推导
3.1.2 持续增长是一种谜之信仰
3.2 周期因子
3.2.1 周期式演进
3.2.2 因子推导
4. 模型实现
4.1 电子表格建模
4.2 代码实现
5. 跳出模型
6. 参考文献
1. 增速的估计
所谓买股票就是买未来,增速的重要性不言而喻。笔者在第一期GGM模型中曾经讨论过永续增长率的四种计算方式:1)公式法;2)历史数据法;3)预测法;4)内幕消息法(最后这个当时有点开玩笑的意味),原文链接:浅谈估值模型:实现GGM的理想国。因为这篇文章基于GGM模型,当时讨论的增速是股利永续增长的概念。如果要说更广义一点的概念,增速除了是股利的增长,还可以是公司规模增长,市场份额的增长,主营业务增长,销售的增长。如果采用自上而下的分析,增速还是GDP的增长,市场规模的增长。
笔者将增速拓展到宏观经济就是希望在进行估值工作的时候不要只盯着股利折现公司和分红历史数据看,有些时候分红是不可靠的,不分红甚至乱分红的公司比比皆是。除了公司分红能力,公司业务能力,成本控制,行业竞争,以及宏观大势都会间接作用到公司分红上。难道能说疫情期间一家公司顶着外部压力拼命给股东分红,把股利折现公式的分子提高了就值得高估值?一家公司是一毛不拔的铁公鸡,就是不给股东分红就得低估值?显然这都不合理,因此需要在估值的时候还需要结合合理的估值方式然后至下而上的看给予的增速是否公允。
2. 常见的增长模式有哪些
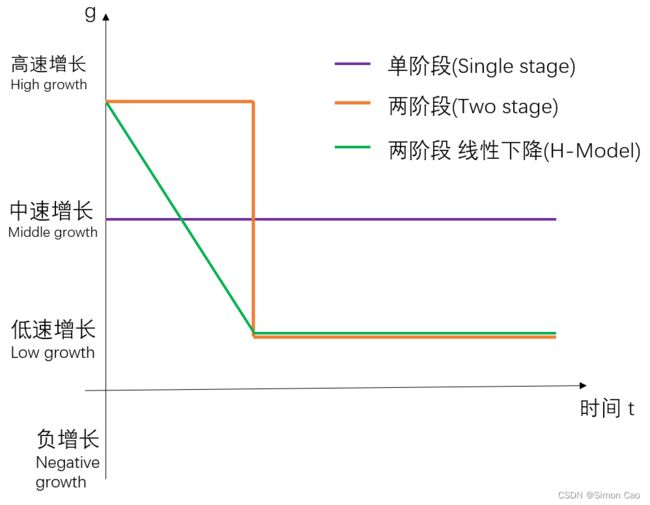
如图一,笔者将最常见的三种增长模型总结如下:
图一:常见的增速模式
以上几种模式算是很基础的模式,笔者处于内容的完整性还是写了一下。如果都学过可以直接跳过本部分看第三部分。
笔者用模拟生成了一些不同增速模式下的股利增长数据,笔者假设下一期股利![]() 为1.2元,折现率
为1.2元,折现率![]() 恒定为10%。
恒定为10%。
1):单阶段增长(图一紫线)
最经典的戈登增长模型,假设股利以某个固定的增速![]() 永续增长。设
永续增长。设![]() 为现值,计算公式为:
为现值,计算公式为:
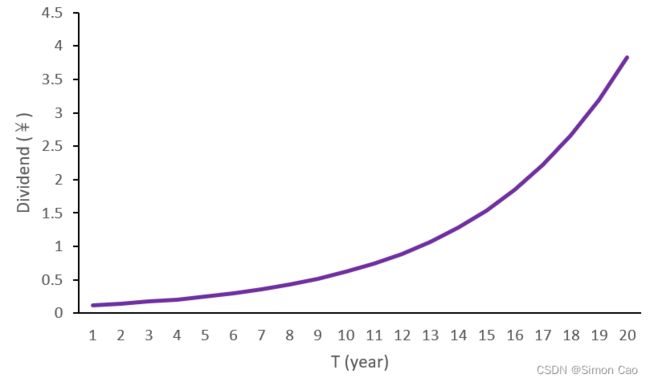
设定增速为20%,把股利的数值画下来就是条不断加速上翘的曲线。图二可以看到增长到第20期的股利为3.83元:
图二:单阶段增长(g=20%)
不过戈登增长假设股利以某个恒定的增速增长,而事实是很多公司处于生命周期的不同阶段,会经历多个不同的增长阶段。由此可衍生出几个多阶段模型。
2):一般两阶段增长(图一橙线)
一般两阶段假设股利在第一阶段以恒定速度增长,进入第二阶段时骤减至长期可持续增速。设当期股利![]() ,高增速为
,高增速为![]() ,低增速为
,低增速为![]() ,在第n期骤减至低增速,则计算公式为:
,在第n期骤减至低增速,则计算公式为:
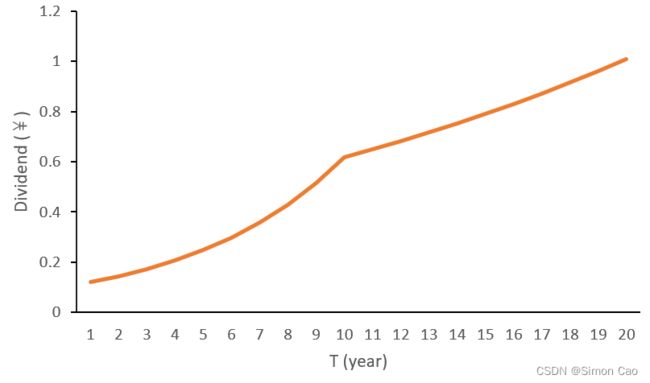
假设第10年从高增速(20%)直接过度到低增速(5%),图三可以看到斜率打了个折,后面第二阶段也是不断上翘的走势,但由于低增速导致第20年的股利降低至1.01元,在图二单阶段增速模式下则是4元左右,差距很大。
图三:一般两阶段增长(![]() =20%,
=20%,![]() =5%)
=5%)
以此为衍生的还有三阶段增长,n阶段增长,只是再两阶段基础上再加更多阶段而已,原理一样就不展示了。
3):H模型(图一绿线)
由于两阶段增长假设增速突然从高增长掉到低增长,这与现实是不相符的。H模型在增速过渡上进行了平滑处理,假设从高增速逐年递减到低增速。计算公式为:
其中,H为二分之一从![]() 向
向![]() 所需要的期数,假设从高增长过渡到低增长花了A年,那么H就等于A/2。笔者稍微介绍一下H模型是怎么来的,H模型最早是由两个学者(Russell & Chi-Cheng, 1984)【1】在1984年的论文”A simplified common stock valuation model“提出的。 如果稍微看下这篇论文就会发现公式[3]的推导其实是一种对平滑增速下的近似估计(为了更为简便的计算折现率r),该文章作者提供了精确计算式:
所需要的期数,假设从高增长过渡到低增长花了A年,那么H就等于A/2。笔者稍微介绍一下H模型是怎么来的,H模型最早是由两个学者(Russell & Chi-Cheng, 1984)【1】在1984年的论文”A simplified common stock valuation model“提出的。 如果稍微看下这篇论文就会发现公式[3]的推导其实是一种对平滑增速下的近似估计(为了更为简便的计算折现率r),该文章作者提供了精确计算式:
图四:H模型【1】的精确计算式,其中A为第一阶段的期数
图四H模型精确计算式的推导其实用几何级数,至于近似式[3]笔者认为则是用了点求面积的思想(公式[3]后半部分其实是求了个三角形面积的感觉),不过不是重点,需要原论文的可以留言。
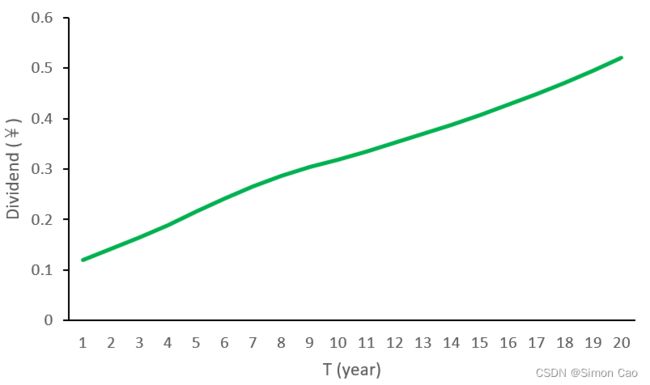
图四是经过H模型平滑的股利,看上去是一条直线,但其实是有一点扭曲的。在由高增速向低增速过渡的阶段股利是一条斜率不断变低的曲线(负凸度),而低增速阶段在经过很多期的增长后则是一条上翘的曲线。不过H模型平滑后第20期股利仅为0.52元,是两阶段模型的一半,差距也很大。不过值得注意的是笔者假设10年内下降到5%,如果是20年内缓慢下降到5%,H模型结果则会高于刚刚用一般两阶段增长计算的结果。
图五:H模型股利变化(![]() =20%,
=20%,![]() =5%,A=10)
=5%,A=10)
以此为衍生的还有三阶段H模型,甚至N阶段,原理是一样的,也不做过多演示。
3:两种不常见的增速模式
刚刚展示的几种增速模式应该是基本功,下面笔者介绍两种很少见的增速模式,一个是来自残余收益模型的可持续因子,另一个是笔者自己推导的周期因子。
3.1 可持续因子
不难发现之前的增长模式都有一个共同特点——未来很美好。高增也好,低增也好,总归是永续增长的。可实务中还有一种可能是行业在走下坡路,未来的股利可能不断减少,甚至整个行业消弭。一个残酷的现实是除了可口可乐这样的百年企业,更多的是昙花一现。谁也不敢保证十年后的某家公司是否还会存活,因此永续增长假设就变得不可靠。那么有没有假设现金流不断减少的增长模型呢?
3.1.1 可持续因子的推导
在残余收益模型中就引入了可持续因子,或者称之为衰减因子![]() 。残余收益模型笔者后面会出一期单独讲,不过本期先引入一下不断衰减的理念。可持续因子是基于现金流不断降低为前提假设,经典计算公式为[4]:
。残余收益模型笔者后面会出一期单独讲,不过本期先引入一下不断衰减的理念。可持续因子是基于现金流不断降低为前提假设,经典计算公式为[4]:
其中,![]() 为可持续因子,取值范围[0, 1]
为可持续因子,取值范围[0, 1]
该公式其实就是戈登增长模型演化而来的,如果令[1]式中的![]() 就可以将[4]式推导出来。根据所给条件不难发现
就可以将[4]式推导出来。根据所给条件不难发现![]() 的存在会使得增速
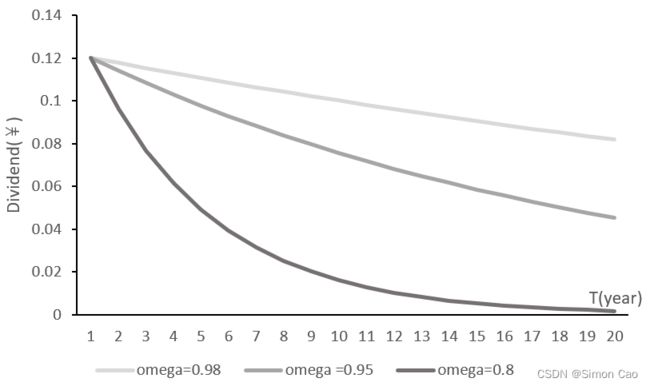
的存在会使得增速![]() 小于0,也就是说现金流非但没有持续上升,反而持续以负增速下降。如图六:
小于0,也就是说现金流非但没有持续上升,反而持续以负增速下降。如图六:
图六:不同衰减因子下的现金流变化
通过图六可以直观感受到持续因子的作用——持续力度。![]() 越接近1则表明持续力度越大,越接近0则持续力度越小,现金流会更快下降到0(但反过来想整个逻辑,
越接近1则表明持续力度越大,越接近0则持续力度越小,现金流会更快下降到0(但反过来想整个逻辑,![]() 就会变成衰减力度的概念,因此又可以称之为衰减因子)。如果结合一下之前的三种增速模式一样可以组合出多阶段的增速模型,而可持续因子模型可以放在最后一个阶段,即行业逐渐走下坡路,甚至最后企业破产,一分钱都没有了。
就会变成衰减力度的概念,因此又可以称之为衰减因子)。如果结合一下之前的三种增速模式一样可以组合出多阶段的增速模型,而可持续因子模型可以放在最后一个阶段,即行业逐渐走下坡路,甚至最后企业破产,一分钱都没有了。
3.1.2 持续增长是一种谜之信仰
既然加入可持续因子的模型更贴合实际为什么它还非常少见?
它终究是残余收益模型的因子,与绝大多数以股利折现为代表的模型理念相悖。笔者认为原因有三:
1):与永续经营假设相悖
虽然笔者还没对残余收益进行讲解,但是光听名字就知道了,残余残余,剩下来那种,是濒临破产的企业才会考虑的东西。这对于以戈登增长和永续经营假设为代表的模型来说简直就是完全相悖的理念。
2):与做多的逻辑相悖
既然假设企业股利一直下跌,到最后甚至破产,那么还买入这家公司的股票意义何在?用了这种方式去折现就陷入一种自我否定,这就好比是一根心头刺,让人不舒服。
3):与做空的逻辑相悖
换一个角度去想,残余收益其实提供的是一个地板价,再坏再坏大不了以后负增长直到企业破产了。这套逻辑是做多者寻求的安全边际或者说地板价,即再糟糕也不会比这个更糟了。而对于做空者这反而成为了一个天花板价。做空者更希望寻求的是戈登增长模型式的上限,即再好也不会比这个更好了,这样才能期待未来有更多下跌空间。
这样一个处处受气的因子,其适用范围自然就被限制在给走下坡路,未来看不到什么希望的行业和公司估值。不过反过来想,这个因子的确给做多者提供了一定的安全边际作为参考,前提是设置了合理的衰减力度![]() 。
。
3.2 周期因子
该因子完全是笔者自己闲来无事做的一些演算,由于这种折现的推导都很基础,笔者也不打算单独写一篇论文了。因此未经实证检验研究,也没有任何实践尝试,本部分的观点仅代表笔者个人的一孔之见。
3.2.1 周期式演进
对于很多行业来说都呈现周期式波动的特点,短则三年,长则十年,一般较常见的五年左右一个周期。但戈登增长也好,多阶段也好,可持续因子也好,其实都没有对这种周期波动进行任何讨论。还一个现实情况是利用这些这些模型估值的对象很多都是上市公司,成熟企业。这些企业往往已经是某个细分领域的龙头老大哥,有句老话说得好,瘦死的骆驼比马大。即使这些企业面临行业下降通道,难保未来会不会出现新的增长曲线然后有拉出一波漂亮的业绩。
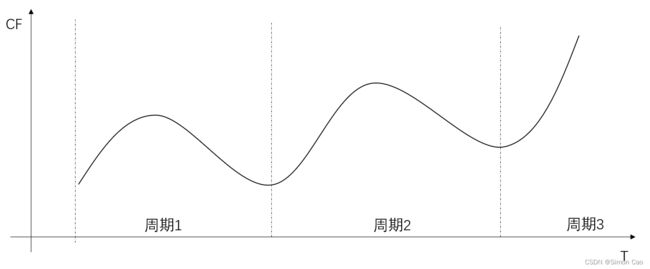
图七:现金流呈现周期性
3.2.2 因子推导
但想要将周期波动纳入折现模型是十分困难的,因为很多假设条件在便利于我们推导出简洁公式的同时也牺牲了一些实操性,以至于很多理念都是象牙塔上的理想化模型。笔者自行尝试将周期波动纳入折现模型中,这里笔者借用公司金融中的最小公倍数法化繁为简。
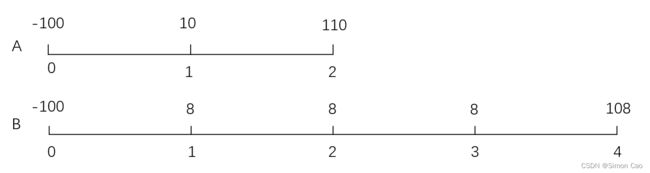
例如图七,现在有AB两个项目,一个2年,一个4年。对于不同时间长度的项目来说我们无法直接比较NPV和IRR这些指标,因此最小公倍数法采用延长这两个项目的现金流期限至最小公倍数年限。例如图七这个例子就可以延长A的年限至4年使之与B项目的四年可比。
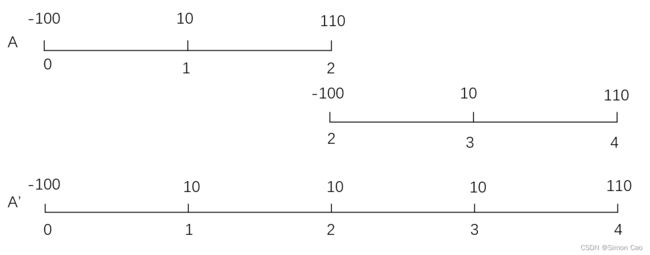
图九:延长A项目现金流使之与B项目可比
既然公司金融可以这样一段一段的现金流进行延长,现金流的周期式折现也是可以实现的。
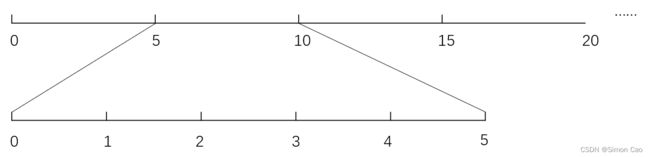
假设每个周期都是固定的五年,结合公司金融这种最小公倍数的操作,其实就可以只关注于预测一个周期,接着只要假设往后的所有周期都如此循环往复即可。
图十:大周期拆分
另设几个周期级别的因子:
![]() :大周期级别的年化增速
:大周期级别的年化增速
N:大周期个数
![]() :单个周期长度
:单个周期长度
先计算单个周期的现金流现值:
由于假设大周期级别增速为![]() ,可知第N个周期期初的现金流现值为
,可知第N个周期期初的现金流现值为![]()
那么现在的任务就转变成对大周期级别的折现,如图十一所示。
图十一:大周期级别的折现
根据现金流折现:
几何级数化简,两边同时乘以公比:
[5]-[6],化简得[7]式:
当然如果假设未来的周期完全一模一样,增速g的条件可以被删去并得到[8]式:
其实[7]和[8]还是种另类的戈登增长模型,只是该式将大周期内部的波动进行了计算,而并非戈登增长那样单期股利的永续增长。不过这个模型需要以下假设:1): 每个周期波动的年限相等;2): 折现率r是一个不变的常数,不会受到周期影响;3): [7]需满足周期间年化增速为g;4): [8]需满足周期间完全一致,没有增长。
4. 模型实现
4.1 电子表格建模
就是利用Excel,其实很多分析师都有自己的估值模板,输入相关参数直接就出结果了,并且”电子表格也是分析师协作共享的方式之一,增加了估值工作的便利性“(这句话笔者直接摘抄自以前的教科书,有点官样文章不过分析师用Excel的确实很多)。
4.2 代码实现
既然笔者是C站博主,自然不会展示什么Excel的操作,小红书上有很多Excel的例子。这里笔者打算写几个模块,把上面的几种折现方式全部实现出来,后面只要调用相关模块并传入参数就可以直接出结果了,并且笔者打算将之前的PSM折现率计算模型也内嵌进去。Excel的确很方便,但如果想内嵌一些非常复杂的模型还是不能偷懒,得自己写代码实现。
因为还要考虑到与其它模块协作,下面笔者为自己的七个增速模型创建了个对象,通过创建静态方法直接传参调用。创建对象好处在于还可以通过实例化直接调用属性和方法,为后面更多模块加入做准备。不过这是笔者的个人需求,当然也可以把这些模型全部写成普通函数调用。
# 下标沿用文章里的表达方式
class growth_mods():
@staticmethod
def ggm_mod(r, g, div): # 单阶段GGM
v = div*(1+g)/(r-g)
return v
@staticmethod
def two_ggm_mod(r, g_a, g_n, div, A): # 两阶段GGM
sum_div = 0
for i in range(A):
sum_div += (div*(1+g_a)**(i+1))/(1+r)**(i+1)
sum_div_terminal = ((div*(1+g_a)**A)*(1+g_n))/(r-g_n)
v = sum_div+sum_div_terminal/((1+r)**A)
return v
@staticmethod
def three_ggm_mod(r, g_a, g_n, g_l, div, A, B): # 三阶段GGM
sum_div_beg = 0
for i in range(A):
sum_div_beg += (div*(1+g_a)**(i+1))/(1+r)**(i+1)
sum_div_middle = 0
for i in range(B-A):
sum_div_middle += div*(1+g_a)**(A)*(1+g_n)**(i+1)
sum_div_terminal = ((div*(1+g_a)**A)*(1+g_n)**(B-A)*(1+g_l))/(r-g_l)
v = sum_div_beg + sum_div_middle/(1+r)**A + sum_div_terminal/(1+r)**B
return v
@staticmethod
def h_mod(r, g_a, g_n, div, A): # H模型
v = (div*(1+g_n) + div*(A/2)*(g_a-g_n))/(r-g_n)
return v
@staticmethod
def persistance_mod(r, g, w, div): # 持续因子模型
v = div*(1+g)/(1+r-w)
return v
@staticmethod
def two_stage_persistance_mod(r, g, w, div, A): # 两阶段持续因子模型
sum_div = 0
for i in range(A):
sum_div += (div*(1+g)**(i+1))/((1+r)**(i+1))
last_div = (div*(1+g)**A)
sum_div_terminal = last_div*(1+g)/(1+r-w)
v = sum_div + sum_div_terminal
return v
@staticmethod
def cyclical_mod(r, G, CFs, fi): # 周期因子模型
sum_cf = 0
for i in range(len(CFs)):
sum_cf += CFs[i]/(1+r)**(1+i)
v = (sum_cf*(1+r)**fi) / ((1+r)**fi - (1+g)**fi)
return v有模型后下一步就是选取数据啦,笔者准备先看看目标公司的历史分红情况。
先写个爬虫模块爬取新浪财经上的股票历史分红数据,顺便进行可视化输出:
def craw_dividend(company):
url = "http://vip.stock.finance.sina.com.cn/corp/go.php/vISSUE_ShareBonus/stockid/" \
+ str(company) + ".phtml"
table = pd.read_html(url, attrs={"id": "sharebonus_1"}, header=[2])
div_inform = pd.DataFrame(table[0][::-1])
year = []
div = []
div_hist = div_inform["派息(税前)(元)"]
for i in div_inform["公告日期"]:
# row = div_inform.loc[table["公告日期"] == i ].index
row = div_inform[(div_inform["公告日期"] == i)].index.tolist()
div.append(float(div_hist[row].values))
year.append(i.split("-")[0])
dataset = {"year": year, "dividend": div}
div_table = pd.DataFrame(data=dataset)
# 由于有的公司一年分好几次红,下面需要对相同年份的数据进行合并
rows_list = []
for i in div_table["year"]:
index = div_table[(div_table["year"] == i)].index.tolist()
rows_list.append(div_table[(div_table["year"] == i)].index.tolist()) if index not in rows_list else next
for rows in rows_list:
if len(rows) == 1:
continue
else:
total_div = 0
for row in range(1, len(rows)):
total_div = total_div + div_table["dividend"][rows[row]]
div_table.drop(rows[row], inplace=True)
div_table.loc[rows[0], "dividend"] = total_div + div_table["dividend"][rows[0]]
div_table.reset_index(drop=None, inplace=True)
plt.plot(div_table["year"], div_table["dividend"])
plt.xticks(div_table["year"],rotation=90)
plt.show()
return div_table传入目标公司的数字代码即可:
code = input("Code:")
div_table = craw_dividend(code)运行得:
图十二:目标公司历史分红数据
如图十二,可以看到与该公司股利增长模式较为符合的是戈登增长模型。但这是历史走势,该企业是老基建的细分龙头公司,最近几年业绩收缩严重。笔者去年曾看见有分析师做出业绩每年下跌5%还是10%的悲观预测。下面笔者也将利用可持续因子模型对它进行估测,看看地板价会是多少。
先利用PSM模型计算要求回报率r, 由于PSM代码很多,笔者这里就直接省略掉了,需要的可以看笔者的PSM那期文章(浅谈估值模型:回报率r的进阶玩法——Fama-French及PSM)。将PSM内嵌到增速模型中,运行得:
def PSM():
return r
Risk_free rate(1 year): 1.8280 %
GLS Regression Results
=======================================================================================
Dep. Variable: RP R-squared (uncentered): 0.451
Model: GLS Adj. R-squared (uncentered): 0.450
Method: Least Squares F-statistic: 581.8
Date: Wed, 30 Nov 2022 Prob (F-statistic): 0.00
Time: 19:25:21 Log-Likelihood: 7598.8
No. Observations: 2841 AIC: -1.519e+04
Df Residuals: 2837 BIC: -1.517e+04
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
RM 1.0699 0.049 21.698 0.000 0.973 1.167
SMB -15.7294 3.074 -5.116 0.000 -21.758 -9.701
HML 13.2859 3.128 4.247 0.000 7.152 19.420
LIQ 2.6250 0.867 3.027 0.002 0.925 4.325
==============================================================================
Omnibus: 300.395 Durbin-Watson: 1.956
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1051.259
Skew: 0.504 Prob(JB): 5.27e-229
Kurtosis: 5.804 Cond. No. 155.
==============================================================================
Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.
CAPM结果: 0.0485
PSM结果: 0.0619
可以看到,笔者的模型跑出来要求回报率![]() =6.19%, 从P-value可以看出模型中的四个因子在99%的置信水平下都为显著,解释力度超过45%,总的来说PSM非常适合于这家公司。
=6.19%, 从P-value可以看出模型中的四个因子在99%的置信水平下都为显著,解释力度超过45%,总的来说PSM非常适合于这家公司。
根据刚刚拿到的股利数据计算历史增速情况:
growth = []
for i in range(len(div_table["dividend"].values)-1):
if div_table["dividend"].values[i] == 0:
pass
else:
growth.append((div_table["dividend"].values[i+1]-div_table["dividend"].values[i])/div_table["dividend"].values[i])
print(growth)
print(np.mean(growth))
# [1.0,
0.30000000000000004,
-0.46153846153846156,
1.8571428571428574,
-1.0,
0.16666666666666666,
-0.14285714285714285,
0.16666666666666666,
-0.2857142857142857,
0.4,
0.8571428571428571,
-0.3384615384615385,
0.16279069767441864,
1.4,
0.4083333333333332,
0.183431952662722,
0.05999999999999996,
0.12264150943396233]
# 0.2697913951195587 运行得均值26.98%,直接高出折现率近4倍,这意味着分母带有![]() 的模型全都没有办法使用。但笔者本次想进行的是地板价的估计,采用持续因子模型则没有这方面的担忧。另外,在历史增速中有个两个很大的异常值,笔者打算去掉极端值后再计算均值:
的模型全都没有办法使用。但笔者本次想进行的是地板价的估计,采用持续因子模型则没有这方面的担忧。另外,在历史增速中有个两个很大的异常值,笔者打算去掉极端值后再计算均值:
growth.remove(max(growth))
growth.remove(min(growth))
np.mean(growth)
# 0.09994389093807486 计算得9.99%。笔者将这个数值作为第一阶段的正常增速,第二阶段以10%的速度衰减(![]() =0.9)。
=0.9)。
下面调用模型,传入计算参数:
折现率6.19%,第一阶段增速9.99%, 持续因子0.9,期初每股股利,第一阶段增长持续时间3年:
div_beg = div_table["dividend"].values[-1]/10
print(growth_mods.two_stage_persistance_mod(0.0619, 0.09994, 0.9, div_beg, 3))
# 29.18207999595649计算得内在价值29.18元,截止笔者发文当前天价格为28.59元,也就是说按照笔者的这种地板价估测当前价位拥有较高的安全边际。
当然还有更极端的情况,我们不妨做点压力测试,假设从明年开始该企业股利每年下降20%,于是可以采用单阶段的可持续因子模型:
print(growth_mods.persistance_mod(0.0619, 0.09994, 0.8, div_beg))
# 9.995636502481862计算得10元,也就是说最坏最坏的情况,假设该企业每年增速都降20%,大概率十年之后基本就快破产了,那么它折现出来的价值为10元,这是一个地板价。在企业质量有保证的情况下如果观察到市场上的价格比这个地板价还低,大概率会是一个价值洼地,这种价位进去的安全边际更高。
5. 跳出模型
以上讨论均是模型结果告诉笔者的,但这一系列的折现都是基于企业快破产还发股利为前提。一个更残酷的情况是企业濒临破产或是处于成长阶段分红很少,或者根本就没有任何分红。模型在计算的时候只会考虑那几个因子,因此在进行估值工作的时候一定要跳出模型框架,跳出假设结合实际情况进行判断。
对于可持续因子笔者将在后面的残余收益中进行更深入的讨论,残余收益是什么?可持续因子为什么更适合残余收益折现?这些问题笔者将在后面的文章中解答,您若不弃,我们风雨共济。
6. 参考文献
【1】:Russell F. & Chi-Cheng, H. (1984). A Simplified Common Stock Valuation Model. Financial Analysts Journal, 40(5), 49–56. https://doi.org/10.2469/faj.v40.n5.49
![V_{0}=\sum_{t=1}^{n}\frac{D_{0}(1+g_{a})^{t}}{(1+r)^{t}}+\frac{D_{0}(1+g_{a})^{n}(1+g_{n})}{(1+r)^{n}(r-g_{n})}\, \, [2]](http://img.e-com-net.com/image/info8/6da4b315f1a045788987606a49c2c753.gif)