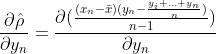金融危机模拟，开启灾难模式

摘要及声明

1：本文主要利用蒙特卡洛模拟金融危机，并进行模拟算法推导，笔者将利用模型简单实现一个模拟实验并分析危机爆发下的表现； 

2：本文主要为理念的讲解，模型也是笔者自建，文中假设与观点是基于笔者对模型及数据的一孔之见，若有不同见解欢迎随时留言交流；

3：笔者希望搭建出一套交易体系，原则是只做干货的分享。后续将更新更多内容，但工作学习之余的闲暇时间有限，更新速度慢还请谅解；

4：本文主要数据通过Tushare(ID：444829)金融大数据平台接口获取；

5：模型实现基于python3.8；

---

目录

1. 风险——复杂时代背景下的主旋律

2. 制造一场危机

3. 风险的重要特性

 4. 危机模拟

4.1 模拟方式

4.2 算法生成模拟涨跌幅

5. 模型实现

5.1 数据模拟模块

5.2 开启灾难模式

6. 模拟结果分析

7. 往期速览

---

1. 风险——复杂时代背景下的主旋律

        老话说得好，“以史为鉴可以知兴替”，这句话其实有很强的技术分析色彩，即相信规律，相信历史会重演。有很多人总结金融危机的原因并对金融系统进行一系列的改革和监管，巴塞尔协议就是很好的例子。从最初的巴塞尔协议到现在的巴塞尔协议3，促使巴塞尔协议每一次进行重大的修订的动力都是金融危机。可以明显感到监管在整个金融活动中所扮演的角色越来越重要，不过从巴塞尔协议的修订可见监管的滞后性。

        笔者认为历史分析的逻辑用在金融危机上有着捉襟见肘的一面，纵观历史，金融危机产生的原因多种多样，并且都蕴含着某个时间下独特的背景。我们很难利用这一场金融危机预测下一场会何时，亦或是以怎样的形式发生。笔者无意批判历史分析，八仙过海各显神通，没有所谓对错之分。只是笔者感觉金融危机进行预测是十分困难的，先不说很多数据我们拿不到，从格局上讲，普通人也很难有站在整个国家，乃至全球金融系统上看待风险的能力。比起预测，我们更多的只能被动承受危机。如今这个越来越复杂的时代，我们面临的潜在风险数不胜数，在以前我们单纯的认为大洋彼岸的次级贷款会引发金融危机，15年见识到杠杆的威力，18年又见识到贸易战对经济的冲击。当我们以为一切尽善尽美，还有病毒肆虐，地区冲突，等等。随着我们能探索的领域越广阔，人类自己就越发渺小，风险也将成为这个复杂时代下的主旋律，伴随这个时代成长。

2. 制造一场危机

        这里说得制造可不是在现实世界中制造危机，那笔者怕是要成全民公敌了。前面已经谈过危机的不可预见性，既然我们没办法预测危机何时发生，那何不自己制造一个类似沙盒那样的模拟。限制于能力笔者还做不到像数字孪生那样的庞大虚拟世界，一来要考虑的变量太多，二来技术所限。不过用蒙特卡洛模拟做一些靠谱的分析还是相当可行的，关注笔者的也会发现蒙特卡洛模拟是笔者十分钟爱的分析框架之一（具体笔者在技术分析中写过，想了解的也可以直接点击链接：股价预测模型 ）。

3. 风险的重要特性

        很多人以为风险分析简单，观察观察关键指标，没事在公司业务或者合规流程上找找茬完事儿。事实上风险涉及大量建模和量化，风险的特性也很难以几个简单指标表达。以较为看重风控的银行为例，很早以前的风险分析框架都是单向管道式的管理，行话也叫导弹发射井式管理（in silo）。它的理念是各个风控部门如同在一个个导弹发射井一样，各自管理各自对应的风险，职能差异导致它们老死不相往来。图一是笔者以前老师上课课件，因为是英文的，笔者按照课件自己画了一个，灵魂画手，比较简单，大概意思一样。

​

 图一：导弹发射井（in silo）式风险管理

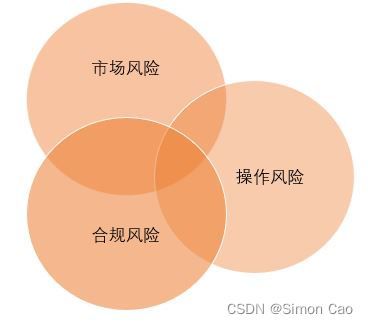
        在后面的操作中，人们发现，风险与风险之间并不是独立的，市场风险可能是公司合规问题造成，继而诱发合规风险，乌龙指这种操作风险又会导致市场风险，因此，在被市场教育之后，现代风险管理将风险与风险之间的相关性放在首位，并且将所有的风险统一划归到一个风险部门进行管理。

​

 图二：不同之间风险具有相关性

        风险之间的相关性也是近十年左右才被关注到，如果笔者的资料没错的话，最早一篇论文是Sandoval 和 Franca [1] 在2012中提到在极端事件发生时，市场倾向于“behave as one”。即是在极端情况下资产与资产之间的相关系数Rho会异常升高，甚至趋向于1 （想要论文原文的可以留言）。

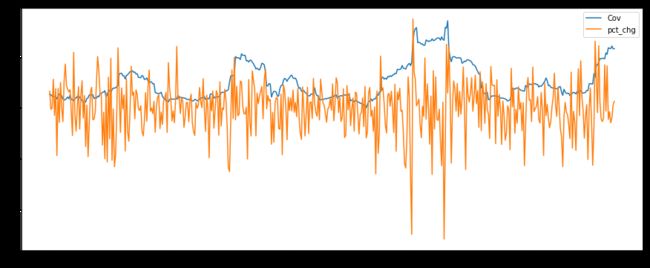
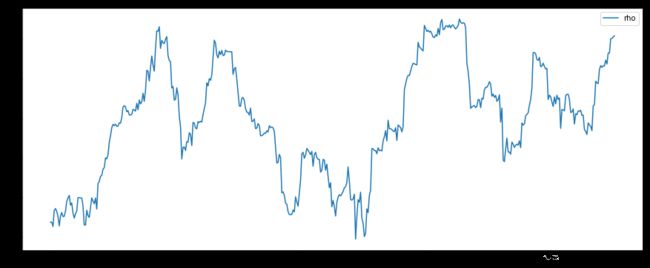
        笔者随便挑选了点数据展示一下，如图三、四，笔者选取上证指数及某证券2020年11月份到目前的收盘价及日涨跌幅，以30日为一个统计区间统计30天内的相关系数，并以日为单位进行窗口移动。对比两张图不难发现，在市场出现异常的时候，相关系数都会产生异常波动。这种波动在暴跌的时候异常明显，例如俄乌战争那段（x = 300)左右。

​

 图三：相关系数走势（蓝）及每日涨跌幅（橙）

​

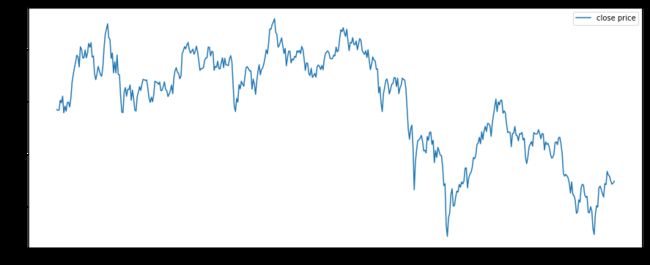
 图四：上证指数走势（收盘价）

        笔者顺带说一句，从走势上不难看出相关系数的不稳定性，而我们平时在进行绝对估值时使用的线性回归（例如CAPM计算r）都是建立在线性模型假设上，即数据要具有平稳性。平稳性的一个重要要求是序列​和其滞后期的协方差有限且恒定，统计后你会发现金融数据几乎不存在持久的稳定性，但我们还是硬着头皮用，用了半个世纪。谈到Rho顺带提一下，值得思考，不过不是重点。

 4. 危机模拟

        下面的部分就要带上数学推导了，不感兴趣的可以跳过，再下一个部分就是代码实现，对数学和代码都不感兴趣的可以看到这里为止。

4.1 模拟方式

        在知道风险的特性之后其实为我们模拟金融危机提供了一个思路，根据大盘的涨跌对个股可能做出的反应进行模拟。也就是说给定的是大盘的涨跌，我们需要依据大盘涨跌模拟出个股走势。

        大盘数据方面可以根据自己的判断采用模拟大盘数据进行计算，这种方式产生的数据独一无二，需要做很多假设。由于分析假设条件要花很多篇幅，笔者不选这种方法。第二可以依据大盘出现暴跌的历史数据进行历史模拟，笔者下面实现的就是历史模拟。一来直接结合历史情景更加真实，相当于重演一遍危机爆发时的惨烈。二来完全不需要什么假设，更加简洁。

4.2 算法生成模拟涨跌幅

        根据危机爆发时的相关系数进行模拟。这里需要解决的技术难点是在给定相关系数下，我们如何依据大盘涨跌数据模拟出个股走势。

        下面设大盘涨跌幅​， 个股模拟数据​， 在数列y中加入一个数​， 使得数列​和​之间的相关系数等于给定的相关系数​，问：​等于多少。

         笔者的解决思路是利用神经网络的那套误差下降算法让模型自己拟合出符合给定相关系数的走势，算法思路可以参考笔者的文章：浅谈股价预测模型：全能大明星——神经网络模型。

        根据相关系数公式：

​

        给定​可得相关系数：

​

       按理来说标准差里也有个y， 应该在推导时候求出来。但笔者推到后面发现相关系数公式的分母很是麻烦，干脆将标准差直接当成两个常数乘到相关系数上，把目标函数变成两个协方差的MSE。还有一个重要理由是涨跌幅设有限制，即使没有标准差约束数据也不至于出现量级上的偏差。这算是有点偷懒的做法，后面程序跑起来误差下降还是很顺，索性就把标准差当成已知常数处理了。有能求解出来的别忘了带笔者交流一下。

        设误差函数：

        链式法则求解​对函数​的误差：

​

        用协方差来展开第二部分：

        2,3式整理后合并进1式：

        接下来就是梯度下降算法的基本操作了，设误差为​，学习率为​，则​满足4式：

        得到误差后根据误差更新​：

        推导完成，还是比较简洁的，比起神经网络那套误差反传机制的推导友好很多了。

5. 模型实现

        有数学模型后笔者利用代码进行实现，数据方面笔者选择了Tushare金融大数据平台。Tushare非常简单好用，注册送的200积分即可请求很多经常使用的数据。前段时间双十一双倍积分活动笔者充了200得4000积分，一下子开了好多数据请求权限。想想万德choice几千上万的年费真是又便宜又香，不是打广告，真心觉得不错。

        笔者选用2015年股灾时候的大盘数据，随便选了一支个股与大盘在俄乌战争那段时间(2022年3月3日至4月27日)的相关系数当作是危机时的相关系数。笔者认为选取最近的相关系数是更有意义的，提高了估计的准确性。如果我们要模拟今年的，却选择了15年的相关系数，一来这么多年过去，公司的股性可能出现很大变化，二来用15年的大盘和15年的相关系数，大概率我们会模拟出来的还是15年的历史走势，与其这样我不如去看15年的历史走势不是更简单明了？参考意义不大。不过模拟08年危机的也是可以的，总之也是要分情况看。

5.1 数据模拟模块

        导入相关模块，因为numpy的协方差矩阵一下生成4个数，笔者不太喜欢，于是自己构建一个统计计算模块，协方差相关系数一起输出，方便：

import tushare as ts
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

pro = ts.pro_api(token) # 输入自己的API密钥


def rho_mod(x, y):
    cov = 0
    for i in range(len(x)):
        cov += (x[i]-np.mean(x))*(y[i]-np.mean(y))
    cov = cov/(len(x)-1)
    rho = cov / (np.std(x)*np.std(y))
    return cov # ， rho

        根据算法构建一个模拟股价生成模块：

def data_generation_mod(x, y, cov, η): # 给定协方差 根据x 生成相关y
    for days in range(1,len(x)-len(y)+1):
        y_n = 0
        y.append(y_n)
        partial_x = x[:len(y)]
        
        result = []
        for i in range(100):
            random_cov = cov_mod(partial_x, y)
            if abs(random_cov-cov) > 0.01:
                error = η * 2 * (random_cov - cov)*(partial_x[-1]-np.mean(x))/len(y)
                y_n -= error
                y[-1] = y_n
                result.append(abs(error))
            else:
                break
    return y, result

        下面请求数据：

code = "code" # 证券代码
index = pro.index_daily(ts_code='000001.SH', start_date='20220303', end_date='20220427')
stock = pro.daily(ts_code=code, start_date='20220303', end_date='20220427')

cov, rho = cov_mod(index["pct_chg"].values, stock["pct_chg"].values) # 要取消之前模块的注释
print(cov)

# cov = 3.1248296815090084 rho = 0.7783215483885252

        把cov_mod模块的rho注释取消掉可以看到相关系数为0.778，笔者挑选的股票属于β系数较低那种，0.778对于这支票来说相当高的了。笔者可以输出一下近两年的相关系数走势，以50天为一个统计区间，可以从图五看到，0.7几的相关系数已经是近两年最高了：

​

  图五：目标公司2020年-2022年历史相关系数走势

        接下来就简单了，请求股灾时候的数据，然后把数据抛给模拟模块计算：

η=0.6
cov = cov_mod(index["pct_chg"].values, stock["pct_chg"].values)
benchmark = pro.index_daily(ts_code='000001.SH', start_date='20150615', end_date='20150827')[::-1] 
simulate_data = list(stock["pct_chg"][:2].values) # 用前两个数当作种子

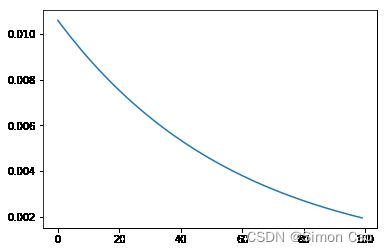
y , error= data_generation_mod(list(benchmark["pct_chg"].values), simulate_data, cov, η)

        简单查看一下误差收敛情况，由于函数非常简单，下降过程也很漂亮：

​图六：某次拟合的误差收敛情况

        查看真实协方差与模拟数据的协方差：

print("目标协方差:",cov, "拟合协方差：",cov_mod(list(benchmark["pct_chg"]), y))

# 目标协方差: 3.1248296815090093 拟合协方差： 3.1112561565213572

        可以看到，这次的收敛已经达到笔者规定的阈值0.01， 因为笔者只规定了100次的下降上限，如果想要更精确可以降低学习率，阈值，然后提高上限次数。但这种误差是完全可以接受的，因为笔者后面还有大杀器。

5.2 开启灾难模式

        模拟需要一个分布假设，笔者首先想到的是利用Bootstrapping重复计算得到一个估计区间，最开始用了随机取数，后来才发现不对劲，因为协方差对数据的分布敏感，那种有放回的随机取数会使得协方差估计有偏。于是笔者退而求其次，只取一个随机取数，然后选择该数后20个数组成数组。下面笔者利用Bootstrapping的方式构建2022年3月3日至4月27日的相关系数区间估计：

import random 
import seaborn as sns


def bootstrap_mod(x, y):
    dist = []
    for i in range(10000):
        a = random.randint(20, len(x))
        cov = cov_mod(index["pct_chg"].values[a-20:a], stock["pct_chg"].values[a-20:a])
        dist.append(cov)
    return dist


dist = bootstrap_mod(index, stock)
sns.distplot(dist)
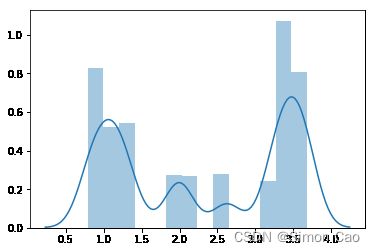
plt.show()

        得到的是一个不规则分布：

​ 图七：10000万次Bootstrapping

        最后就简单了，在这个分布中随机选协方差，然后传入模拟生成数据模块。下面进行100次模拟，因为引入了算法模拟模块，生成数据的速度变得有些慢，100次模拟不开多线程需要5分钟左右：

index = pro.index_daily(ts_code='000001.SH', start_date='20220304', end_date='20220427')[::-1]
stock = pro.daily(ts_code=code, start_date='20220304', end_date='20220427')[::-1]

simulates = []
η=0.6
benchmark = pro.index_daily(ts_code='000001.SH', start_date='20150615', end_date='20150827')[::-1] 
for times in range(100):
    simulate_data = list(stock["pct_chg"][:2].values) # 用前两个数当作种子
    y = data_generation_mod(list(benchmark["pct_chg"].values), simulate_data, dist[random.randint(0,len(dist)-1)], η)
    simulates.append(y)


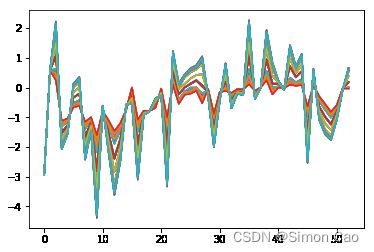
for i in range(len(simulates)):
    plt.plot(range(len(simulates[i])),simulates[i])
plt.show()

        运行得：

​图八：模拟回报率走势

        转换成价格走势：

price_simu = []
end_dis = []
for i in range(len(simulates)):
    value = 1
    v_data = []
    for r in simulates[i]:
        value = (1+r/100)*value
        v_data.append(value)
    end_dis.append(value) # 最后一天价格
    price_simu.append(v_data)

for i in range(len(simulates)):
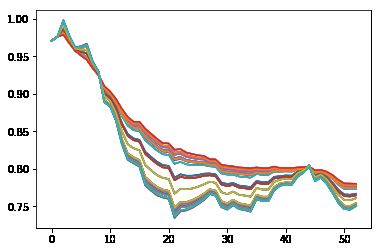
    plt.plot(range(len(price_simu[i])),price_simu[i])
plt.show()

# 最后一天的分布
for i in range(len(simulates)):
    plt.plot(range(len(price_simu[i])),price_simu[i])
plt.show()

import seaborn as sns
sns.distplot(end_dis)
plt.vlines(np.mean(end_dis), 0, 100, colors='b', linestyles='dashed', label="mean")
plt.legend()
plt.show()

print(np.mean(end_))
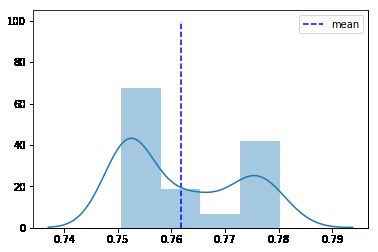
# 0.761889457142263

 图九：价格走势

 图九：最后一天的价格分布

6. 模拟结果分析

        从图八不难看出，暴跌的前20天是最惨的，下跌约20%左右，后面趋于平缓，而且稍微反弹了一下。这支股票在2015年模拟区间内真实的下跌幅度是近50%，但这是可以理解的，因为笔者想要模拟的是俄乌战争这段时间的相关系数，我们没有理由期望在三千点反复横跳的A股再向下走50%吧，因此笔者认为这次模拟是公允且成功的。

        覆巢之下安有完卵，危机之下反正都是跌，模拟出来的结果还是跌，这样的模拟有必要吗？笔者认为十分有必要，笔者这里只是简单对一支证券进行模拟，事实上，通过组合投资，大类资产配置是有可能对冲掉下跌风险的，它给我们的组合管理和日常交易提供一个压力景况下的表现，让我们更好的评估组合是否有能力吸收这样风险冲击的能力。

        另一点，利用Bootstrapping来形成协方差分布然后进行模拟是不太合理的，之前笔者讨论过资产的相关性是一直在变化的，而在传入模拟模块的协方差是个恒定的值。不过由于模拟区间才2个月，一来笔者认为变化不大，二来这只是进行了单个证券的模拟，采取比较简单的方式也不会对结果造成很大影响。但如果是模拟一年的数据，十几支成分证券，那需要考虑的东西就更多了。如果在加入其它大类资产，例如股票，基金，债券和房地产，情况又会变得非常复杂。写太多显得冗杂，这篇文章就浅尝一下，后续如果有需要笔者再对更复杂的情况进行分析。

7. 往期速览

往期速览
系列	子类别	文章传送门	实现方式
基本面分析	绝对估值	实现GGM的理想国	Python
		Fama-French及PSM	Python
	相对估值	PE指标平滑	Python
		PE Band	Python
技术分析	/	分类树算法	R
	/	蒙特卡洛模拟	Python
	/	全连接神经网络模型	Python
财务分析	财务建模	利润表	R
金融数据获取	/	多线程爬取	Python
	/	多进程爬取	Python
	/	selenium模拟网页爬虫	Python
其它	/	市场风险分析	Python
	/	金融危机模拟(本文)	Python

        虽然笔者在以前的文章中都多多少少会谈到风险，但这还是第一篇真正意义上以风险和相关理念为主题的文章。因为后面笔者攒几篇文章后打算再分个组合管理的系列出来，毕竟组合管理，风险先行。

        其实之前的文章，估值也好，预测也好，全是为了这个系列做的铺垫，属于是基本功。不过再加上这个系列的话笔者就开了四个系列了，散得太开单个系列的更新速度就会比较慢。笔者感觉老盯着一两个系列写太过枯燥，时不时换换分析思路和框架还是不错的。

参考文献：

[1]: Sandoval, Leonidas, & Franca, Italo De Paula. (2012). Correlation of financial markets in times of crisis. Physica A, 391(1-2), 187–208. https://doi.org/10.1016/j.physa.2011.07.023