Fast Odometry and Scene Flow from RGB-D Cameras based on Geometric Clustering 论文笔记

Fast Odometry and Scene Flow from RGB-D Cameras based on Geometric Clustering 论文笔记

摘要

主要思想是对场景进行两次分割，将其划分为几何聚类，这些几何聚类又被归类为静态或移动元素。

系统总览

输入颜色-深度图像对

首先，每一帧对场景点的3D坐标执行k-means聚类算法，分割成N个几何聚类。每一个聚类被视为一个刚体，

每个聚类的速度用twist ξi ∈ se(3) 来表示，里程计ξR ∈ se(3)的初始估计通过在稳健的M-估计器内最小化光度和几何残差来计算。

随后，这个估计被用于第二次分割，将场景分割为静态部分(或背景)和移动物体

根据ξR对I-D图像进行了变换，并计算了每个聚类的平均残差。属于静态背景的聚类根据ξR移动的残差较低，

一旦分割是已知的，它可以用来将运动估计过程分解为两个独立的步骤。

• 首先，使用所有被标记为背景的集群来获得更精确的ξO，现在不包括非静态部分。
• 其次，对场景的其余部分估计分割刚体场景流，假设每个集群表现为刚体。最后，使用新的优化的里程计重新计算背景分割，并将其变换到下一帧，得到BT: Ω→[0,1]。由于移动的物体可能会移动不止一帧，静止的部分也一样，我们在下一个迭代中使用B.T()来获得随时间一致的分割。

几何聚类

参考[Motion Cooperation: Smooth piece-wise rigid scene flow from RGB-D images]基于观测点的3D坐标计算K-均值聚类。

首先，我们构建一个连通性图G = {Gij, i = 1，…， N, j = 1，…， N}表示哪些聚类在空间上是连续的(Gij = 1)，

此外，我们对相邻的聚类进行了平滑处理，以避免沿其边界的剧烈运动过渡，但这种平滑主要影响场景流估计，而对我们算法的其他模块没有任何作用。

里程计

直接法通过最小化连续RGB-D图像对之间的光度ri和几何残差rz来计算位姿

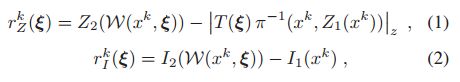
xk表示图像中的每一个给定像素 这两个也是直接法求取位姿的经典公式。

几何误差也就是深度误差，用位姿变换之后的2d像素点的坐标读取深度图2中的深度值减去3D点坐标变换得到的Z值。

T(ξ)∈SE(3)是与位姿变换ξ相关的齐次变换。其变换函数为:

构建成优化问题来获得相机运动，并计算残差的柯西m估计:

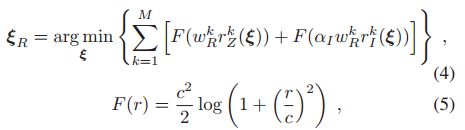
其中M是Z1中深度为非空的像素个数。参数αI对光度项和几何项进行加权。参数c标志着F的拐点，并且可以调整以使得估计对高残差或多或少的鲁棒性。

此外，应用预加权(wR)来帮助求解器收敛到真实的相机运动:

预加权主要是对两类点，一类是先验动态目标点，让其权重降低。另一类是远处点，提高其权重，因为更有可能是静态背景。

由于(4)是高度非线性的，运动在粗到细的方案中求解，线性化图像金字塔的每一级的残差，如[1]，[3]中所做的那样。在每一层，(4)的解通过迭代重加权最小二乘得到。

背景分割

为了背景分割，使用里程计获得的ξR来检查哪些区域/集群遵循这种运动模式。这种评估不是按像素执行的，而是按聚类执行的，因为我们假设聚类中的所有像素都具有相同的刚体运动。

首先根据位姿ξR对RGB-D帧进行变换。

经过变换后，属于背景的集群将具有较低的光度和几何残差，而与移动物体相关的残差仍然很高。

理论上，这个标准应该足以将场景分割为静态和非静态部分，但在实践中，这个过程要复杂得多，因为残差并不总是一个很好的度量来评估精确的图像对齐。

为了解决这些问题，本文将背景分割分为两个步骤。

首先，我们计算每个聚类残差(δ)的稳健度量。

其次，我们制定了一个最小化问题，根据它们的平均残差，它们的几何形状和它们之前的分割BT (每个聚类的BT (x)通过均值来计算，这里的BT可以视为根据上一帧的结果对当前运动判断的一个先验值)来获得聚类b的分割。

稳健平均残差计算为：

其中Si是第i个聚类的大小，Oi是聚类中被遮挡的像素的数量(不包括δi的计算)，Zi是聚类的平均深度。被遮挡像素被认为是几何残差低于某一阈值的像素，即像素x被遮挡的条件为：

接下来，我们制定了一个最小化问题，以获得背景分割。要最小化的能量函数由四项组成:

其中b是唯一未知的(与δ， bT和Z的依赖关系被清晰地显示出来)

当残差较低时，数据项ED将集群作为背景分割，反之亦然。为此，我们需要定义δ和b之间的映射，并指定低残差和高残差的阈值(分别为δL和δH)。为了简单起见，我们使用以下分段线性函数:

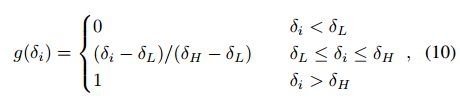
数据项ED就可以表示为：

其中

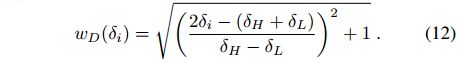
当残差远离不确定区域(δL < δi < δH)时，函数wD(δi)增加了数据项的权重，使明显是背景的一部分或移动物体的聚类具有更强的强度。

正则化项ER试图迫使邻近的集群获得类似的分割，并定义为

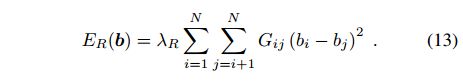
我们选择最小化(13)中的二次项，因为它有助于平滑带有误导性残差的聚类的偶尔错误标记。我们还尝试最小化差异的绝对值(总变量)，这允许连接的集群之间出现明显的不连续，但它没有提供更好的结果。

时间正则化(ET)也被施加，因为场景的静态和动态部分都很可能在时间中保持静止和移动(分别):

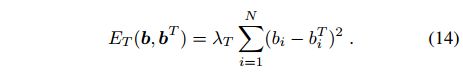
最后，我们包括一个额外的项，为所有远离相机的集群引入一个对背景的偏向(bi→0)。这模拟了这样一个事实，即在室内场景中，移动的物体往往在前景，而远处的观察可能会捕捉到环境的固定元素(墙壁、天花板、地板、家具等)。

场景流估计和里程计优化

一旦场景被分割，我们将运动估计分为两个独立的过程。所有作为背景分割的集群将被视为一个单一的刚性块，并用于重新估计里程。另一方面，独立计算移动簇ξi的刚体运动。已知ξi，计算集群i中每个点p(x)所关联的场景流s(x)为

由于b在[0,1]范围内是连续的，所以我们需要在该范围内创建一个分区来分离静态对象和移动对象。

我们没有在0.5处施加简单的二进制阈值，而是考虑以下三个区域:

• 如果bi < 1/3，簇i被认为是静态的，仅用于里程计估计。

• 如果bi > 2/3，则假设集群i是移动的，仅用于场景流估计。

• 如果1/3 < bi < 2/3，簇i的状态是不确定的，因此它被用于里程计和场景流估计

通过这种方式，没有被明确分割的集群贡献了里程估计(因为它们可能是背景)，但我们也计算了它们自己的独立运动。

通过最小化下面的误差，得到运动聚类的刚性运动

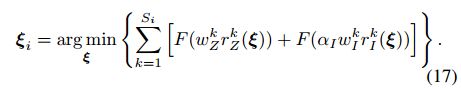
最终的里程计ξO的计算方法类似于最小化背景像素的(17)。这些优化问题几乎与第五节中描述的问题相同;唯一的区别是预加权策略。一旦场景被分割，我们使用预权重来惩罚遮挡和不连续，在优化过程中倾向于平滑区域，以找到精确的解决方案：

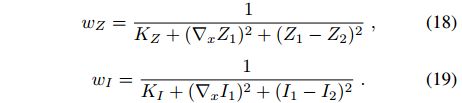
权重wZ和wI惩罚空间或时间梯度高的像素。虽然我们在论文中没有提供明确的比较，但这种预加权策略比没有预加权的纯鲁棒最小化提供了更好的结果，并且还有助于IRLS求解器在更少的迭代中收敛。

实现细节

柯西m估计器的参数设置

另一个重要方面是分割阶段δL和δH参数的选择。为了获得它们，我们计算了与聚类相关的稳健残差(δ)的中位数。由于移动物体群的残差通常会大大高于δ，所以我们将这个值设置为阈值。我们还观察到，平均残差随着相机的运动而增长，因此，我们还使δL和δH依赖于相机运动的范数:

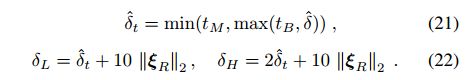
其余部分的参数设置如下：

• αI设置为0.15，使光度和几何残差贡献相等。
• 遮挡阈值(ΔZocc)设置为0.2米，背景分割中几何先验的ZMin设置为场景的平均深度除以4。
• 在分割阶段，将不同项的权重设置为λR = 0.5， λT = 1.5， λZ = 0.15。
• (18)和(19)中的预权重常数设置为KI = 0.1, KZ = 10−4。