数字图像处理第三次作业——基于直方图的图像空域操作

一、基本概念及原理：

1. 图像的直方图：

  我们常说的直方图是指频率分布直方图，即横坐标表示变量，纵坐标表示对每个变量取值的频率大小。在数字图像中，图像的直方图与之类似，横坐标是离散的灰度值，纵坐标是每个灰度值对应的像素点数目。

  所以直方图可以显示图像的明暗情况。越亮的图片直方图分布越靠右侧，越暗的图片直方图分布就越靠左侧；对比度越高的图片直方图分布越广，反之其分布较窄。

2. 直方图均衡：

  如上所述，对于对比度较小的图片，我们通过对空域的数学操作使其灰度在一定范围内的像素数目大致相等，这个过程就是直方图均衡化。直观来讲，就是将不均匀的直方图调整的更加均匀。 这样处理往往能使对比度小、不易辨识的图片更加清楚。

  我们通常用如下函数进行直方图均衡化：

$$S_k=T(r_k)=\sum _{i=0}^{k-1}\frac{n_i}{n}$$

  其中，$n$ 表示图像中像素总数，$n_i$表示图像中灰度为 $i$ 的像素点数量

3. 直方图匹配：

  所谓直方图匹配，就是将待处理图像的直方图调整成目标图像直方图的样式，这样做可以实现图像色调的统一。

  实现步骤：

1. 计算输入图像的均衡化直方图T(r)
2. 计算模板图像的均衡化直方图G(z)
3. 对于每个像素点的灰度r，找出使得T(r)=G(z)的z，若不存在则找最接近的，若有多个z值，则找最小的
4. 将r依次替换为z

4.局部直方图增强：

  所谓局部直方图增强，就是将图像中满足条件的像素点灰度增强。这个条件判断方式有多种，按照课本上的判断条件即是：

$$\{\begin{array}{llccc}g(x,y)=E\cdot f(x,y)& if& m_{S_{x}y}\le k_0{m}_G& AND& k_1{\sigma }_G\le {\sigma }_{S_{x}y}\le k_2{\sigma }_G\\ g(x,y)=f(x,y)& else& & & \end{array}$$

  其中，$m_{S_{xy}}$是邻域中的灰度均值，$m_G$是全图的灰度均值；${\sigma }_{S_{xy}}$是邻域中的灰度标准差，${\sigma }_G$是全图的灰度标准差。E，k0，k1，k2 是可选参数。

  具体来说，就是用一个掩模对每个像素点进行处理，每个像素点在其掩模包括的邻域内按照上面的条件进行判断并处理。因此直方图增强的效果也与掩模的大小有关。

5.直方图分割：

  在直方图中指定一个阈值，小于此阈值的灰度值均置0，大于此阈值的灰度值均置1 。阈值的选取采用如下迭代方法进行：

1. 随机指定一个阈值，计算阈值左右两侧灰度的均值mean1,mean2
2. 求出mean1与mean2的平均值作为新的阈值
3. 重复上述过程直到两次阈值相差小于一个指定精度，得到最终阈值

---

二、具体实现及结果（MATLAB）

第 1 题

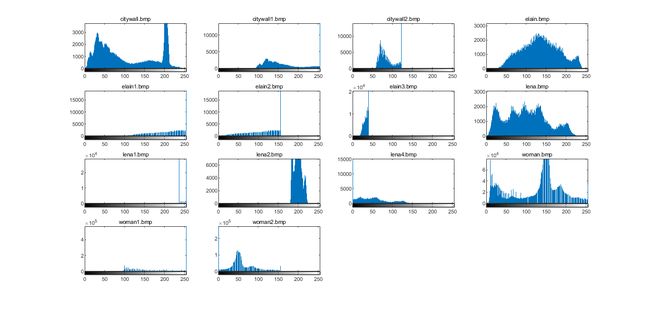
把附件图像的直方图画出

  首先用imread()将图像读入，在这个过程中由于所给图像是采用索引形式存储的，因此需要同时读入图像的索引和调色板，再使用ind2gray()函数将索引图转化为灰度图像，为下面的处理做铺垫。

  直方图可以直接调用内置函数imhist()画出，结果如下所示：

---

第 2 题

把所有图像进行直方图均衡；输出均衡后的图像和源图像进行比对；分析改善内容

  使用histeq()函数实现直方图的均衡，结果如下：

​ 原始图像：

​ 直方图均衡化后图像：

​ 均衡化后的直方图：

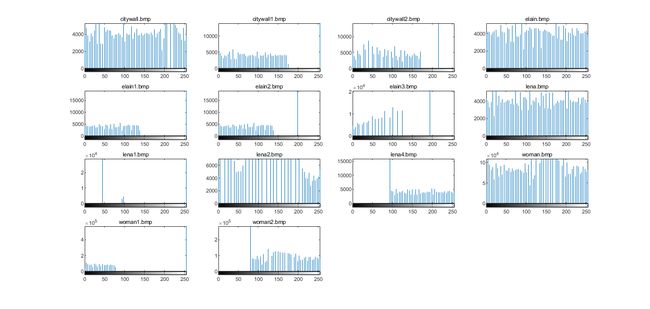
​ 分析： 进行直方图均衡化后，对于对比度小的图像，其对比度显著增强，图像更加清晰可辨识；对于整体色调过亮或过暗的图像，让其色调处在一个适宜的范围，同样更容易被人眼识别。

---

第 3 题

进一步把图像按照对源图像直方图的观察，各自自行指定不同源图像的直方图，进行直方图匹配，进行图像增强

  这里自己构造一个函数histmatch() ，具体内容为：

1. 求输入图像的均衡化直方图T1

2. 求模板图像的均衡化直方图T2

3. 构造转换矩阵T3

4. 得到输出图像

   函数代码如下：(MATLAB)

function img_out=histmatch(img_in,hist)
[M,N]=size(img_in);
hist_img=imhist(img_in);
%求T1：
a=zeros(256,1);
T1=zeros(256,1,'uint8');
a(1)=hist_img(1);
for i=2:256
    a(i)=a(i-1)+hist_img(i);
    T1(i)=uint8(round(a(i)*255/(M*N)));
end
%求T2：
a=zeros(256,1);
T2=zeros(256,1,'uint8');
a(1)=hist(1);
for i=2:256
    a(i)=a(i-1)+hist(i);
    T2(i)=uint8(round(a(i)*255/sum(hist)));
end
%求T3：
T3=zeros(256,1);
a=zeros(256,1);
for i=1:256
    for j=1:256
        a(j)=abs(T1(i)-T2(j));
    end
    [~,p]=min(a);
    T3(i)=uint8(p-1);
end
%outimage:
for i=1:M
    for j=1:N
        img_out(i,j)=T3(uint32(img_in(i,j))+1);
    end
end
img_out=uint8(img_out);
end

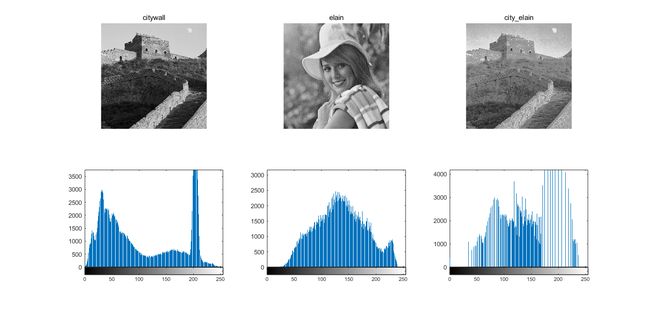
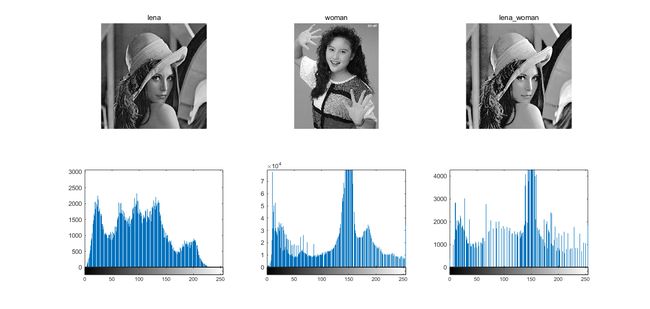
​ 得到结果如下：

1. 将citywall与elain匹配：

2. 将lena和woman进行匹配：

---

第 4 题

对elain和lena图像进行7*7的局部直方图增强

​ 自己构造一个函数LocalHist() ，具体内容为：

1. 参数设置及图像预处理

   • 参数设置包括设置k0,k1,k2,E以及掩模大小masksize，这里选择k0=0.5，k1=0.01，k2=0.5，E=3，masksize=7

   • 图像预处理包括图像扩展及计算全图的灰度均值和方差、标准差

   • 其中图像扩展可以直接调用函数padarray(Img,size,padval,direction) ，其中padval 选择’replicate’将边缘像素点进行复制扩展，direction 选择’both’ 每个方向两边均进行扩展

2. 各像素点掩模覆盖区域参数计算（均值、标准差）

3. 判断条件及处理

   函数代码如下：(MATLAB)

function [Imgout,Imgchange]=LocalHist(Img)
%参数设置及预处理：
k0=0.5;k1=0.01;E=3;k2=0.5;  %设置参数值
masksize = 7;   %邻域大小
Imgex= padarray(Img,[3,3],'replicate','both');%图像扩展
%全图参数计算：
Mg=sum(Img(:))/(size(Img,1)*size(Img,2));%全图均值
sig2g=sum((Img(:)-Mg(:)).^2)/(size(Img,1)*size(Img,2));%全图方差
sigg=sqrt(sig2g);%全图标准差
%各像素点邻域参数计算：
sig2xy=zeros(size(Img));    %用于存储邻域方差
for i=1:size(Img,1)
    for j=1:size(Img,2)
        neibour=Imgex(i:i+6,j:j+6); %邻域截取
        Msxy(i,j)=sum(neibour(:))/masksize^2; %邻域均值
        sig2xy(i,j)=sum((neibour(:)-Msxy(i,j)).^2)/masksize^2;%邻域方差
        sigxy(i,j)=sqrt(sig2xy(i,j));  %邻域标准差
    end
end 
%判断条件：
t1=(Msxy<=k0*Mg);
t2=(sigxy>=k1*sigg)&(sigxy<=k2*sigg);
t=uint8(t1&t2);%需要变化的像素点
t_=uint8((int8(t)-1)*(-1));%无需变化的像素点
Imgchange=Img.*(t*E);   %图像改变部分
Imgnotchange=Img.*t_;   %图像未改变部分
Imgout=Imgchange+Imgnotchange;  %处理后图像
end

​ 得到结果如下：

1. lena增强：

2. elain增强：

---

第 5 题

利用直方图对图像elain和woman进行分割

  自己构造函数Seg()，具体内容为：

1. 设置初始阈值，因为是8位图像，故取T=128

2. 迭代优化，得到最终阈值

3. 按照阈值进行图像分割

函数代码如下：(MATLAB)

function Img_seg=Seg(Img)
hist=imhist(Img);
T=128;T1=0;T0=1;    %设置初始阈值T，设置接受阈值T0，T1用于存储上一次迭代的T
while abs(T-T1)>=T0     %重复以下步骤直到两次阈值相差小于1
    mean1=0;mean2=0;    %mean1,mean2分别为被T分成的两部分的灰度均值
    for i=1:T
        mean1=mean1+hist(i)/sum(hist(1:T))*(i-1);
    end
    for i=T+1:length(hist)
        mean2=mean2+hist(i)/sum(hist(T+1:length(hist)))*(i-1);
    end
    T1=T;
    T=round((mean1+mean2)/2);   %新T值为两侧灰度均值的平均
end
Img_seg=(Img>T);    %灰度大于T的均置为1，其他均置0
end

​ 得到结果如下：

---

参考资料

1. 冈萨雷斯.数字图像处理（第三版）[M].北京:电子工业出版社.2017.1

---

 
 
 

数字图像处理作业链接：
数字图像处理第一次作业——Bmp格式与基本变换
数字图像处理第二次作业——图像仿射变换
数字图像处理第三次作业——基于直方图的图像空域操作
数字图像处理第四次作业——空域滤波与边缘检测
数字图像处理第五次作业——频域滤波器
数字图像处理第六次作业——图像噪声和恢复
数字图像处理第七次作业——图像直线检测