DIDL笔记（pytorch版）（九）

标准化和归一化

标准化处理：(x - x.mean()) / (x.std())处理后的任意一个特征在数据集中所有样本上的均值为0、标准差为1。标准化处理输入数据使各个特征的分布相近：这往往更容易训练出有效的模型。

对深层神经网络来说，即使输入数据已做标准化，训练中模型参数的更新依然很容易造成靠近输出层的输出剧烈变化。在模型训练时，批量归一化利用小批量上的均值和标准差，不断调整神经网络中间输出，从而使整个神经网络在各层的中间输出的数值更稳定。

和丢弃层一样，批量归一化层在训练模式和预测模式下的计算结果也是不一样的。

全连接层批量归一化

位置：仿射变换和激活函数之间。
步骤：

1. 计算输入的均值和方差。注意输入是批量的，即$x^{(1)},...,x^{(m)},x^{(i)}d-dim$
   
2. 计算标准化：
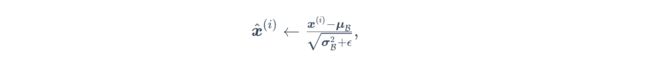
3. 设置拉伸$\gamma$ 初始化1、偏移$\beta$初始化0,分别对应方差和均值，并且与输入相同都是d维向量，$x^{(i)}$分别于他们做按位置乘法和加法运算：
   

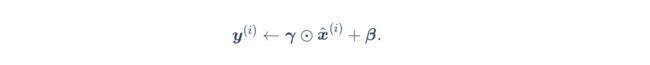
卷积层批量归一化

位置：卷积计算和激活函数之间。
与全连接类似，但是注意卷积是多通道的，所以每个通道都有独立的拉伸和偏移参数。

预测时批量归一化

我们希望模型对于任意输入都有确定的输出。一种常用的方法是通过移动平均估算整个训练数据集的样本均值和方差，并在预测时使用它们得到确定的输出。

def batch_norm(is_training, X, gamma, beta, moving_mean, moving_var, eps, momentum):
    # 判断当前模式是训练模式还是预测模式
    if not is_training:
        # 如果是在预测模式下，直接使用传入的移动平均所得的均值和方差
        X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
    #训练模式
    else:
        assert len(X.shape) in (2, 4)   # 要么二维全连接，要么四维卷积
        if len(X.shape) == 2:
            # 使用全连接层的情况，计算特征维上的均值和方差
            mean = X.mean(dim=0)
            var = ((X - mean) ** 2).mean(dim=0)
        else:
            # 使用二维卷积层的情况，计算通道维上（axis=1）的均值和方差。这里我们需要保持X的形状以便后面可以做广播运算
            # 每个通道都拥有独立的拉伸和偏移参数
            mean = X.mean(dim=0, keepdim=True).mean(dim=2, keepdim=True).mean(dim=3, keepdim=True)
            var = ((X - mean) ** 2).mean(dim=0, keepdim=True).mean(dim=2, keepdim=True).mean(dim=3, keepdim=True)
        # 训练模式下用当前的均值和方差做标准化
        X_hat = (X - mean) / torch.sqrt(var + eps)
        # 更新移动平均的均值和方差
        moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
        moving_var = momentum * moving_var + (1.0 - momentum) * var
    Y = gamma * X_hat + beta  # 拉伸和偏移之后的输出
    return Y, moving_mean, moving_var


class BatchNorm(nn.Module):
    def __init__(self, num_features, num_dims):
        super(BatchNorm, self).__init__()
        # 分辨是全连接还是卷积，num_features为输出个数或者输出通道数
        if num_dims == 2:
            shape = (1, num_features)
        else:
            shape = (1, num_features, 1, 1)
        # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成0和1
        # 卷积的时候每个通道都有自己的gamma和beta
        self.gamma = nn.Parameter(torch.ones(shape))
        self.beta = nn.Parameter(torch.zeros(shape))
        # 不参与求梯度和迭代的变量，全在内存上初始化成0
        self.moving_mean = torch.zeros(shape)
        self.moving_var = torch.zeros(shape)

    def forward(self, X):
        # 如果X不在内存上，将moving_mean和moving_var复制到X所在显存上
        if self.moving_mean.device != X.device:
            self.moving_mean = self.moving_mean.to(X.device)
            self.moving_var = self.moving_var.to(X.device)
        # 保存更新过的moving_mean和moving_var, Module实例的traning属性默认为true, 调用.eval()后设成false
        Y, self.moving_mean, self.moving_var = batch_norm(self.training,
            X, self.gamma, self.beta, self.moving_mean,
            self.moving_var, eps=1e-5, momentum=0.9)
        return Y

net = nn.Sequential(
            nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size
            BatchNorm(6, num_dims=4),
            nn.Sigmoid(),
            nn.MaxPool2d(2, 2), # kernel_size, stride
            nn.Conv2d(6, 16, 5),
            BatchNorm(16, num_dims=4),
            nn.Sigmoid(),
            nn.MaxPool2d(2, 2),
            d2l.FlattenLayer(),
            nn.Linear(16*4*4, 120),
            BatchNorm(120, num_dims=2),
            nn.Sigmoid(),
            nn.Linear(120, 84),
            BatchNorm(84, num_dims=2),
            nn.Sigmoid(),
            nn.Linear(84, 10)
        )

残差网络

背景

随着网络层数的不断提升，模型精度提升，但是到达一定层数时，训练和校验精度反而下降了。

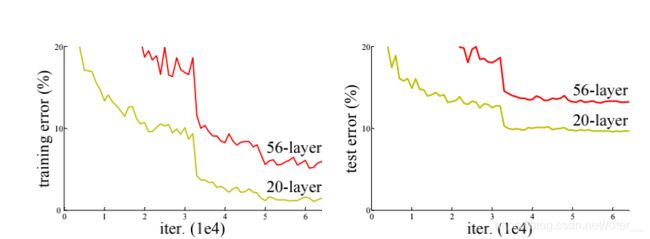
为什么呢？出现了梯度消失，由于反向传播过程中，梯度会逐渐衰减，到最后前面的参数无法进行调整。
如何解决？
也许我们可以把浅层特征传到深层用。从信息论的角度解释，越深feature map特征越少，如果加上前层的不就能保证至少比上一层多了。

残差块

根据上面的思路，作者设置了残差块。残差代表预测值和观测值的差值。误差是衡量观测值和真实值之间的差距。

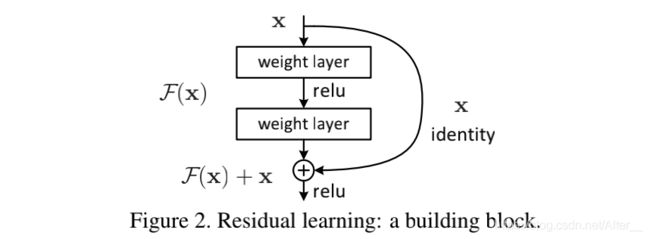
用数学公式证明一下：
直接映射下的残差块表示为：

上面是一层之间的关系。如果我们多写几层，则L与l之间的关系可表示为：

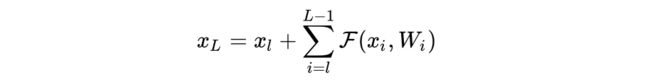
这里我们就可以发现，深层的值可以由任意一个浅层的值加上他们之间的残差部分之和。如果在这个关系上求导：

我们可以发现：残差网络不会出现梯度消失的问题，因为不会永远为0。

参考：https://zhuanlan.zhihu.com/p/42706477

结构以及代码

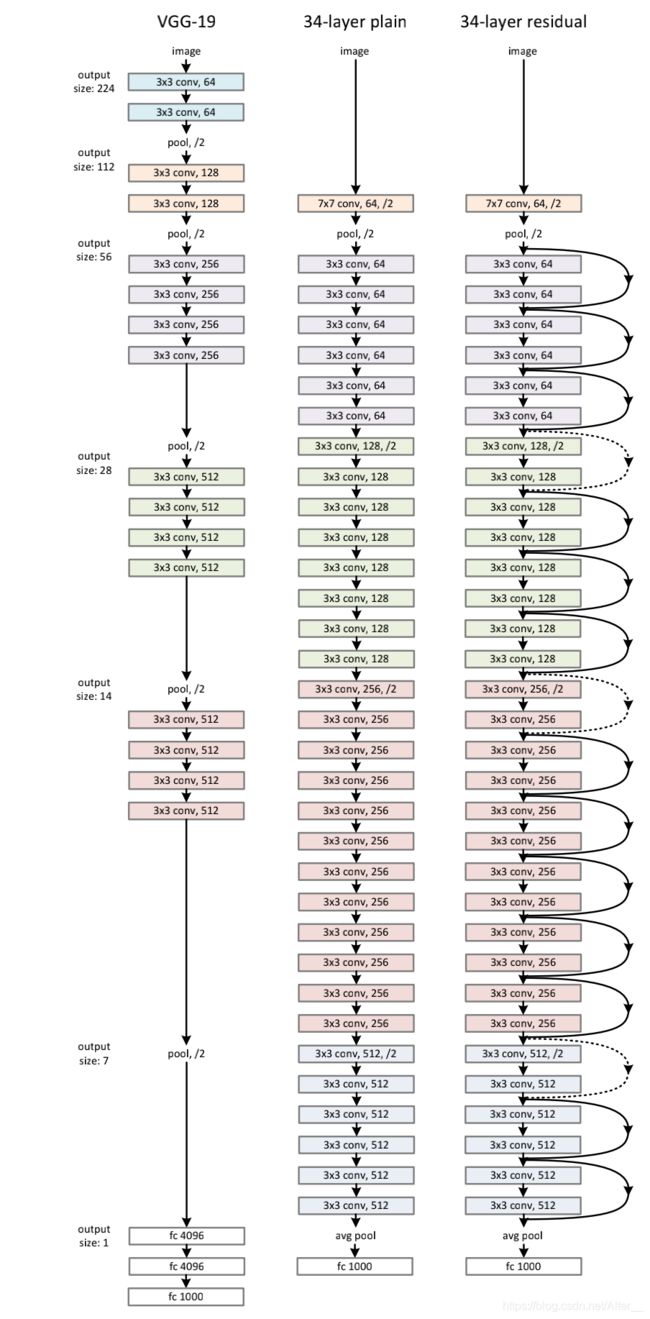
这个时候你就会发现，虚线和实线有什么不同？
如果输入和输出的通道大小相同的时候，我们使用的残差公式就为：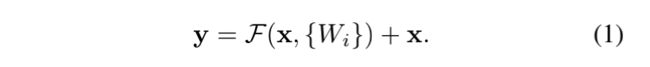
否则：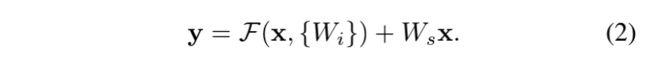
通道不同有两种方法在代码中体现：1. 填充额外的0，使通道变成一样。2. 用1 x 1的卷积匹配出相同的通道数。

class Residual(nn.Module):  # 本类已保存在d2lzh_pytorch包中方便以后使用
    def __init__(self, in_channels, out_channels, use_1x1conv=False, stride=1):
        super(Residual, self).__init__()
        self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1, stride=stride)
        self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1)
        if use_1x1conv:
            self.conv3 = nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=stride)
        else:
            self.conv3 = None
        self.bn1 = nn.BatchNorm2d(out_channels)
        self.bn2 = nn.BatchNorm2d(out_channels)

    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X)))
        Y = self.bn2(self.conv2(Y))
        if self.conv3:
            X = self.conv3(X)
        return F.relu(Y + X)

net = nn.Sequential(
        nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
        nn.BatchNorm2d(64), 
        nn.ReLU(),
        nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

def resnet_block(in_channels, out_channels, num_residuals, first_block=False):
    if first_block:
        assert in_channels == out_channels # 第一个模块的通道数同输入通道数一致
    blk = []
    for i in range(num_residuals):
        if i == 0 and not first_block:
            blk.append(Residual(in_channels, out_channels, use_1x1conv=True, stride=2))
        else:
            blk.append(Residual(out_channels, out_channels))
    return nn.Sequential(*blk)

net.add_module("resnet_block1", resnet_block(64, 64, 2, first_block=True))
net.add_module("resnet_block2", resnet_block(64, 128, 2))
net.add_module("resnet_block3", resnet_block(128, 256, 2))
net.add_module("resnet_block4", resnet_block(256, 512, 2))

net.add_module("global_avg_pool", d2l.GlobalAvgPool2d()) # GlobalAvgPool2d的输出: (Batch, 512, 1, 1)
net.add_module("fc", nn.Sequential(d2l.FlattenLayer(), nn.Linear(512, 10))) 

稠密连接网络

ResNet与DenseNet的区别

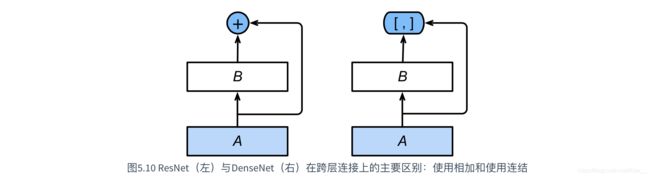
ResNet是在通道上相加，而DenseNet是在通道数上拼接。DenseNet的主要构建模块是稠密块（dense block）和过渡层（transition layer）。而且ResNet是与上一层连接，DenseNet是在每一个稠密块（dense block）中前面层与后面每一层都有连接。

整体连接

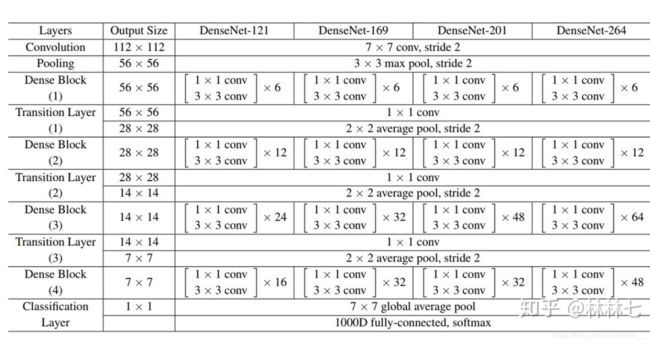
一个稠密块中后面的每一个BottleNeck输出都会与前面的BottleNeck输出有联系。

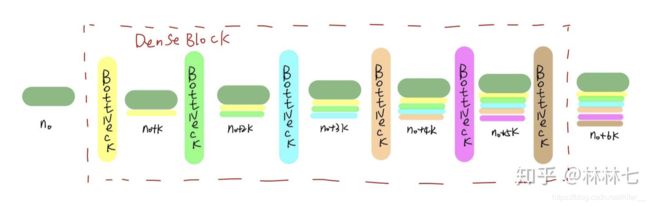
BottleNeck是DenseNet中的“批量归一化、激活和卷积”结构。即一个BottleNeck为[1×1 conv, 3×3 conv]。

由于每个稠密块都会带来通道数的增加，使用过多则会带来过于复杂的模型。过渡层用来控制模型复杂度。它通过1×1卷积层来减小通道数，并使用步幅为2的平均池化层减半高和宽，从而进一步降低模型复杂度。

# 代码和书上略有不同，conv_block加了1*1卷积
import time
import torch
from torch import nn, optim
import torch.nn.functional as F
import d2l as d2l
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')


def conv_block(in_channels, out_channels):
    blk = nn.Sequential(
                        nn.BatchNorm2d(in_channels),
                        nn.ReLU(),
                        nn.Conv2d(in_channels, in_channels, kernel_size=1),

                        nn.BatchNorm2d(in_channels),
                        nn.ReLU(),
                        nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1))
    return blk


# 每一次bottleneck输出通道相同，但是输入通道是累加的
class DenseBlock(nn.Module):
    def __init__(self, num_convs, in_channels, out_channels):
        super(DenseBlock, self).__init__()
        net = []
        for i in range(num_convs):
            in_c = in_channels + i * out_channels
            net.append(conv_block(in_c, out_channels))
        self.net = nn.ModuleList(net)
        self.out_channels = in_channels + num_convs * out_channels # 计算输出通道数

    def forward(self, X):
        for blk in self.net:
            Y = blk(X)
            X = torch.cat((X, Y), dim=1)  # 在通道维上将输入和输出连结
        return X


def transition_block(in_channels, out_channels):
    blk = nn.Sequential(
            nn.BatchNorm2d(in_channels),
            nn.ReLU(),
            nn.Conv2d(in_channels, out_channels, kernel_size=1),
            nn.AvgPool2d(kernel_size=2, stride=2))
    return blk

# 添加网络结构
net = nn.Sequential(
        nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
        nn.BatchNorm2d(64),
        nn.ReLU(),
        nn.MaxPool2d(kernel_size=3, stride=2, padding=1))   # 大小没有变

num_channels, growth_rate = 64, 32          # num_channels为当前的通道数
num_convs_in_dense_blocks = [4, 4, 4, 4]    # 121层还是不要了，太大了

for i, num_convs in enumerate(num_convs_in_dense_blocks):
    DB = DenseBlock(num_convs, num_channels, growth_rate)
    net.add_module("DenseBlosk_%d" % i, DB)
    # 上一个稠密块的输出通道数
    num_channels = DB.out_channels
    # 在稠密块之间加入通道数减半的过渡层
    if i != len(num_convs_in_dense_blocks) - 1:
        net.add_module("transition_block_%d" % i, transition_block(num_channels, num_channels // 2))
        num_channels = num_channels // 2


net.add_module("BN", nn.BatchNorm2d(num_channels))
net.add_module("relu", nn.ReLU())
net.add_module("global_avg_pool", d2l.GlobalAvgPool2d()) # GlobalAvgPool2d的输出: (Batch, num_channels, 1, 1)
net.add_module("fc", nn.Sequential(d2l.FlattenLayer(), nn.Linear(num_channels, 10)))

batch_size = 256
# 如出现“out of memory”的报错信息，可减小batch_size或resize
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)

lr, num_epochs = 0.001, 5
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
d2l.train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs)

参考：
https://blog.csdn.net/zhanghao3389/article/details/85038961
https://zhuanlan.zhihu.com/p/67311529