DIDL笔记（pytorch版）（十一）

前言

已知梯度下降会因为不同维度收敛速度不同导致震荡幅度加大的问题，动量法提出当前梯度方向应充分考虑之前的梯度方向 缓解了梯度震荡幅度大的问题。但是上面两种对于每个维度的梯度值使用同样的学习率，这会导致个别维度收敛速度过慢。

AdaGrad算法，它根据自变量在每个维度的梯度值的大小来调整各个维度上的学习率，从而避免统一的学习率难以适应所有维度的问题。

AdaGrad算法

AdaGrad算法还是有问题的：当学习率在迭代早期降得较快且当前解依然不佳时，AdaGrad算法在迭代后期由于学习率过小，可能较难找到一个有用的解。

这里的学习率eta=0.4，目标函数为$f=x_1^2+2x_2^2$。

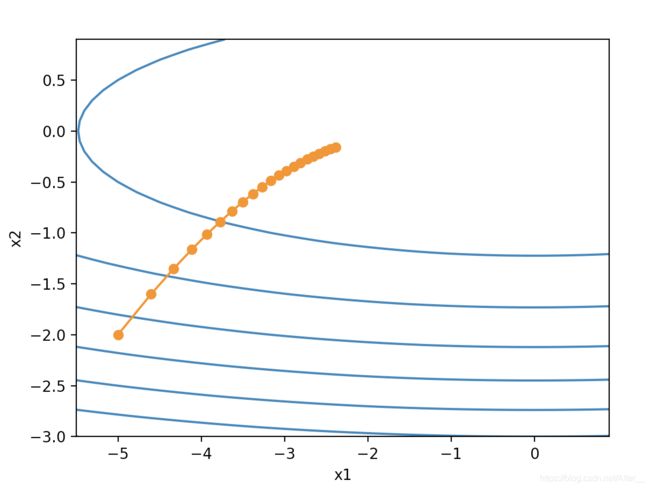
很明显比之前的曲线光滑，在这个背景下，如果eta设置更高，效果会更好。

代码

与之前的动量法相比，初始化和算法计算有变化。

def init_adagrad_states():
    s_w = torch.zeros((features.shape[1], 1), dtype=torch.float32)
    s_b = torch.zeros(1, dtype=torch.float32)
    return (s_w, s_b)


def adagrad(params, states, hyperparams):
    eps = 1e-6
    for p, s in zip(params, states):
        s.data += (p.grad.data**2)
        p.data -= hyperparams['lr'] * p.grad.data / torch.sqrt(s + eps)

RMSProp算法

在上面我们已经暴露出了AdaGrad算法的问题，RMSProp算法对它做了修改。

极其眼熟是不是？我愿把RMSProp算法叫做基于指数加权移动平均的AdaGrad算法。这样一来自变量每个元素的学习率在迭代过程中就不再一直降低（或不变）。

还是同样的目标函数和学习率，RMSProp算法可以更快逼近最优解。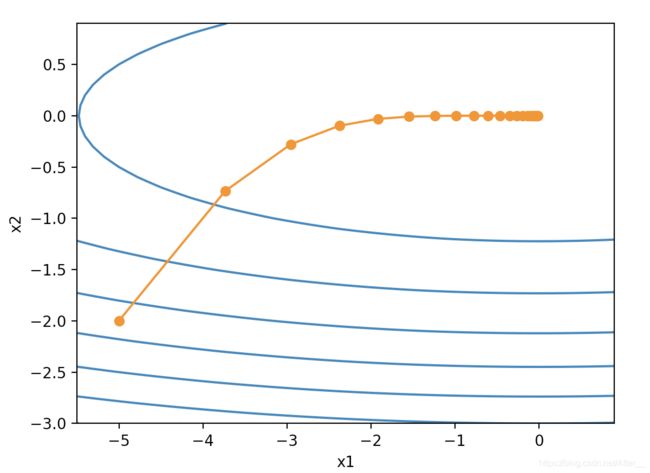

代码

def init_rmsprop_states():
    s_w = torch.zeros((features.shape[1], 1), dtype=torch.float32)
    s_b = torch.zeros(1, dtype=torch.float32)
    return (s_w, s_b)

def rmsprop(params, states, hyperparams):
    gamma, eps = hyperparams['gamma'], 1e-6
    for p, s in zip(params, states):
        s.data = gamma * s.data + (1 - gamma) * (p.grad.data)**2
        p.data -= hyperparams['lr'] * p.grad.data / torch.sqrt(s + eps)

AdaDelta算法

除了RMSProp算法，AdaDelta算法也对AdaGrad算法做出了不同的改进，它没有eta学习率这个超参数了，用另一个代替了。

这个和RMSProp算法一样都有指数加权移动平均。



针对两个不同的超参数，都使用指数加权移动平均。

def init_adadelta_states():
    s_w, s_b = torch.zeros((features.shape[1], 1), dtype=torch.float32), torch.zeros(1, dtype=torch.float32)
    delta_w, delta_b = torch.zeros((features.shape[1], 1), dtype=torch.float32), torch.zeros(1, dtype=torch.float32)
    return ((s_w, delta_w), (s_b, delta_b))

def adadelta(params, states, hyperparams):
    rho, eps = hyperparams['rho'], 1e-5
    for p, (s, delta) in zip(params, states):
        s[:] = rho * s + (1 - rho) * (p.grad.data**2)
        g =  p.grad.data * torch.sqrt((delta + eps) / (s + eps))
        p.data -= g
        delta[:] = rho * delta + (1 - rho) * g * g

Adam算法

Adam算法在RMSProp算法基础上对小批量随机梯度也做了指数加权移动平均。所以Adam算法可以看做是RMSProp算法与动量法的结合。

一样的$s_t$迭代公式。

眼熟的动量法公式之一。

使过去各时间步小批量随机梯度权值之和为1。这也叫作偏差修正。

def init_adam_states():
    v_w, v_b = torch.zeros((features.shape[1], 1), dtype=torch.float32), torch.zeros(1, dtype=torch.float32)
    s_w, s_b = torch.zeros((features.shape[1], 1), dtype=torch.float32), torch.zeros(1, dtype=torch.float32)
    return ((v_w, s_w), (v_b, s_b))

def adam(params, states, hyperparams):
    beta1, beta2, eps = 0.9, 0.999, 1e-6
    for p, (v, s) in zip(params, states):
        v[:] = beta1 * v + (1 - beta1) * p.grad.data
        s[:] = beta2 * s + (1 - beta2) * p.grad.data**2
        v_bias_corr = v / (1 - beta1 ** hyperparams['t'])
        s_bias_corr = s / (1 - beta2 ** hyperparams['t'])
        p.data -= hyperparams['lr'] * v_bias_corr / (torch.sqrt(s_bias_corr) + eps)
    hyperparams['t'] += 1

补充

pytorch中的优化算法调用

torch.optim.SGD(net.paramenters(), lr=0.05)
torch.optim.SGD(net.paramenters(), lr=0.004, momentum=0.9)
torch.optim.Adagrad(net.paramenters(), lr=0.1)
torch.optim.RMSprop(net.paramenters(), lr=0.01, alpha=0.9)
torch.optim.Adadelta(net.paramenters(), rho=0.9)
torch.optim.Adam(net.paramenters(), lr=0.01)