CS231n+assignment2（一）

assignment2目录

CS231n+assignment2（一）

---

---

前言

第二个作业难度还是挺大的，主要实现任意深度的全连接网络。

---

一、环境搭建

作业二需要自己搭建环境，然后导入requirements.txt里面的各种包，这里不再赘述。

二、代码实现

Multi-Layer Fully Connected Network

在本练习中，您将实现一个具有任意数量隐藏层的完全连接的网络。
让我们补全cs231n/classifiers/fc_net.py里面的代码。
在这之前，需要补全cs231n/layers.py里面的前向、反向传播算法以及softmax_loss。在作业一中已经实现，这里不做过多说明。

首先时全连接的前向和反向传播：

def affine_forward(x, w, b):
    """Computes the forward pass for an affine (fully connected) layer.

    The input x has shape (N, d_1, ..., d_k) and contains a minibatch of N
    examples, where each example x[i] has shape (d_1, ..., d_k). We will
    reshape each input into a vector of dimension D = d_1 * ... * d_k, and
    then transform it to an output vector of dimension M.

    Inputs:
    - x: A numpy array containing input data, of shape (N, d_1, ..., d_k)
    - w: A numpy array of weights, of shape (D, M)
    - b: A numpy array of biases, of shape (M,)

    Returns a tuple of:
    - out: output, of shape (N, M)
    - cache: (x, w, b)
    """
    out = None
    x_temp = x.reshape(x.shape[0], -1)
    out = x_temp.dot(w) + b
    cache = (x, w, b)
    return out, cache

def affine_backward(dout, cache):
    """Computes the backward pass for an affine (fully connected) layer.

    Inputs:
    - dout: Upstream derivative, of shape (N, M)
    - cache: Tuple of:
      - x: Input data, of shape (N, d_1, ... d_k)
      - w: Weights, of shape (D, M)
      - b: Biases, of shape (M,)

    Returns a tuple of:
    - dx: Gradient with respect to x, of shape (N, d1, ..., d_k)
    - dw: Gradient with respect to w, of shape (D, M)
    - db: Gradient with respect to b, of shape (M,)
    """
    x, w, b = cache
    dx, dw, db = None, None, None
    x_temp = np.reshape(x, (x.shape[0], -1))
    db = np.sum(dout, axis=0, keepdims=True)
    dw = np.dot(x_temp.T, dout)
    dx = np.dot(dout, w.T)
    dx = np.reshape(dx, x.shape)
    return dx, dw, db

激活函数:

def relu_forward(x):
    """Computes the forward pass for a layer of rectified linear units (ReLUs).

    Input:
    - x: Inputs, of any shape

    Returns a tuple of:
    - out: Output, of the same shape as x
    - cache: x
    """
    out = None
    out = np.maximum(0, x)
    cache = x
    return out, cache


def relu_backward(dout, cache):
    """Computes the backward pass for a layer of rectified linear units (ReLUs).

    Input:
    - dout: Upstream derivatives, of any shape
    - cache: Input x, of same shape as dout

    Returns:
    - dx: Gradient with respect to x
    """
    dx, x = None, cache
    dx = dout
    dx[x <= 0] = 0
    return dx

softmax_loss:

def softmax_loss(x, y):
    """Computes the loss and gradient for softmax classification.

    Inputs:
    - x: Input data, of shape (N, C) where x[i, j] is the score for the jth
      class for the ith input.
    - y: Vector of labels, of shape (N,) where y[i] is the label for x[i] and
      0 <= y[i] < C

    Returns a tuple of:
    - loss: Scalar giving the loss
    - dx: Gradient of the loss with respect to x
    """
    loss, dx = None, None
    num = len(x)
    x_scores = x[range(num), y]
    loss = np.sum(- np.log(np.exp(x_scores) / np.sum(np.exp(x), axis=1))) / num
    dx = np.zeros_like(x)
    dx = np.exp(x) / np.sum(np.exp(x), axis=1, keepdims=True)
    dx[range(num), y] -= 1
    dx /= num
    return loss, dx

实现上述代码后，加载数据。

Initial Loss and Gradient Check

接着我们需要完成模型的初始化，打开fc_net.py文件。
首先需要实现模型参数的初始化
将w初始化为标准高斯分布的随机数，将b初始化为0。同时如果需要归一化则将scale初始化为1，shift初始化为0。

layers_dims = [input_dim] + hidden_dims + [num_classes]
for i in range(self.num_layers):
	self.params[f'W{i+1}'] = np.random.randn(layers_dims[i], layers_dims[i+1]) * weight_scale
    self.params[f'b{i+1}'] = np.zeros(shape=(1, layers_dims[i+1]))
    if normalization == 'batchnorm' and i < len(hidden_dims):
    	self.params[f'gamma{i}'] = np.ones((1, layers_dims[i + 1]))
        self.params[f'beta{i}'] = np.zeros((1, layers_dims[i + 1]))

接着将loss的代码补全：
这里需要注意的是，在计算输出时，不需要激活。normlization代码可暂时忽略。

h, cache1, cache2, cache3, cache4, bn, out = {}, {}, {}, {}, {}, {}, {}
out[0] = X
for i in range(self.num_layers - 1):
    w, b = self.params[f'W{i+1}'], self.params[f'b{i+1}']
    if self.normalization != None:
        gamma, beta = self.params[f'gamma{i + 1}'], self.params[f'beta{i + 1}']
        h[i], cache1[i] = affine_forward(out[i], w, b)
        if self.normalization == 'batchnorm':
            bn[i], cache2[i] = batchnorm_forward(h[i], gamma, beta, self.bn_params)
        else:
            bn[i], cache2[i] = layernorm_forward(h[i], gamma, beta, self.bn_params)
        out[i+1], cache3[i] = relu_forward(bn[i])
        if self.use_dropout:
            out[i+1], cache4[i] = dropout_forward(out[i+1], self.dropout_param)
    else:
        out[i+1], cache3[i] = affine_relu_forward(out[i], w, b)
        if self.use_dropout:
            out[i+1], cache4[i] = dropout_forward(out[i+1], self.dropout_param)
 W, b = self.params[f'W{self.num_layers}'], self.params[f'b{self.num_layers}']
 scores, cache = affine_forward(out[self.num_layers - 1], W, b)

完成以上代码，就可以运行剩下的作业。

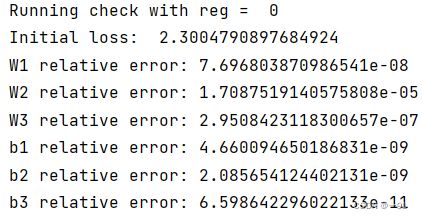
np.random.seed(231)
N, D, H1, H2, C = 2, 15, 20, 30, 10
X = np.random.randn(N, D)
y = np.random.randint(C, size=(N,))

for reg in [0, 3.14]:
    print("Running check with reg = ", reg)
    model = FullyConnectedNet(
        [H1, H2],
        input_dim=D,
        num_classes=C,
        reg=reg,
        weight_scale=5e-2,
        dtype=np.float64
    )

    loss, grads = model.loss(X, y)
    print("Initial loss: ", loss)

    # Most of the errors should be on the order of e-7 or smaller.   
    # NOTE: It is fine however to see an error for W2 on the order of e-5
    # for the check when reg = 0.0
    for name in sorted(grads):
        f = lambda _: model.loss(X, y)[0]
        grad_num = eval_numerical_gradient(f, model.params[name], verbose=False, h=1e-5)
        print(f"{name} relative error: {rel_error(grad_num, grads[name])}")

若上面的代码没有问题，这里代码的结果除w2在e-5，大部分应该都是e-7或者更小。

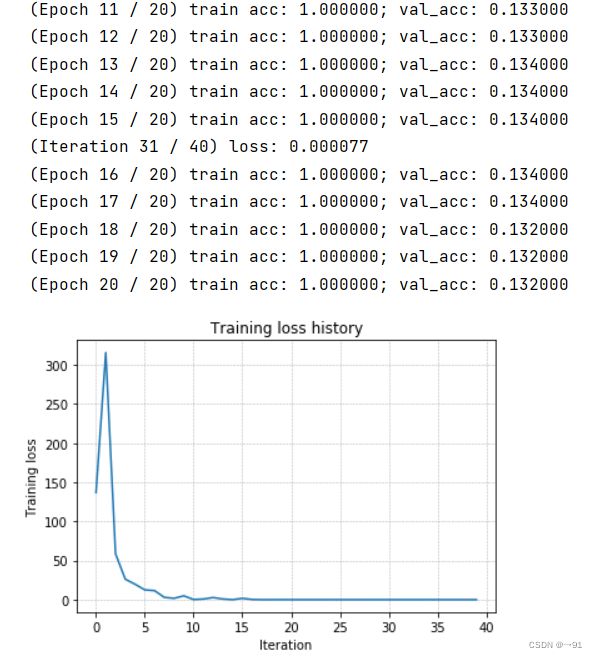
# TODO: Use a three-layer Net to overfit 50 training examples by 
# tweaking just the learning rate and initialization scale.

num_train = 50
small_data = {
  "X_train": data["X_train"][:num_train],
  "y_train": data["y_train"][:num_train],
  "X_val": data["X_val"],
  "y_val": data["y_val"],
}

weight_scale = 1e-2   # Experiment with this!
learning_rate = 1e-2  # Experiment with this!
model = FullyConnectedNet(
    [100, 100],
    weight_scale=weight_scale,
    dtype=np.float64
)
solver = Solver(
    model,
    small_data,
    print_every=10,
    num_epochs=20,
    batch_size=25,
    update_rule="sgd",
    optim_config={"learning_rate": learning_rate},
)
solver.train()

plt.plot(solver.loss_history)
plt.title("Training loss history")
plt.xlabel("Iteration")
plt.ylabel("Training loss")
plt.grid(linestyle='--', linewidth=0.5)
plt.show()

这里需要修改learning_rate和weight_scale让training accuracy达到100%，我这里修改：
weight_scale = 1e-2
learning_rate = 1e-2

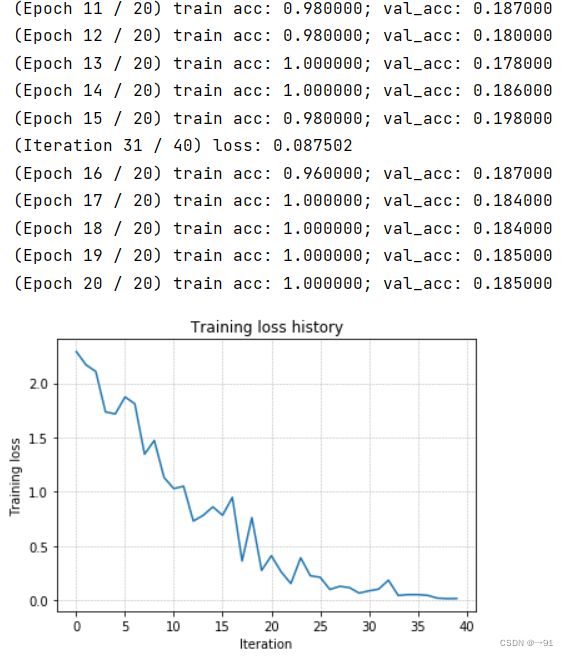
# TODO: Use a five-layer Net to overfit 50 training examples by 
# tweaking just the learning rate and initialization scale.

num_train = 50
small_data = {
  'X_train': data['X_train'][:num_train],
  'y_train': data['y_train'][:num_train],
  'X_val': data['X_val'],
  'y_val': data['y_val'],
}

learning_rate = 1e-3  # Experiment with this!
weight_scale = 1e-1   # Experiment with this!
model = FullyConnectedNet(
    [100, 100, 100, 100],
    weight_scale=weight_scale,
    dtype=np.float64
)
solver = Solver(
    model,
    small_data,
    print_every=10,
    num_epochs=20,
    batch_size=25,
    update_rule='sgd',
    optim_config={'learning_rate': learning_rate},
)
solver.train()

plt.plot(solver.loss_history)
plt.title('Training loss history')
plt.xlabel('Iteration')
plt.ylabel('Training loss')
plt.grid(linestyle='--', linewidth=0.5)
plt.show()

这里和上面一样，只是网络层数变为5层。

Question1

Did you notice anything about the comparative difficulty of training the three-layer network vs. training the five-layer network? In particular, based on your experience, which network seemed more sensitive to the initialization scale? Why do you think that is the case?
答案显而易见，五层网络有更多的参数，肯定更难训练，根据图像五层网络的初始误差较大，且训练较难，即对初始化规模更敏感。

SGD+Momentum

这里我们需要完成cs231n/optim.py各个优化器模块。
又被称为动量法，我个人简单的理解是，在更新梯度的时候，我们要注意保留之前的梯度的信息，可以很好的处理导数为0的情况。

def sgd_momentum(w, dw, config=None):
    """
    Performs stochastic gradient descent with momentum.

    config format:
    - learning_rate: Scalar learning rate.
    - momentum: Scalar between 0 and 1 giving the momentum value.
      Setting momentum = 0 reduces to sgd.
    - velocity: A numpy array of the same shape as w and dw used to store a
      moving average of the gradients.
    """
    if config is None:
        config = {}
    config.setdefault("learning_rate", 1e-2)
    config.setdefault("momentum", 0.9)
    v = config.get("velocity", np.zeros_like(w))
    next_w = None
    v = config['momentum'] * v - config['learning_rate'] * dw
    next_w = w + v
    config["velocity"] = v
    return next_w, config

然后运行下面的代码，若error在e-9量级则代码没有问题。

from cs231n.optim import sgd_momentum

N, D = 4, 5
w = np.linspace(-0.4, 0.6, num=N*D).reshape(N, D)
dw = np.linspace(-0.6, 0.4, num=N*D).reshape(N, D)
v = np.linspace(0.6, 0.9, num=N*D).reshape(N, D)

config = {"learning_rate": 1e-3, "velocity": v}
next_w, _ = sgd_momentum(w, dw, config=config)

expected_next_w = np.asarray([
  [ 0.1406,      0.20738947,  0.27417895,  0.34096842,  0.40775789],
  [ 0.47454737,  0.54133684,  0.60812632,  0.67491579,  0.74170526],
  [ 0.80849474,  0.87528421,  0.94207368,  1.00886316,  1.07565263],
  [ 1.14244211,  1.20923158,  1.27602105,  1.34281053,  1.4096    ]])
expected_velocity = np.asarray([
  [ 0.5406,      0.55475789,  0.56891579, 0.58307368,  0.59723158],
  [ 0.61138947,  0.62554737,  0.63970526,  0.65386316,  0.66802105],
  [ 0.68217895,  0.69633684,  0.71049474,  0.72465263,  0.73881053],
  [ 0.75296842,  0.76712632,  0.78128421,  0.79544211,  0.8096    ]])

# Should see relative errors around e-8 or less
print("next_w error: ", rel_error(next_w, expected_next_w))
print("velocity error: ", rel_error(expected_velocity, config["velocity"]))

继续运行下面的代码，会发现动量方法的收敛速度是要优于SGD的。

num_train = 4000
small_data = {
  'X_train': data['X_train'][:num_train],
  'y_train': data['y_train'][:num_train],
  'X_val': data['X_val'],
  'y_val': data['y_val'],
}

solvers = {}

for update_rule in ['sgd', 'sgd_momentum']:
    print('Running with ', update_rule)
    model = FullyConnectedNet(
        [100, 100, 100, 100, 100],
        weight_scale=5e-2
    )

    solver = Solver(
        model,
        small_data,
        num_epochs=5,
        batch_size=100,
        update_rule=update_rule,
        optim_config={'learning_rate': 5e-3},
        verbose=True,
    )
    solvers[update_rule] = solver
    solver.train()

fig, axes = plt.subplots(3, 1, figsize=(15, 15))

axes[0].set_title('Training loss')
axes[0].set_xlabel('Iteration')
axes[1].set_title('Training accuracy')
axes[1].set_xlabel('Epoch')
axes[2].set_title('Validation accuracy')
axes[2].set_xlabel('Epoch')

for update_rule, solver in solvers.items():
    axes[0].plot(solver.loss_history, label=f"loss_{update_rule}")
    axes[1].plot(solver.train_acc_history, label=f"train_acc_{update_rule}")
    axes[2].plot(solver.val_acc_history, label=f"val_acc_{update_rule}")
    
for ax in axes:
    ax.legend(loc="best", ncol=4)
    ax.grid(linestyle='--', linewidth=0.5)

plt.show()

RMSProp and Adam

对于rmsprop，个人理解就是通过调整不同维的学习率，让梯度大的维度学习率小，梯度小的学习率大，同时改进了学习率越来越小的问题。

def rmsprop(w, dw, config=None):
    """
    Uses the RMSProp update rule, which uses a moving average of squared
    gradient values to set adaptive per-parameter learning rates.

    config format:
    - learning_rate: Scalar learning rate.
    - decay_rate: Scalar between 0 and 1 giving the decay rate for the squared
      gradient cache.
    - epsilon: Small scalar used for smoothing to avoid dividing by zero.
    - cache: Moving average of second moments of gradients.
    """
    if config is None:
        config = {}
    config.setdefault("learning_rate", 1e-2)
    config.setdefault("decay_rate", 0.99)
    config.setdefault("epsilon", 1e-8)
    config.setdefault("cache", np.zeros_like(w))
    next_w = None
    cache = config['cache']
    decay_rate = config['decay_rate']
    epsilon = config['epsilon']
    learning_rate = config['learning_rate']
    cache = decay_rate * cache + (1 - decay_rate) * (dw ** 2)
    w -= learning_rate * dw / (np.sqrt(cache) + epsilon)
    config['cache'] = cache
    next_w = w
    return next_w, config

adam融合了上述两种方法的优点，是优先考虑的优化器。需要注意的是，我们需要实现的是完整的Adam更新规则（带有偏差校正机制），而不是课程中提到的第一个简化版本。

def adam(w, dw, config=None):
    """
    Uses the Adam update rule, which incorporates moving averages of both the
    gradient and its square and a bias correction term.

    config format:
    - learning_rate: Scalar learning rate.
    - beta1: Decay rate for moving average of first moment of gradient.
    - beta2: Decay rate for moving average of second moment of gradient.
    - epsilon: Small scalar used for smoothing to avoid dividing by zero.
    - m: Moving average of gradient.
    - v: Moving average of squared gradient.
    - t: Iteration number.
    """
    if config is None:
        config = {}
    config.setdefault("learning_rate", 1e-3)
    config.setdefault("beta1", 0.9)
    config.setdefault("beta2", 0.999)
    config.setdefault("epsilon", 1e-8)
    config.setdefault("m", np.zeros_like(w))
    config.setdefault("v", np.zeros_like(w))
    config.setdefault("t", 0)
    next_w = None
    learning_rate = config['learning_rate']
    beta1 = config['beta1']
    beta2 = config['beta2']
    m = config['m']
    v = config['v']
    epsilon = config['epsilon']
    t = config['t']
    t += 1
    m = beta1 * m + (1 - beta1) * dw
    v = beta2 * v + (1 - beta2) * (dw**2)
    m_bias = m / (1 - beta1**t)
    v_bias = v / (1 - beta2**t)
    w -= learning_rate * m_bias / (np.sqrt(v_bias) + epsilon)
    config['m'] = m
    config['v'] = v
    config['t'] = t
    return next_w, config

运行下面的代码：

# Test RMSProp implementation
from cs231n.optim import rmsprop

N, D = 4, 5
w = np.linspace(-0.4, 0.6, num=N*D).reshape(N, D)
dw = np.linspace(-0.6, 0.4, num=N*D).reshape(N, D)
cache = np.linspace(0.6, 0.9, num=N*D).reshape(N, D)

config = {'learning_rate': 1e-2, 'cache': cache}
next_w, _ = rmsprop(w, dw, config=config)

expected_next_w = np.asarray([
  [-0.39223849, -0.34037513, -0.28849239, -0.23659121, -0.18467247],
  [-0.132737,   -0.08078555, -0.02881884,  0.02316247,  0.07515774],
  [ 0.12716641,  0.17918792,  0.23122175,  0.28326742,  0.33532447],
  [ 0.38739248,  0.43947102,  0.49155973,  0.54365823,  0.59576619]])
expected_cache = np.asarray([
  [ 0.5976,      0.6126277,   0.6277108,   0.64284931,  0.65804321],
  [ 0.67329252,  0.68859723,  0.70395734,  0.71937285,  0.73484377],
  [ 0.75037008,  0.7659518,   0.78158892,  0.79728144,  0.81302936],
  [ 0.82883269,  0.84469141,  0.86060554,  0.87657507,  0.8926    ]])

# You should see relative errors around e-7 or less
print('next_w error: ', rel_error(expected_next_w, next_w))
print('cache error: ', rel_error(expected_cache, config['cache']))

# Test Adam implementation
from cs231n.optim import adam

N, D = 4, 5
w = np.linspace(-0.4, 0.6, num=N*D).reshape(N, D)
dw = np.linspace(-0.6, 0.4, num=N*D).reshape(N, D)
m = np.linspace(0.6, 0.9, num=N*D).reshape(N, D)
v = np.linspace(0.7, 0.5, num=N*D).reshape(N, D)

config = {'learning_rate': 1e-2, 'm': m, 'v': v, 't': 5}
next_w, _ = adam(w, dw, config=config)

expected_next_w = np.asarray([
  [-0.40094747, -0.34836187, -0.29577703, -0.24319299, -0.19060977],
  [-0.1380274,  -0.08544591, -0.03286534,  0.01971428,  0.0722929],
  [ 0.1248705,   0.17744702,  0.23002243,  0.28259667,  0.33516969],
  [ 0.38774145,  0.44031188,  0.49288093,  0.54544852,  0.59801459]])
expected_v = np.asarray([
  [ 0.69966,     0.68908382,  0.67851319,  0.66794809,  0.65738853,],
  [ 0.64683452,  0.63628604,  0.6257431,   0.61520571,  0.60467385,],
  [ 0.59414753,  0.58362676,  0.57311152,  0.56260183,  0.55209767,],
  [ 0.54159906,  0.53110598,  0.52061845,  0.51013645,  0.49966,   ]])
expected_m = np.asarray([
  [ 0.48,        0.49947368,  0.51894737,  0.53842105,  0.55789474],
  [ 0.57736842,  0.59684211,  0.61631579,  0.63578947,  0.65526316],
  [ 0.67473684,  0.69421053,  0.71368421,  0.73315789,  0.75263158],
  [ 0.77210526,  0.79157895,  0.81105263,  0.83052632,  0.85      ]])

# You should see relative errors around e-7 or less
print('next_w error: ', rel_error(expected_next_w, next_w))
print('v error: ', rel_error(expected_v, config['v']))
print('m error: ', rel_error(expected_m, config['m']))

对比上述所有的优化器。

learning_rates = {'rmsprop': 1e-4, 'adam': 1e-3}
for update_rule in ['adam', 'rmsprop']:
    print('Running with ', update_rule)
    model = FullyConnectedNet(
        [100, 100, 100, 100, 100],
        weight_scale=5e-2
    )
    solver = Solver(
        model,
        small_data,
        num_epochs=5,
        batch_size=100,
        update_rule=update_rule,
        optim_config={'learning_rate': learning_rates[update_rule]},
        verbose=True
    )
    solvers[update_rule] = solver
    solver.train()
    print()
    
fig, axes = plt.subplots(3, 1, figsize=(15, 15))

axes[0].set_title('Training loss')
axes[0].set_xlabel('Iteration')
axes[1].set_title('Training accuracy')
axes[1].set_xlabel('Epoch')
axes[2].set_title('Validation accuracy')
axes[2].set_xlabel('Epoch')

for update_rule, solver in solvers.items():
    axes[0].plot(solver.loss_history, label=f"{update_rule}")
    axes[1].plot(solver.train_acc_history, label=f"{update_rule}")
    axes[2].plot(solver.val_acc_history, label=f"{update_rule}")
    
for ax in axes:
    ax.legend(loc='best', ncol=4)
    ax.grid(linestyle='--', linewidth=0.5)

plt.show()

对比发现，Adam的效果是非常好的。

Question 2:

AdaGrad, like Adam, is a per-parameter optimization method that uses the following update rule:

cache += dw**2
w += - learning_rate * dw / (np.sqrt(cache) + eps)

John notices that when he was training a network with AdaGrad that the updates became very small, and that his network was learning slowly. Using your knowledge of the AdaGrad update rule, why do you think the updates would become very small? Would Adam have the same issue?
答案是显而易见的，因为cache 一直在不停的增大，学习率肯定会越变越小，所以要采取一定措施来避免这个问题。

Train a Good Model!

这里需要自己构建一个优秀的网络，就不再赘述可以参考我另外的文章cifar-10。