无人机辅助移动边缘计算的计算卸载优化:一种深度确定性策略梯度方法（3）——基础知识

无人机辅助移动边缘计算的计算卸载优化:一种深度确定性策略梯度方法（3）——基础知识

参考文献：

[1] Wang Y , Fang W , Ding Y , et al. Computation offloading optimization for UAV-assisted mobile edge computing: a deep deterministic policy gradient approach[J]. Wireless Networks, 2021:1-16.doi：https://doi.org/10.1007/s11276-021-02632-z

3 基于DDPG的计算卸载优化

在本节中，我们首先介绍MDP、Q-Learning、DQN和DDPG这些重要的新兴RL技术的基本知识。然后，讨论了如何利用DDPG来训练无人机辅助MEC系统的高效计算卸载策略。详细地定义了状态空间、动作空间和奖励函数，描述了数据预处理的状态归一化，并举例说明了训练算法和测试算法的过程。

3.1 RL介绍

3.1.1 MDP

MDP是描述离散时间随机控制过程的数学框架，在该过程中，结果是部分随机的，并且处于主体或决策者的控制下。它正式地描述了一个环境，它是完全可观察到的强化学习。通常，MDP可以定义为一个元组 $(\mathcal{S},\mathcal{A},p(.,.),r)$ ，S 是状态空间， A 是动作空间，$p(s_{i+1}|s_i,a_i)$ 是执行动作 $a_i\in \mathcal{A}$ 从当前状态 $s_i\in \mathcal{S}$ 到下一状态 $s_{i+1}\in \mathcal{S}$ 的转移概率，同时 $r: \mathcal S \times \mathcal{A} \rightarrow \mathcal R $是即时/即时奖励功能。我们表示 $\pi : \mathcal S \rightarrow \mathcal P(\mathcal A) $ 作为一个“策略”，它是从一个状态映射到一个动作。MDP的目标是找到一个最优的政策，可以最大化预期的累积回报:
$$R_i=\sum _{l=i}^{\infty }{\gamma }^{l-i}{r}_l$$
其中, $\gamma \in [0,1]$ 是折扣因子， $r_l=r(s_l,a_l)$ 是第 $l$ 个时间段的即时奖励。在策略 $\pi$ 下，状态 $s_i$ 的预期折现收益定义为状态值函数，即
$$V_{\pi }\left(s_i\right)={\mathbb{E}}_{\pi }\left[R_i\mid s_i\right]$$
同样，在策略 $\pi$ 下，$s_i$ 状态下采取行动 $a_i$后的预期折现收益定义为一个行动值函数，即:
$$Q_{\pi }\left(s_i\right)={\mathbb{E}}_{\pi }\left[R_i\mid s_i,a_i\right]$$
根据Bellman方程，状态值函数和动作值函数的递归关系分别表示为:
$$\begin{array}{l}{V}_{\pi }\left(s_i\right)={\mathbb{E}}_{\pi }\left[r\left(s_i,a_i\right)+\gamma V_{\pi }\left(s_{i+1}\right)\right]\\ Q_{\pi }\left(s_i,a_i\right)={\mathbb{E}}_{\pi }\left[r\left(s_i,a_i\right)+\gamma Q_{\pi }\left(s_{i+1},a_{i+1}\right)\right]\end{array}$$
既然我们的目标是找到最优的政策 $\pi \ast$ 时，可通过最优值函数求出各状态下的最优动作。最优状态值函数可以表示为:
$$V_{\ast }\left(s_i\right)=\underset{a_i\in \mathcal{A}}{\max }{\mathbb{E}}_{\pi }\left[r\left(s_i,a_i\right)+\gamma V_{\pi }\left(s_{i+1}\right)\right].$$
最优行为值函数也遵循最优策略 $\pi \ast$ ，我们可以写出 用 $Q_{\ast }$ 使用 $V_{\ast }$ 表示如下:
$$Q_{\ast }\left(s_i,a_i\right)={\mathbb{E}}_{\pi }\left[r\left(s_i,a_i\right)+\gamma V_{\ast }\left(s_{i+1}\right)\right]$$

3.1.2 Q-learning

RL是机器学习的一个重要分支，agent通过与控制环境交互，使其达到最优状态，从而获得最大的收益。虽然RL常用于解决 MDPs 的优化问题，但潜在传播概率 $p(s_{i+1}|s_i,a_i)$ 是未知的，甚至是不稳定的。在RL中，agent试图通过与控制环境的交互，并通过之前的经验调整自己的行为来获得最大的回报。Q-learning 是 RL 中一种流行而有效的方法，它是一种 off-policy 时差(TD)控制算法。状态-行为函数即最优Q函数的Bellman最优方程可以表示为:
$$Q_{\ast }\left(s_i,a_i\right)={\mathbb{E}}_{\pi }\left[r\left(s_i,a_i\right)+\gamma \underset{a_{i+1}}{\max }{Q}_{\ast }\left(s_{i+1},a_{i+1}\right)\right]$$
通过迭代过程可以找到Q函数的最优值。agent从经验元组 $(s_i,a_i,r_i,s_{i+1})$ 学习,Q函数可在第 i 步时间更新如下:
$$Q(s_i,a_i)\leftarrow Q(s_i,a_i)+\alpha [r(s_i,a_i)+\gamma \underset{a_{i+1}}{\max }Q(s_{i+1},a_{i+1})-Q(s_i,a_i)]$$
其中， $\alpha$ 为学习率， $r(s_i,a_i)+\gamma {\max }_{a_{i+1}}Q(s_{i+1},a_{i+1})$ 为预测的Q值， $Q(s_i,a_i)$ 是当前Q值。预测Q值和当前Q值之间的差就是TD误差。当选择合适的学习速率时，Q学习算法收敛。

3.1.3 DQN

Q-learning算法通过维护一个查询表更新状态动作空间中各项的Q值，适用于状态动作空间较小的情况。**考虑到实际系统模型的复杂性，这些空间通常是非常大的。原因是大量状态很少被访问，对应的Q值很少更新，导致Q函数的收敛时间较长。**DQN通过将深度神经网络(DNNs)与q学习相结合，解决了Q-learning算法的不足。DQN的核心思想是利用 $\theta$ 参数化的DNN来求得近似的Q值 $Q(s,a)$ 代替 Q 表，即 $Q(s,a\mid \theta )\approx Q_{\ast }(s,a)$ 。

但是使用 DNN 的 RL 算法的稳定性不能得到保证。为了解决这个问题，采用了两种机制。第一个是体验重放（experience replay）。在每个时间步 i 中，agent的交互经验元组 $\left(s_i,a_i,r_i,s_{i+1}\right)$ 存储在经验重放缓冲区，即经验池 $B_m$。然后，从经验池中随机选取少量样本，即小批量，对深度神经网络的参数进行训练，而不是直接使用连续样本进行训练。第二种稳定方法是使用一个目标网络，它最初包含了设定策略的网络的权值，但在固定的时间步长内保持冻结状态。目标Q网络更新缓慢，但主Q网络更新频繁。这样大大降低了目标与估计Q值之间的相关性，使得算法更加稳定。

在每次迭代中，通过最小化损失函数 $L(\theta )$，将深度 Q 函数训练到目标值。损失函数可以写成:
$$L(\theta )=\mathbb{E}\left[(y-Q(s,a\mid \theta ){)}^2\right]$$
其中目标值 y 表示为 $y=r+\gamma {\max }_{a^{\prime }}Q\left(s^{\prime },a^{\prime }\mid {\theta }_i^{-}\right)$ 。在 Q-learning 中，权值 ${\theta }_i^{-}={\theta }_{i-1}$ ，而在深度 q 学习 ${\theta }_i^{-}={\theta }_{1-X}$ ，即目标网络权值每 X 个时间步更新一次。

3.1.4 DDPG

DQN算法虽然可以解决高维状态空间的问题，但仍然不能处理连续的动作空间。DDPG算法是一种基于DNN的无模型的 off-policy actor - critic算法，可以学习连续动作空间中的策略。该算法由策略函数和 q 值函数组成。策略函数扮演一个参与者来生成动作。q 值函数作为一个批评家，评价行为人的表现，并指导行为人的后续行动。

如图1所示，DDPG使用两个不同的 DNNs 来逼近actor网络 $\mu \left(s\mid {\theta }^{\mu }\right)$ (即policy function)和critic 网络 $Q\left(s,a\mid {\theta }^Q\right)$ (即Q-value funtion)。另外，行动者网络和批评网络都包含一个与它们结构相同的目标网络:使用参数 ${\theta }^{{\mu }^{\prime }}$ 的行动者目标网络 ${\mu }^{\prime }$ ，使用参数 ${\theta }^{Q^{\prime }}$ 的批评目标网络 $Q^{\prime }$。与 DQN 相似，批评家网络 $Q\left(s,a\mid {\theta }^Q\right)$ 可以更新如下:
$$L\left({\theta }^Q\right)={\mathbb{E}}_{{\mu }^{\prime }}\left[{\left(y_i-Q\left(s_i,a_i\mid {\theta }^Q\right)\right)}^2\right]$$
其中，
$$y_i=r_i+\gamma Q\left(s_{i+1},\mu \left(s_{i+1}\right)\mid {\theta }^Q\right)$$
正如Silver等人所证明的，策略梯度可以用链式法则更新，
$$\begin{array}{r}{\nabla }_{{\theta }^{\mu }}J\approx {\mathbb{E}}_{{\mu }^{\prime }}\left[{{\nabla }_{{\theta }^{\mu }}Q\left(s,a\mid {\theta }^Q\right)|}_{s=s_i,a=\mu \left(s_i\mid {\theta }^{\mu }\right)}\right]\\ ={\mathbb{E}}_{{\mu }^{\prime }}\left[{{{\nabla }_{a}Q\left(s,a\mid {\theta }^Q\right)|}_{s=s_i,a=\mu \left(s_i\mid {\theta }^{\mu }\right)}{\nabla }_{{\theta }^{\mu }}\mu \left(s\mid {\theta }^{\mu }\right)|}_{s=s_i}\right].\end{array}$$

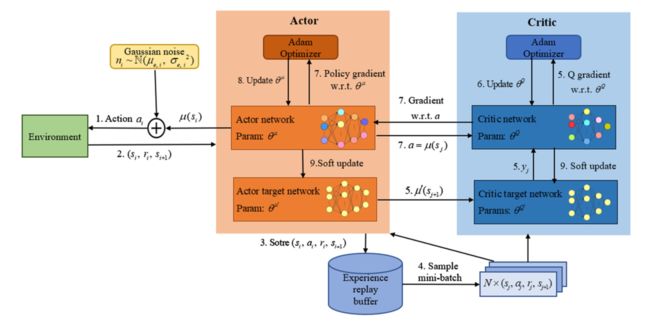
DDPG 算法的整个训练过程可以总结如下:首先，演员网络 $\mu$ 在上一个训练步骤之后输出 $\mu (s_i)$。**为了提供充分的状态空间探索，我们需要在探索和开发之间取得平衡。**实际上，我们可以将 DDPG 的探索与学习过程分开来看待，因为 DDPG 是一种 off-policy 算法。因此，我们通过添加行为噪声 $n_i$ 来构造动作空间，以获得动作 $a_i=\mu (s_i)+n_i$ ，其中 $n_i$ 服从高斯分布 $n_i\sim \mathbb{N}\left({\mu }_e,{\sigma }_{e,i}^2\right)$ ， ${\mu }_e$ 为平均值， ${\sigma }_{e,i}$ 是标准差。在环境中表演 $a_t$ 后，agent 可以观察到下一个状态 $s_{i+1}$ 和即时奖励 $r_t$。然后将元组 $\left(s_i,a_i,r_i,s_{i+1}\right)$ 存储在体验回放缓冲区中。之后，算法随机选择N个元组 $(s_j,a_j,r_j,s_{j+1})$ 在缓冲区中组成一个小批量，并将其输入演员网络和评论家网络。使用小批处理，演员目标网络 ${\mu }^{\prime }$ 将行为 ${\mu }^{\prime }(s_{j+1})$ 输出到评论目标网络 $Q^{\prime }$。利用 minibatch 和 ${\mu }^{\prime }(s_{j+1})$ ，批评家网络可以根据 $y_i=r_i+\gamma Q\left(s_{i+1},\mu \left(s_{i+1}\right)\mid {\theta }^Q\right)$ 计出目标值 $y_j$。

为了使损失函数最小化，批评家网络Q将由给定的优化器(如Adam optimizer)进行更新。然后，演员网络 $\mu$ 将小批量动作 $a=\mu (s_j)$ 发送给评论网络，以实现动作a的梯度 ${{\nabla }_{a}Q\left(s,a\mid {\theta }^Q\right)|}_{s=s_j,a=\mu \left(s_j\right)}$ 。参数 ${{\nabla }_{{\theta }^{\mu }}\mu \left(s\mid {\theta }^{\mu }\right)|}_{s=s_j}$ 可以由它自己的优化器导出。使用这两个梯度，参与者网络可以用以下近似更新:
$${\nabla }_{{\theta }^u}J\approx \frac{1}{N}\sum _j\left[{{{\nabla }_{a}Q\left(s,a\mid {\theta }^Q\right)|}_{s=s_j,a=\mu \left(s_j\mid {\theta }^{\mu }\right)}{\nabla }_{{\theta }^{\mu }}\mu \left(s\mid {\theta }^{\mu }\right)|}_{s=s_j}\right].$$
最后，DDPG agent使用小常数 $\tau$ 柔化更新批评家目标网络和行动者目标网络:
$$\begin{array}{l}{\theta }^{Q^{\prime }}\leftarrow {\theta }^Q+(1-\tau ){\theta }^{Q^{\prime }}\\ {\theta }^{{\mu }^{\prime }}\leftarrow {\theta }^{\mu }+(1-\tau ){\theta }^{{\mu }^{\prime }}\end{array}$$