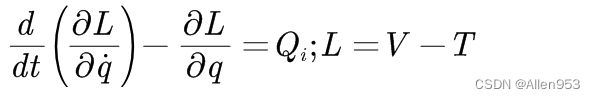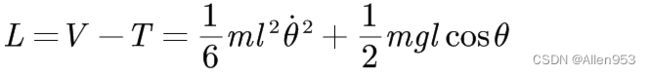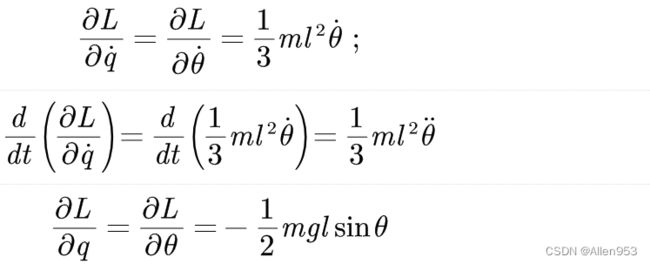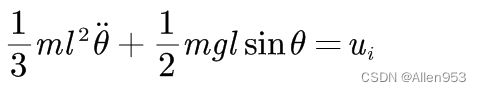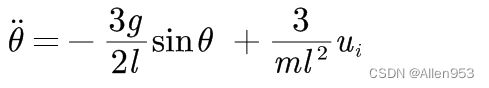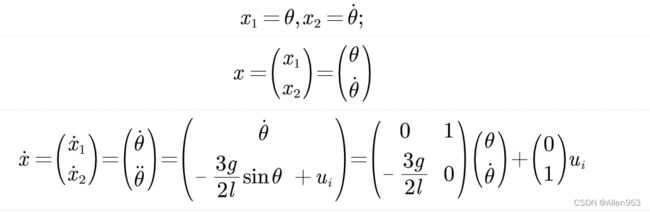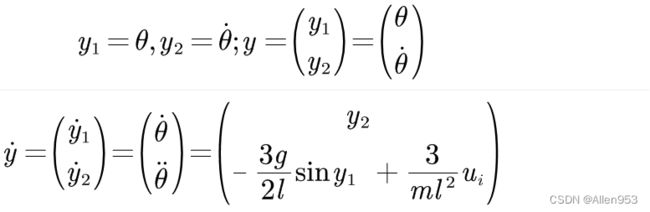单摆的动力学建模以及matlab仿真(牛顿法和拉格朗日方程法)
建模
牛顿法
有空再写
拉格朗日方程法
首先我们先确定广义坐标,并同时计算出来摆杆的转动惯量
接着列拉格朗日方程
计算动能(转动动能)
计算势能(取铰链处为零势能高度):
计算L
计算拉格朗日方程中的中间量
将上述的中间量带入拉格朗日方程,得到动力学模型:
变换一下形式:
当角度较小时
我们可以假设角度比较小,因为控制一般都是在平衡点附近。
当角度较大时
经常情况下角度没有那么小,这个时候我们就不能假设![]() ,所以就得到非线性的控制系统。
,所以就得到非线性的控制系统。
所以这个时候我们这样操作,将这个二阶微分方程转化成一阶微分方程组,这样就可以用matlab的ode45微分方程求解器求取数值解,求得的数值解即为系统状态 y。然后得到系统状态之后,控制器基于当前状态计算输入,再施加给执行器进行控制。
matlab仿真
我们先把微分方程求解器做出来:
直接把g=9.8,l=1和u=0带入式子;
[t,y] = ode45(@odeBai,[0 10],[1;0]);
plot(t,y(:,1),'-o',t,y(:,2),'-o');
function dy = odeBai(t,y)
dy = zeros(2,1);
dy(1) = y(2);
dy(2) = -3 * 9.8 / ( 2 * 1 )*sin(y(1))+0;
end从图片也可能看出规律:
这下,我们就求出来了位置(角度)时间曲线和速度(角速度)时间曲线。
然后,我们做一个控制器,把输入加上去。
控制器代码:
总程序代码:
clear all;
clc;
[t,y] = ode45(@odeBai,[0 10],[1;0]);
plot(t,y(:,1),'-o',t,y(:,2),'-o');
function dy = odeBai(t,y)
dy = zeros(2,1);
tau = PIDController(t,y);
dy(1) = y(2);
dy(2) = -3 * 9.8 / ( 2 * 1 )*sin(y(1)) + 3 * tau /(1*1*1);
end
function tau=PIDController(t,y)
% 目标状态
y1_desire = pi/4;
y2_desire = 0;
% 控制增益
Kp = 1000;
Kd = 500;
% 控制力矩
tau = Kp*(y1_desire-y(1))+Kd*(y2_desire-y(2));
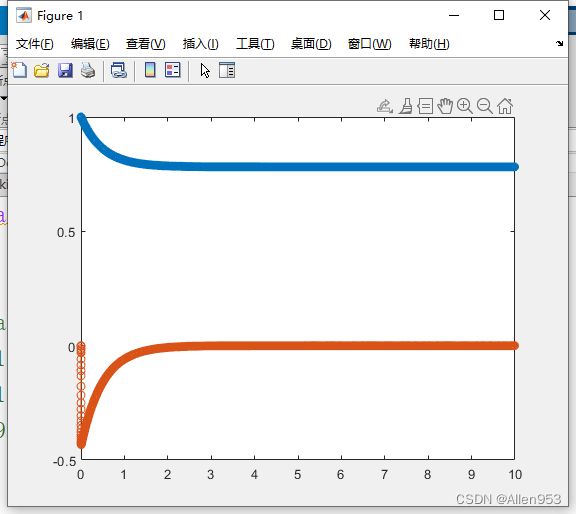
end 仿真图像如下:可以弹道蓝线逐渐逼近pi/4即45度的位置,而橙线从较大的值趋于0,即速度最终为0.
代码:
clear all;
clc;
global m l g
m = 1;
l = 1;
g = 9.8;
[t,y] = ode45(@odeBai,[0 10],[-1;0]);
figure(1);
plot(t,y(:,1),'-o',t,y(:,2),'-o');
figure(2);
x0=0;
y0=0;
v = VideoWriter('Pen.avi');
open(v);
for k=1:200:size(t)
x1=l*cos(y(k,1));
y1=l*sin(y(k,1));
link1_x=[0,x1];
link1_y=[0,y1];
line(link1_x,link1_y,'linewidth',2,'color','b')
axis equal
axis([-1.55 1.55 -1.55 0.55])
grid on;
hold on;
plot(x0,y0,'o','linewidth',2,'color','r');
frame = getframe(gcf);
writeVideo(v,frame);
clf;
end
close(v);
function dy = odeBai(t,y)
dy = zeros(2,1);
tau = PIDController(t,y);
dy(1) = y(2);
dy(2) = -3 * 9.8 / ( 2 * 1 )*sin(y(1)) + 3 * tau /(1*1*1);
end
function tau=PIDController(t,y)
% 目标状态
y1_desire = -pi/4;
y2_desire = 0;
% 控制增益
Kp = 1000;
Kd = 500;
% 控制力矩
tau = Kp*(y1_desire-y(1))+Kd*(y2_desire-y(2));
end
参考链接
1.matlab动力学建模与simscape验证(代码) - 哔哩哔哩