贝叶斯滤波详解

贝叶斯滤波

不熟悉贝叶斯的可以去看一下概率论4—条件概率 与 事件独立性

$P(B_i|A)=\frac{P(A{B}_i)}{P(A)}=\frac{P(A|B_i)P(B_i)}{{\sum }_{i=1}^{n}P(A|B_i)P(B_i)}$

贝叶斯公式 :

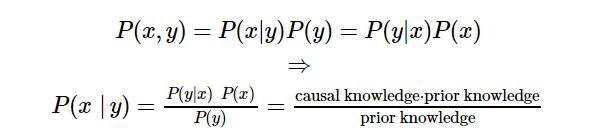
这个公式告诉我们可以由先验概率（prior knowledge），根据因果概率（causal knowledge）去估计后验概率。

或者说后验概率可以通过先验概率的不断修正得到，而这个修正就是通过利用因果概率进行的。
\qquad
举个例子： 设x事件为我偷吃烤鸭，y事件为我喝水
\qquad
我们容易知道两个事件没有必然联系，但是我们由常识（causal knowledge）知道我吃了烤鸭有40%的可能会渴的去喝水。
\qquad
现在问：你妈发现了你进厨房喝水了，你偷吃冰箱里的烤鸭概率有多大？

\qquad
你妈拿起笔，想：这小子平常几乎不出来喝水，一天出来喝水概率10%，以往买烤鸭的时候偷吃概率20%，而以往他吃完烤鸭有40%的概率出来喝水，拿起算盘就是一顿算：
\qquad \qquad $P(x|y)=\frac{P(y|x)P(x)}{P(y)}=0.4\ast 0.2/0.1=80$%

这小子这时候出来喝水，八成是偷吃冰箱烤鸭了，揍他！

看完上面的故事，我们容易知道，y通常是指一种观测事件，而x是你想推测的事件。

有了上面的故事，我们大概明白了，贝叶斯就是用来推测在观测到某些结果后，推测某个事件发生的概率。

再举个例子：
观测变量 y：机器人到门的距离，预测变量 x：门开着的概率
\qquad 问：机器人观测与门的距离为0.6m，门开着的概率是多少？

假设在观测状态为0.6m的情况下，以往经验而言，门开着的概率是P（x）=50%，并且统计以往的情况，门开着的情况下，机器人离门距离为0.6m的概率P（y|x）=P（y）=1。
\qquad $P(x|y)=\frac{P(y|x)P(x)}{P(y)}=1\ast 0.5/1=50$%
\qquad
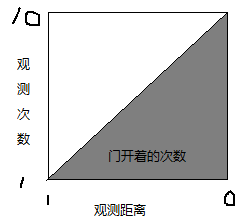
由于上述情况没有分辨率，是求某个状态下门开着的概率，比较简单，重新假设观测范围为0到1m，分辨率为0.1m，可令P（y）=0.1，假设以往经验而言，门开着的概率是P（x）=50%，并且统计以往的情况，门开着的情况下，机器人离门距离为0.6的概率P（y|x）=10%。
\qquad
\qquad $P(x|y)=\frac{P(y|x)P(x)}{P(y)}=0.1\ast 0.5/0.1=50$%
\qquad

你会说，我TM这是门禁系统，有人才开门，你告诉我50%几率撞门，你小子蒙我呢？
\qquad
这时候我脾气也上来了，你观测距离是0~1m，这时候门开着的概率必然是1，那你告诉我50%是个什么意思？是不是把观测距离是>1m的部分也全都算了进来？
\qquad
所以对于门禁系统，门开着的概率是P（x）=100%，所以$P(x|y)=\frac{P(y|x)P(x)}{P(y)}=0.1\ast 1/0.1=100$%
\qquad
这时候你想了想说，好像是这么个理儿，我现在把观测距离改成0~2m，在1—2m内门是关着的，门开着的概率是P（x）=50%了吧，你再给我算算看？
\qquad
重新假设现在观测分辨率为0.2m，P（y）还是=0.1门开着的概率是P（x）=50%，并且统计以往的情况，门开着的情况下，机器人离门距离为0.6的概率P（y|x）=20%。所以$P(x|y)=\frac{P(y|x)P(x)}{P(y)}=0.2\ast 0.5/0.1=100$%
\qquad
所以要注意研究样本是同一个时间点下对观测变量和预测变量进行同时采样，而不能是不同时间下的分别采样然后强行组合到一起，除非他们间隔时间非常短。

多变量观测与贝叶斯融合 :

上面的例子中，我们都是观测一个变量y，然后一个预测变量，现在我们采用两个观测变量（y，z）:

可得 $P(x|(y,z))=\frac{P(x\cap y\cap z)}{P(y\cap z)}$，根据概率学公式，可以继续推导：
\qquad
$\frac{P(x\cap y\cap z)}{P(y\cap z)}=\frac{P(y|(x\cap z))P(x|z)P(z)}{P(y|z)P(z)}=\frac{P(y|(x\cap z))P(x|z)}{P(y|z)}$
\qquad
上面的公式说明了一个问题，如果我们想求$P(x|(y,z))$，可以先求$P(x|z)$，这样对于多变量问题我们就可以通过递归来进行求解了。

当我们的观测变量$(z_1,....z_n)$达到了n个时，有：

$P(x|(z_1,z_2...z_n))=\frac{P(x\cap z_1...\cap z_n)}{P(z_1...\cap z_n)}$
根据上面的之前的推导，我们容易得出如下结论：
\qquad
$\frac{P(x\cap z_1...\cap z_n)}{P(z_1...\cap z_n)}=\frac{P(z_n|(x\cap z_1...\cap z_{n-1}))P(x|(z_1...\cap z_{n-1}))}{P(z_n|(z_1...\cap z_{n-1}))}$
\qquad
也就是说如果我们想求$P(x|(z_1...\cap z_n))$，可以先求$P(x|z_1...\cap z_{n-1})$，这样对于多变量问题我们就可以通过递归来进行求解了。
\qquad
我们令 ${\eta }_n=\frac{1}{P(z_n|(z_1...\cap z_{n-1}))}$
我们将公式改写成：
$P(x|(z_1,z_2...z_n))={\eta }_n\ast P(z_n|(x\cap z_1...\cap z_{n-1}))P(x|(z_1...\cap z_{n-1}))$
\qquad
由$Markov$(马尔可夫)属性，在$x$已知的情况下，$z_n$同$\{z_1,\dots ,z_{n-1}\}$无关，也就是独立的
所以实际上可以进一步简化：
$P(z_n|(x\cap z_1...\cap z_{n-1}))=\frac{P(x\cap z_1)...P(x\cap z_n)}{P(x\cap z_1)...P(x\cap z_{n-1})}=P(z_n|x)$
$P(z_n|(z_1...\cap z_{n-1}))=P(z_n)$
\qquad
（对于事件独立性不了解的可以看看概率论4—条件概率 与 事件独立性）
\qquad
最终贝叶斯递推公式变成：
$P(x|(z_1,z_2...z_n))={\eta }_n\ast P(z_n|x)\ast P(x|(z_1...\cap z_{n-1}))$
\qquad
如果继续对$P(x|(z_1...\cap z_{n-1}))$展开，我们可以得到：
$P(x|(z_1,z_2...z_n))=({\eta }_n\ast ..{\eta }_1)\ast (P(z_n|x)\ast ..P(z_1|x))\ast P(x)$
\qquad
即：
$P(x|(z_1,z_2...z_n))=P(x)\ast {\prod }_{i=1}^n[{\eta }_i\ast P(z_i|x)]$

我们继续沿用上面次那个机器人例子，假设我们现在连续观测三次，重新计算门开着的概率：

再举个例子：
观测变量 y：机器人到门的距离，预测变量 x：门开着的概率
\qquad 问：机器人观测三次，与门的距离分别为(0.6，0.5，0.5)m，门开着的概率是多少？


假设观测范围为0到1m，分辨率为0.1m，可令$P(y_i)=0.1$，假设以往经验而言，门开着的概率是$P(x)=55\%$，并且统计以往的情况，门开着的情况下，机器人离门距离为0.6概率为$P(y_i|x)=9\%$，且$P(y_i|\bar{x})=11\%$，机器人离门距离为0.5概率为$P(y_i|x)=10.9\%$，且$P(y_i|\bar{x})=8.9\%$，。
\qquad
$P(x|(y_1,y_2,y_3))=({\eta }_1\ast {\eta }_2\ast {\eta }_3)\ast (P(y_1|x)\ast P(y_2|x)\ast P(y_3|x))\ast P(x)$
要注意 ：
$P(y_3|x)中的x和P(y_2\mid x)的x$不一定是同一个东西，结果可能会出错，这样计算其实还存在一定的争议。
\qquad
其中${\eta }_3=\frac{1}{P(y_3)}=\frac{1}{0.1}$
但计算$P(x|(y_2,y_3))$时，${\eta }_2$就不能简单那么计算了：$y_2=(y_2\cap x)\cup (y_2\cap \bar{x})$，由于x是在y1之后的新x，
\qquad
即$P(y_2)=P(y_2\cap x)+P(y_2\cap \bar{x})=P(y_2|x)P(x|y_3)+P(y_2|\bar{x})P(\bar{x}|y_1)$
$P(y_1)=P(y_1\cap x)+P(y_1\cap \bar{x})=P(y_1|x)P(x|(y_2,y_3))+P(y_1|\bar{x})P(\bar{x}|(y_2,y_3))$
\qquad
计算：$P(x|y_3)={\eta }_3\ast P(x|y_3)\ast P(x)=\frac{0.09}{0.1}\ast 0.55=49.5\%;$
计算：$P(x|(y_2,y_3))={\eta }_2\ast P(y_2|x)\ast P(x|y_3)=\frac{0.109}{0.109\ast 0.495+0.089\ast 0.505}\ast 0.495=54.5\%$
计算：$P(x|(y_1,y_2,y_3))={\eta }_1\ast P(y_1|x)\ast P(x|(y_2,y_3))=\frac{0.109}{0.109\ast 0.545+0.089\ast 0.455}\ast 0.545=59.4\%$

我们可以看到如果三次观测，中，两次观测为0.5m，则可以提高门开着的置信程度

实际上，上面的用法还是存在问题的，
只要$P(y_i|x)>P(y_i\bar{x})$,我们就会发现利用$P(y_i)=P(y_i\cap x)+P(y_i\cap \bar{x})$计算后，有$P(y_i|x)>P(y_i)$,即:
$li{m}_{n\to \infty }P(x|(y_1,y_2,y_3,...y_n))=1$
\qquad
如果机器人一直停在$y_2$处观测，门开着的概率就变成$1$了？显然是不对的。
实际上，我们再

互补滤波器

举个例子，抛硬币：

拿一枚硬币，每第$i$次抛十次，结果记为$A_i$，事件$x$为硬币正面朝上，计算十次中正面的概率为$P(x|A_i)$，连续抛5次，我们应当有如下结果:
\qquad
$min\{P(x|A_i)\}\le P(x|A_i,A_2...A_n)\le max\{P(x|A_i)\}$
\qquad
假设5次抛硬币结果如下：
第一次 正面5个 ，$P(x|A_1)=50\%$
第二次 正面4个 ，$P(x|A_2)=40\%$
第三次 正面5个 ，$P(x|A_3)=50\%$
第四次 正面6个 ，$P(x|A_4)=60\%$
第五次 正面5个 ，$P(x|A_5)=50\%$
我们有：$min\{P(x|A_i)\}=40\%$，$max\{P(x|A_i)\}=60\%$，$P(x|A_i,A_2...A_5)=50\%$
\qquad
如果采用递归法，我们应该做如下更新：
$P(x|A_i,A_2)=P(x|A_2)\ast P(A_2)+P(x|A_1)\ast P(A_1)=45\%$
$P(x|A_i,A_2,A_3)=P(x|A_3)\ast P(A_3)+P(x|A_1,A_2)\ast P(A_1,A_2)=47\%$
$P(x|A_i,A_2,A_3,A_4)=....$
\qquad
我们在计算中，将上一次出现的概率假定为一个常数$\alpha$，表示上一次结果的可信度，如$\alpha =0.6$：
$P(x|A_i,A_2)=P(x|A_2)\ast (1-\alpha )+P(x|A_1)\ast (\alpha )=46\%$
$P(x|A_i,A_2,A_3)=P(x|A_3)\ast (1-\alpha )+P(x|A_1,A_2)\ast (\alpha )=47.6\%$
$P(x|A_i,A_2,A_3,A_4)=....=52.5\%$
$P(x|A_i,A_2,A_3,A_4,A_5)=....=51.5\%$

我们能够看到，虽然结果不那么准确，但是和真实结果误差非常小，且计算简单。对于连续观测滤波，效果非常好，甚至对于传感器融合，效果也很好。

卡尔曼滤波

机器人中的贝叶斯滤波

给定一个概率函数$P(x_t,u_t,z_t)$，其中$x_t$是状态轨迹，时间从0到$t$，$z_t$是观测轨迹， 从时间1到$t$，$u_t$是动作轨迹，从时间1到$t$。

两个核心

再介绍这两部分之前，我们首先来看如下形式的关系如何推导：

1、$P(x_t|u_t)$

公式：$P(A)={\sum }_{B}P(AB)$
\qquad
$P(x_1|u_1)=\frac{P(x_1,u_1)}{P(u_1)}={\sum }_{x_0}\frac{P(x_1,u_1,x_0)}{P(u_1)}={\sum }_{x_0}P(x_0)P(x_1|u_1,x_0)$
\qquad
这个公式的意义是：
对于在条件动作是u1情况下，状态为x1的概率是所有x0状态下的概率乘以转移到x1状态的概率的加和。
\qquad
如果说x是单变量，那它的概率就是普通概率，如果x是多变量，那就涉及状态转移矩阵了，这部分就涉及离散动力系统，马尔可夫什么的就出来了。

2、$P(x_t|u_t,z_t)$

考虑两点：z1和当前状态x1的关系、如何使用之前推导的p(x1|u1)
\qquad
$P(x_1|u_1,z_1)=\frac{P(x_1,u_1,z_1)}{P(u_1,z_1)}=\frac{P(z_t|x_1,u_1)P(x_1,u_1)}{P(u_1,z_1)}$
\qquad
$=\frac{P(z_t|x_1,u_1)P(x_1,u_1)}{{\sum }_{x_1}P(x_1,u_1,z_1)}$
\qquad
$=\frac{P(z_t|x_1,u_1)P(x_1|u_1)P(u_1)}{{\sum }_{x_1}P(z_1|x_1,u_1)P(u_1,x_1)}$
\qquad
$=\frac{P(z_t|x_1,u_1)P(x_1|u_1)P(u_1)}{{\sum }_{x_1}P(z_1|x_1,u_1)P(x_1|u_1)P(u_1)}$
\qquad
$=\frac{P(z_t|x_1,u_1)P(x_1|u_1)}{{\sum }_{x_1}P(z_1|x_1,u_1)P(x_1|u_1)}$
\qquad
这个公式中：
上半部分对于每一个在初始状态x0，做了动作u1，状态转移到状态x1 并且在x1状态下得到观测值z1的概率；
下半部分是对于每一个当前可能的状态x1的值，p(x1|u1)概率乘以在x1下获得观测z1的加和。

预测

预测部分就是: 根据在历史动作$\{u_1,u_2...u_{t-1}\}$下产生的观测轨迹$\{z_1,z_2...z_{t-1}\}$，以及当前最新动作$u_t$，预测最新的状态$x_t$，简记 $P(x_t|u_{1:t}，z_{1:t-1})$，我们可以推导出：

$P(x_t|u_{1:t}，z_{1:t-1})={\sum }_{x_{t-1}}P(x_t,x_{t-1}|u_{1:t},z_{1:t-1})$
\qquad
$={\sum }_{x_{t-1}}P(x_t,x_{t-1}|u_t,u_{1:t-1},z_{1:t-1})$
\qquad
$={\sum }_{x_{t-1}}P(x_t|x_{t-1},u_t)P(x_{t-1}|u_{1:t-1},z_{1:t-1})$

修正

修正部分就是：根据最新观测量$z_t$，对预测的最新状态$x_t$进行修正，简记 $P(x_t|u_{1:t}，z_{1:t})$，我们可以推导出：

$P(x_t|u_{1:t}，z_{1:t})=\frac{P(x_t,u_{1:t},z_t,z_{1:t-1})}{P(u_{1:t},z_t,z_{1:t-1})}$
\qquad
$=\frac{P(z_t|x_t,u_{1:t},z_{1:t-1})P(x_t,u_{1:t},z_{1:t-1})}{P(z_t|u_{1:t},z_{1:t-1})P(u_{1:t},z_{1:t-1})}$
\qquad
$=\frac{P(z_t|x_t,u_{1:t},z_{1:t-1})P(x_t|u_{1:t-1},z_{1:t-1})}{P(z_t|u_{1:t},z_{1:t-1})}$
分母$P(zt|z1:t-1,u1:t)$这项没有什么意义（现在的测量值和现在的位置有关系，与之前的测量值没什么关系），所以把它作为一个归一化参数比如n，所以$P(z_t|x_t,u_{1:t},z_{1:t-1})=P(z_t|x_t)$
\qquad
$P(x_t|u_{1:t}，z_{1:t})=\frac{P(z_t|x_t)P(x_t|u_{1:t-1},z_{1:t-1})}{P(z_t|u_{1:t},z_{1:t-1})}$
\qquad
$=\frac{P(z_t|x_t,)P(x_t|u_{1:t-1},z_{1:t-1})}{{\sum }_{x_t}P(z_t,x_t|u_{1:t},z_{1:t-1})}$
\qquad
$=\frac{P(z_t|x_t,)P(x_t|u_{1:t-1},z_{1:t-1})}{{\sum }_{x_t}P(z_t|x_t)P(x_t|u_{1:t},z_{1:t-1})}$

算法总结