knowledge graph embedding---Trans全家桶
知识图谱(knowledge graph)是一种具有多种节点类型和多种连接关系的网络,因为其可以表示现实世界中丰富的关系而得到重视,从知识图谱中挖掘出有用的信息称为研究的一个热点。但是目前绝大多数数据挖掘的方法处理的输入都是向量空间,无法在图上进行数据挖掘,因此,将图的节点与关系使用向量的形式表示——这就是embedding的含义。图经过embedding之后,可以使用很成熟的数据挖掘方法进行处理。把图空间映射到向量空间的这个过程叫做图的表示学习。下图就是将网络中的节点嵌入到一个二维的向量中,从而使用经典机器学习方法进行聚类:
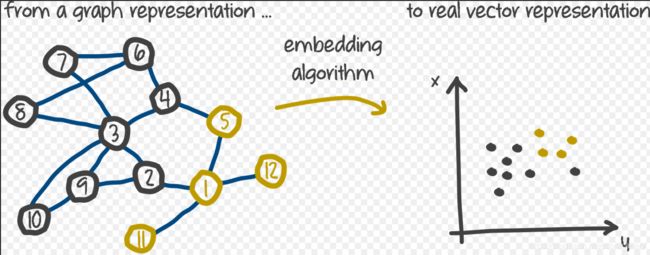
下面我将介绍几种知识图谱经典嵌入模型:
1.TransE
Translating embeddings for modeling multi-relational data.Bordes A, Usunier N, Weston J, et al. NIPS. 2013.
我们使用三元组 ( h , l , t ) (h,l,t) (h,l,t)来表示知识图谱中的一个关系,TransE的目的是为知识图谱中的每一个实体与关系训练一个嵌入表示,使得 h + l ≈ t h+l\approx t h+l≈t。而对于不存在知识图谱中的关系 ( h , l , t ′ ) (h,l,t') (h,l,t′),我们使得 h + l h+l h+l与 t ′ t' t′之间的距离尽可能地远。
TransE模型训练简单快速,可以适用于大规模数据的训练,但是无法处理一对多或者多对一的关系。这个很好理解,因为对于知识图谱中的两个关系 ( h , l , t 1 ) (h,l,t1) (h,l,t1)和 ( h , l , t 2 ) (h,l,t2) (h,l,t2),我们经过TransE训练之后会得到 t 1 ≈ t 2 t1 \approx t2 t1≈t2。

- TransH
Zhang J . Knowledge Graph Embedding by Translating on Hyperplanes[J]. AAAI - Association for the Advancement of Artificial Intelligence, 2015.

在上面我们讲到,TransE的缺点是不能很好地处理多对一或者一对多的情况,那么我们就讲到TransH对这种情况的处理方式。
如上图所示,平行四边形代表着一个关系r的超平面,对于任意 ( h , r , t ) (h,r,t) (h,r,t),我们首先得到 h , t h,t h,t在超平面上的投影 h ⊥ , t ⊥ h_⊥,t_⊥ h⊥,t⊥,我们训练的优化目标是尽量让 h ⊥ + r = t ⊥ h_⊥+r=t_⊥ h⊥+r=t⊥。这样一来,即使在KG中出现两个关系 ( h 1 , r , t ) , ( h 2 , r , t ) (h_1,r,t),(h_2,r,t) (h1,r,t),(h2,r,t),我们也不需要使得 h 1 = h 2 h_1=h_2 h1=h2,而只需要让他们俩在超平面上的投影 h 1 ⊥ = h 2 ⊥ h_{1⊥}=h_{2⊥} h1⊥=h2⊥。
- TransR
Yankai Lin, Zhiyuan Liu, Maosong Sun, Yang Liu, and Xuan Zhu. 2015. Learning entity and relation embeddings for knowledge graph completion. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence (AAAI’15). AAAI Press, 2181–2187.
TransE和TransH的一个相同的问题就是其假设实体和关系都处于同一向量空间内(都是k维),TransR就很好地解决了这个问题,其假设实体的嵌入为k维,而关系的嵌入为d维。为每个关系r定义一个转化矩阵 M r ∈ R k ∗ d M_r∈R^{k*d} Mr∈Rk∗d,对于一个关系 ( h , r , t ) (h,r,t) (h,r,t),那么我们优化的目标就是
l o s s = ∣ ∣ h M r + r − t M r ∣ ∣ loss=||hM_r+r-tM_r|| loss=∣∣hMr+r−tMr∣∣
作者还给出了一个CTransR模型,其思想如下:
对于知识图谱中的同一个关系 r r r,其对于不同的 ( h , t ) (h,t) (h,t)所表示的含义也是不同的,比如说对于三元组模式 ( l o c a t i o n − c o n t a i n − l o c a t i o n ) (location-contain-location) (location−contain−location),其包含 c o u n t r y − c o n t a i n − c i t y , c o u n t r y − c o n t a i n − u n i v e r s i t y , c o n t i n e n t − c o n t a i n − c o u n t r y country-contain-city,country-contain-university,continent-contain-country country−contain−city,country−contain−university,continent−contain−country等类型的实体,对于着其中的每一种实体,我们希望使用不同的 M r M_r Mr将 h , t h,t h,t映射到同一空间,因此对于一个关系 r r r,我们首先将被这个关系 r r r所连接的 ( h , t ) (h,t) (h,t)进行聚类,为每一类训练一个 M r M_r Mr进行投影操作。
TransR的好处是为保证了实体向量和关系向量不处于同一空间,但是因为引入了矩阵运算,不能适用于大规模知识图谱上。关于同一关系对不同实体的影响不同的考虑上,TransR引出了CTransR,但是CTransR操作又进一步提高了计算的复杂度。
- TransD
Ji G , He S , Xu L , et al. Knowledge Graph Embedding via Dynamic Mapping Matrix[C]// Meeting of the Association for Computational Linguistics & the International Joint Conference on Natural Language Processing. 2015.
我们在上一节中说到TransR需要为每一个关系保存一个矩阵,训练开销非常大,这一节中的TransD就解决了这样的问题:
对于KG中的一个关系 ( h , r , t ) (h,r,t) (h,r,t),我们为其中的实体和关系都保存两个向量,一个向量是embedding,另一个向量用来构造映射矩阵。也就是说,我们保存 ( h , h p , r , r p , l , l p ) (h,h_p,r,r_p,l,l_p) (h,hp,r,rp,l,lp),其中 h , h p , l , l p ∈ R n , r , r p ∈ R m h,h_p,l,l_p∈R^n,r,r_p∈R^m h,hp,l,lp∈Rn,r,rp∈Rm。
与TransH,TransR相似,我们需要将 h , t h,t h,t映射到 r r r的空间中,然后最小化损失,那么我们首先构造映射矩阵:
M r h = r p h p T + I m × n M_{rh}=r_ph_p^T+I^{m×n} Mrh=rphpT+Im×n
M r t = r p t p T + I m × n M_{rt}=r_pt_p^T+I^{m×n} Mrt=rptpT+Im×n
然后我们使用映射矩阵将 h , t h,t h,t映射到 r r r的空间中:
h ⊥ = M r h h , t ⊥ = M r t t h_⊥=M_{rh}h,t_⊥=M_{rt}t h⊥=Mrhh,t⊥=Mrtt
损失函数定义为:
f r ( h , t ) = − ∣ ∣ h ⊥ + r − t ⊥ ∣ ∣ 2 2 f_r(h,t)=-||h_⊥+r-t_⊥||_2^2 fr(h,t)=−∣∣h⊥+r−t⊥∣∣22
也就是说尽量使得投影之后的 h h h加上 r r r等于投影之后的 r r r。
在矩阵相乘方面,TRansD使用了接下来的trick避免了TransR中矩阵和向量的相乘:

TransD使用动态构造矩阵的方法,加速了模型的训练,同时由于为每个实体与关系构造专属的映射矩阵,增加了模型的准确度,是一种非常成功的embedding方法。
2021.09.10更新
其实回过头来看Trans系列的模型,更多的是一种“生成”思想。如果说GCN是根据图来生成embedding的话,Trans的目标是在给定embedding的情况下,使得生成这个图的概率最大,因此对于图中真实存在的边,我们在损失函数中给出奖励,对于不存在的边,我们给出惩罚。