目标检测之YOLOv4算法分析

基本原理

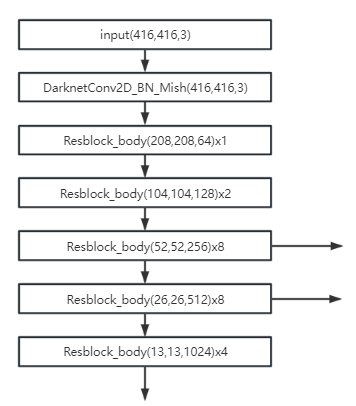
网络结构

CSPDarknet53

最后三个箭头指向输出即三种特征图

SPP
解决多尺度问题
对于同一个特征输出图，进行三种maxpool2d操作，然后将三种操作的输出进行叠加

PANet
融合上采样、下采样等特征，深度方向拼接

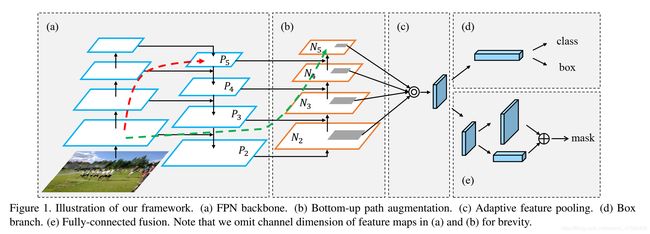
PANet由五个核心模块组成（a,b,c,d,e）

图中红色和绿色的虚线是跨越多层的shortcut，更高实现不同层次的特征融合。

图a中为FPN的自上而下结构，第一列的4个特征图为依次卷积的结果，浅层反应边缘等细节，深层反应更丰富语义特征，第二列为4组feature map,分别为$P_5,P_4,P_3,P_2$，上采样过程使用双线性插值方式。为何不直接使用第一列的特征图旨在单独使用每一层的特征图无法反映整体特征，会减弱表达能力；而使用第二列的特征，可以将浅层特征与深层特征进行融合，达到更为丰富的表达特征。

图b中为自下而上的路径，得到$N_2,N_3,N_4,N_5$共4个feature map.其中$N_2$就是复制$P_2$,$N_3$是通过将$N_2$经过步长为2的$3\ast 3$卷积后的结果加上$P_3$得到的，其他一样处理。

图c为自适应特征池化，融合所有层的feature map，最后得到一个$1\ast 1\ast n$的向量，用于分类与定位

损失函数

$$\begin{gathered} Loss={\lambda }_{coord}\sum _{i=0}^{S^2}\sum _{j=0}^M{I}_{ij}^{obj}(2-w_i\ast h_i)(1-CIOU) \\ -\sum _{i=0}^{S^2}\sum _{j=0}^M{I}_{ij}^{obj}[\widehat{C_i}log(C_i)+(1-\widehat{C_i})log(1-C_i)] \\ -{\lambda }_{noobj}\sum _{i=0}^{S^2}\sum _{j=0}^M{I}_{ij}^{noobj}[\widehat{C_i}log(C_i)+(1-\widehat{C_i})log(1-C_i)] \\ -\sum _{i=0}^{S^2}\sum _{j=0}^M{I}_{ij}^{obj}\sum _{cϵclasses}[\widehat{p_i}(c)log(p_i(c))+(1-\widehat{p_i}(c))log(1-p_i(c))] \end{gathered}$$
第一行为正样本的坐标损失，$2-w_i\ast h_i$为惩罚系数，$CIOU$损失为在DIOU基础上增加的尺度损失。计算公式为
$$\begin{gathered} CIOU=IOU-(\frac{{\rho }^2(b,b^{gt})}{c^2}+\alpha \nu ) \\ \nu =\frac{4}{\pi }(arctan\frac{w^{gt}}{h^{gt}}-arctan\frac{w}{h}{)}^2 \\ \alpha =\frac{\nu }{(1-IOU)+\nu } \end{gathered}$$
其中$b$代表预测中心坐标，$b^{gt}$代表真实框中心坐标；$\rho$代表$b$和$b^{gt}$之间的欧氏距离；$c$代表预测框与真实框最小外接矩形对角线长度；$w、h$和$w^{gt}、h^{gt}$分别代表预测框和真实框的宽、高；
第二行为正样本的置信度损失
第三行为负样本的置信度损失
第四行为分类损失

---

优化方案

边界框回归

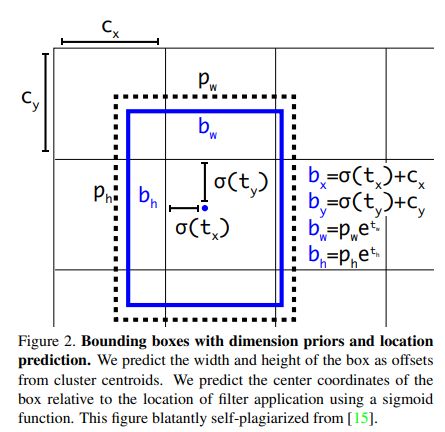
在yolov2和yolov3中都使用边界框回归的方案，预测$t_x,t_y,t_w,t_h$四个与预测框位置和大小相关的参数，而在yolov4中沿用该方法，但采取一点优化：
原方法使用sigmoid函数限制$t_x,t_y,t_w,t_h$这四个值在(0,1)之间。
由于$$\sigma (x)=\frac{1}{1+e^{-x}}$$

值域在$（0，1）$之间，那么导致在基准点$(c_x,c_y)$基础上，偏移量为$(0,1)$，那么预测框的中心点只能在grid cell格子内部。
此时，存在一种特殊情况，若真实框的中心点落在grid cell的边界线上，如$(c_x,c_y)$位置，那么预测框的中心位置也在$(c_x,c_y)$将会是最好的效果，到达此条件，就要求公式中$\sigma (t_x)=0,\sigma (t_y)=0$.但对于sigmoid函数而言，实现等于0的条件为x趋近于负无穷时，函数值为0。这种情况对于网络而言，难以实现。
为此，在yolov4中，引入缩放因子$scal{e}_{xy}$,数学计算公式为
$$\begin{gathered} b_x=(\sigma (t_x)\ast scal{e}_{xy}-\frac{scal{e}_{xy}-1}{2})+c_x \\ {b}_y=(\sigma (t_y)\ast scal{e}_{xy}-\frac{scal{e}_{xy}-1}{2})+c_y \end{gathered}$$
在实际使用中，$scal{e}_{xy}$常取值为2，则原计算式为
$$\begin{gathered} b_x=(\sigma (t_x)\ast 2-0.5)+c_x \\ {b}_y=(\sigma (t_y)\ast 2-0.5)+c_y \end{gathered}$$
即在原$\sigma (x)$乘以2，表达式为$$\sigma (x)=\frac{2}{1+e^{-x}}$$

$$\sigma (x)=\frac{2}{1+e^{-x}}-2$$

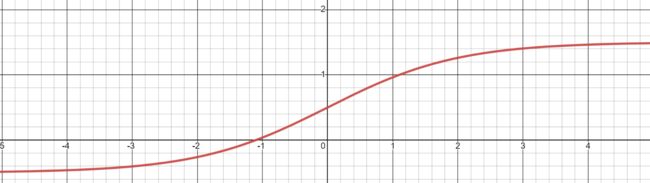
从上图可知值域变为$(-0.5,1.5)$
那么最后得到的预测框的中心位置可以在偏离grid cell内部一定距离，如x坐标在$(c_x-0.5,c_x+1.5)$之间,y坐标在$(c_y-0.5,c_y+1.5)$之间，那么即使真实框的中心在边界线上也无关紧要了。

Mosaic 数据增强

mosaic是通过混合4张训练图像的数据增强方式，使模型具有更好的鲁棒性。

IOU阈值处理
对于每一个grid cell的anchor,若存在多个anchor与真实框的IOU值大于阈值，则令这几个anchor都进行预测，可以增加正样本数量。

具体实现方法为：

将每一个anchor与真实框左上角对齐，计算IOU值。

如上图，若对于某个真实框，中心点在深绿grid cell中，那么深绿grid cell生成的anchor中与真实框IOU最大（并且满足阈值）的anchor肯定是正样本，但不仅仅这一种正样本。对于深绿框左侧与上侧两个grid cell生成的anchor中，满足阈值的anchor也会作为该真实框的正样本，之所以这样做，可结合上面对边界框优化那一部分理解，由于偏移量在$(-0.5,1.5)$之间，那么预测框的中心点位置是可能出现在左侧与上侧的。我们进行回归的目的在于使预测框与真实框更加接近，那么在优化之后，就有更多的预测框可以优化接近于真实框，使预测效果更好。