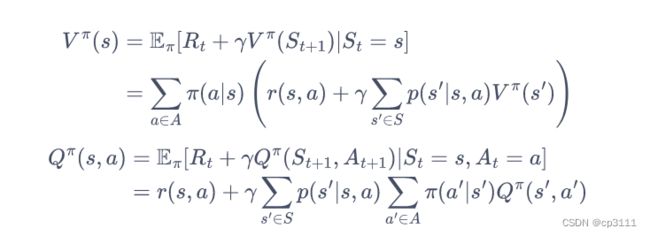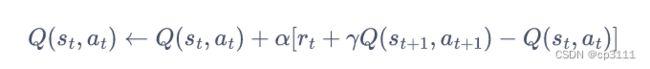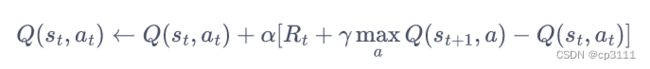强化学习笔记（初级篇）

刚看完李伟楠老师的《动手学强化学习》中强化学习基础篇，写一篇博客记录一下学习内容和学习心得。关于机器学习，之前在校内上过深度学习基础课程，对于深度学习有一个基础性的了解，由于是选修课，没有做大量作业，对于知识的理解一般化。目前做的方向是基于强化学习的路径规划，所以要先把强化学习的基础过一遍。想把强化学习的一些基础问题和概念记录一下。

第一个问题，什么是强化学习？

强化学习是智能体通过和环境进行交互来实现目标的一种计算方法。一轮交互是指，智能体在当前状态S，采取动作A，作用给环境以后，智能体会得到一个来自环境的奖励R以及智能体的下一个状态S'，这种交互方式是迭代进行的。

智能体的三个要素：感知、决策、奖励。

感知：就是智能体要感受到自己所处于一个什么样的状态。

决策：在这个状态下，要采取一个什么样的动作来达到目标。

奖励：在状态下采取动作所获得的奖励。智能体的目标就是最大化在多轮交互中累积奖励的期望。

环境：

通常认为一个环境是动态的，也可以认为是一个随机过程，最重要的两个因素就是状态以及状态的转移概率，当这个环境收到了干扰以后（即智能体的动作），状态转移概率就取决于环境和智能体动作共同决定的。其中，智能体采取的动作是随机的，环境基于当前状态以及智能体的动作下一时刻的状态也是随机的。（智能体采取动作的随机性是指：比如策略是，环境的随机性是指比如在S,A下有0.2的概率转移到S1,0.8的概率转移到S2）。

强化学习中的一些基本定义：

马尔可夫过程：

具有马尔可夫性质的随机过程。马尔可夫性质：P(St+1|St, St-1,...,S1) = P(St+1|St),即下一时刻的状态只当前时刻的状态决定。并不是说和以前的状态无关，因为现在的状态和上一时刻有关，是迭代过来的，以前时刻的状态信息传递到了当前状态。

回报：

,奖励衰减的累积和其中Rt是t时刻状态的奖励，是衰减因为，取值范围是（0,1）代表对未来回报的一个衡量，越大代表越看重未来的奖励。

价值：

一个状态的期望回报定义为这个状态价值，所有状态的价值就组成了价值函数V(s).

V(s) = E(Gt | St = s) .

上式经过推导我们可以得到Bellman方程，推导过程如下：

贝尔曼方程（Bellman equation）：

 

 策略：

,用来表示策略，意思是在状态s下采取动作a的一个概率分布。这个策略可以是一个确定性的策略，也可以是一个不确定的策略。当它是一个确定性的策略时，那么它在状态s下采取动作a的概率为1，其他动作为0。当它是不确定性策略时，那么状态s下动作a就是一个概率分布。

状态价值函数：

,表示从状态s开始遵循策略所获得的回报的期望。

动作价值函数：

,表示在状态s采取动作a遵循策略所获得的回报的期望。

经过推导我们可以知道状态价值函数和动作价值函数的关系：

 

贝尔曼期望方程：

通过推导得到两个价值函数的贝尔曼期望方程：

算法：

根据环境已知和未知，我们可以采用不同的算法去求解。当环境已知的时候，即奖励函数和状态转移概率已知。

这种情况我们采取动态规划算法，又分为策略迭代算法和价值迭代算法。就不需要通过和环境进行大量的交换而直接进行规划。

动态规划算法：

策略迭代算法：

首先会初始化一个策略。

主要是不停地循环两个过程：策略评估和策略更新

策略评估：根据当前的策略，计算出状态价值函数；

策略更新：根据状态价值函数，贪心的在每一个状态选择动作价值最大的动作。

然后重复进行以上两个过程。

价值迭代算法：

对于每个状态，初始化V(s) = 0。

只维护一个状态价值函数：

对于每一个状态更新：

最后策略恢复就是在每个状态s采取动作a使得状态价值最大。

当环境模型未知的时候，即奖励函数和状态转移矩阵未知，可以通过采样得到的数据进行数据学习，称为无模型的强化学习，我们可以采取如下算法：

1.蒙特卡洛采样法

2.时序差分法

蒙特卡洛

当我们不知道奖励函数和状态转移矩阵的时候，就没有办法直接去计算价值函数，因此我们采取的办法是去估计价值函数，如何估计呢？

采取抽样的方法，根据策略在MDP采样很多序列，然后对于每条序列出现的每一个状态出发的回报，再求其期望就是价值。对于每一个序列的每一个时间步t的状态s进行以下操作：

1.更新计数器N(s) = N(s) +1;

2.G(s) = G(s) + Gt;

最后V(s) = G(s) / N(s);

还有一种增量式的更新方法：V(s) <-- V(s) + a(Gt - V(s))

时序差分算法

是一种用来估计策略的价值函数方法，结合了蒙特卡洛和动态规划算法的思想。和蒙特卡洛的相似之处在于也是用过采样的数据进行学习，和动态规划的相似之处在于都是通过贝尔曼方程思想，利用后续状态价值来更新当前状态价值。

蒙特卡洛的更新要等到这个序列结束之后才可以进行更新，而时间差分的算法只要当前步结束就可以进行计算。即用当前状态动作的奖励和下一状态的价值估计作为当前状态的回报。

这里就有两个算法：

1.Sarsa算法

在线策略。采用的策略，用同一个策略来获取经验，并且更新数据。获得的数据元组是{s,a,r,s',a'}

 

2.Q-learning

这应该是最有名的一个算法了，是离线策略。获得数据遵循的策略是行为策略获得{s,a,r,s'}数据元组,a'的动作是根据目标策略所做出的动作，一般行为策略是，目标策略是Greedy策略。

 基于模型的强化学习这里就省略了，它的思想就是根据经验建立相应的环境模型，由于这个模型本身就是有误差的，所以这个模型的好坏很重要，有了模型以后，我们就可以减少与环境进行交互的次数，而多次和模型进行交互，这样的好处是因为强化学习算法有一个指标是样本的数量，样本越少说明这个算法效率就高，比较经典的算法是Dyna-Q。想要了解可以看动手强化学习这本书的第六章。

---

后面还会更新强化学习进阶篇的内容。有什么错误欢迎批评指正，有什么问题欢迎交流。对于这本书的配套资料还是建议先看一遍书，再去看对应的视频，视频的顺序不是按照书上的顺序来的，但是内容都有。