强化学习笔记

本文（不断更新）是学习以下课程/文献的笔记：

• 课程：UCL Cource on RL http://www0.cs.ucl.ac.uk/staff/D.Silver/web/Teaching.html
• 课程：Berkeley cs188 http://inst.eecs.berkeley.edu/~cs188/fa18/
• 书籍：Reinforcement learning: An Introduction https://web.stanford.edu/class/psych209/Readings/SuttonBartoIPRLBook2ndEd.pdf

1. 强化学习是什么

强化学习是机器学习的一种，它要解决的是“在某种状态下，应该做什么”的时序决策（sequential decision making）问题。
强化学习和监督学习的差别在于：监督学习需要利用标注数据集进行训练，训练出一个模型后在进行判断；强化学习也要训练，但不需要标注数据集，而是通过不断“尝试-试错”的模式进行学习。
对于一个智能体（agent）来说，它要在环境（environment）中达到某种目标。为了达到目标，它会观察到环境中的某些信息，然后做出某项动作（action），这个动作会作用到环境中，然后环境会给智能体一个激励/奖赏（reward）：智能体做出正确的动作则有正奖赏，反之则是负奖赏（即惩罚）。智能体就是在这种奖赏机制下学到正确的动作，即为强化学习。

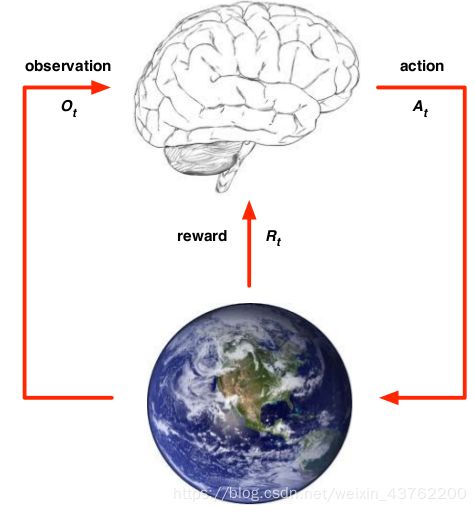
强化学习的几个要素

• 状态（state）
  状态可以理解为关于agent和环境的信息，比如某个地点、agent所处的位置、agent自身的速度等。状态是需要agent去获取的。因为强化学习是一个时序决策的问题，即存在$S_0$, $S_1$,…$S_t$, $S_{t+1}$个状态，如果”下一个状态只与当前状态有关，而与更早之前的状态无关”， 即条件概率满足：
  $$P(S_{t+1}|S_t)=P(S_{t+1}|S_t,S_{t-1},...,S_0)$$
  那么我们说该问题具有马尔科夫性，我们的强化学习问题也变成马尔科夫决策问题（MDP）.
• 动作（action）
  即agent的动作
• 策略（policy）
  策略就是状态到动作的映射：处在某一状态下应该做什么动作
• 目标（goal）
  在一个问题中agent要达到的目标，比如是从迷宫中达到出口。目标可以用激励来量化表示
• 激励（reward）
  这是环境给agent的反馈，agent的终极目标就是要把累积的reward最大化. 需要注意的是，当下行为会得到一个即时的reward，但其真正的价值，可能要等到一定时间后才体现，正所谓“不是不报，时候未到”
• 值函数（value function）
  激励表示对动作的即时奖惩，而值函数表示某个策略的终极价值

2. Markov Decision Process (MDP)

强化学习往往可以由马尔科夫决策过程（MDP）来描述。MDP是一个时序问题，在每个时刻$t$它都被这样一个元组 $⟨S,A,P,R,\gamma ⟩$所定义, 其中：

• $S$ 为有限的state组成的状态空间
• $A$ 为有限的action组成的动作空间
• $P$ 是状态转移概率矩阵，即在状态$s$时，采取$a$动作，状态转移到$s^{\prime }$的概率：
  $$P_{s,s^{\prime }}^a=P[S_{t+1}=s^{\prime }|S_t=s,A=a]$$
  为什么从一个状态到另一个状态是概率性的呢？例如一个机器人在A点（$s$）决定采取动作"跳"转移到B点（$s^{\prime }$），但由于控制的bug等原因，它有可能只有90%的可能性成功到达B点，而有10%的可能性停留在A点。
• $R$ 是激励函数，即在状态$s$时，采取$a$动作，能够得到的期望奖励（任何实数）：
  $$R_s^a=\mathbb{E}[R_{t+1}|S_t=s,A=a]$$
  这个奖励跟$t+1$时刻的状态没关系，比如上面说的机器人，只要它在A点采取“跳”这个动作了，那么就会有一个奖励。
• $\gamma$ 是discount factor，这个是用来表述总回报（returns）$G_t$的：
  $$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...=\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1},(\gamma \in [0,1])$$
  从$t$时刻开始，之后的每个$t+k+1$时刻会有激励$R_{t+k+1}$，但是总的回报不是所有$R_{t+k+1}$的直接加和，而是会把离$t$越远的的激励discount掉越多、再加和，这么做有两个理由：一是，这比较符合生物智能的特点——一般生物都是考虑眼前好处，而缺乏长远目光；二是数学上有助于后面我们求解收敛，因为：
  $$\begin{array}{rl}{G}_t& =R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...\\ & \le R_{max}\sum _{k=0}^{\infty }{\gamma }^k\\ & =\frac{R_{max}}{1-\gamma }\end{array}$$
  只要$\gamma$ 小于1，回报$G_t$,是收敛的，即使时间无限长。

下图是一个MDP的例子：每个圆圈或者正方形表示一个状态；每个红色字体表示一个动作，每个箭头表示采取该动作将使状态转移；每个R表示激励

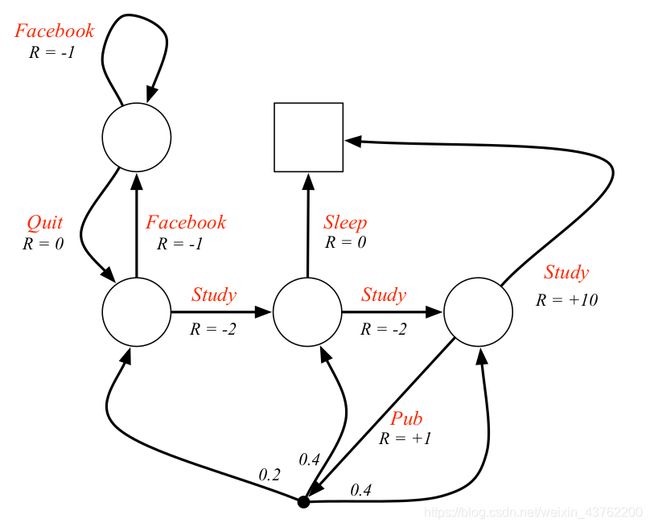
在MDP中，智能体从一个状态转移到另一个状态，上面说了可以由转移概率分布来描述，而实际上这种转移由具体动作来实现。在某个状态时采取某种行动，我们称之为策略（policy），记为$\pi$:
$$\pi (a|s)=Prob[A_t=a|S_t=s]$$
$\pi$是一个概率分布，就是说某个状态下有可能采取不同的动作。考虑下面这个状态转移例子：空心圆圈表示状态，实心黑点表示动作。从最上面的状态$s$出发，我们有一定的概率分布$\pi$可以采取3种不同的动作$a$. 而采取某一个动作后，我们即会获得激励$r$, 并且有一定转移概率$p$会使状态转移到下一个$s^{\prime }$. 本例子中最下层空心圆圈表示，某个动作后都有两种新的状态的可能性。

2.1 状态值函数（state value function）

好了，现在在MDP中，状态之间可以通过策略函数$\pi$和转移函数$P$函数联系起来。并且，在某一个状态采取某一动作时，智能体会得到一个激励（不管是正的还是负的）。我们说强化学习的终极目标是获得最大化的累积的激励，而不是当下的激励；有可能这一步走出去捡到个宝，获得不错的即时激励，可是却走向了错误的方向，导致长期的累积激励不高。
为了衡量在某个状态时的长期累积激励，我们定义状态值函数$V_{\pi }(s)$为在策略概率分布和转移概率分布下的长期回报:
$$\begin{array}{rl}{V}_{\pi }(s)& ={\mathbb{E}}_{\pi }[G_t|S_t=s]\\ & ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}...|S_t=s]\end{array}$$
发现$V_{\pi }(s)$具有递归关系：
$$\begin{array}{rl}{V}_{\pi }(s)& ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3}...)|S_t=s]\\ & ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma V_{\pi }(S_{t+1})|S_t=s]\\ & ={\mathbb{E}}_{\pi }[R_{t+1}|S_t=s]+E_{\pi }[\gamma V_{\pi }(S_{t+1})|S_t=s]\\ & =\sum _{a\in A}\pi (a|s)R(s,a)+\sum _{a\in A}\pi (a|s)\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V_{\pi }(s^{\prime })\\ & =\sum _{a\in A}\pi (a|s)(R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V_{\pi }(s^{\prime }))\\ & =R^{\pi }+\gamma P^{\pi }{V}_{\pi }(S_{t+1})\end{array}$$
可见，$s$状态下的回报，可以从转移到的下一个状态的$S_{t+1}$计算/更新而来。这点对于后面的迭代求最优解很重要。

2.2 动作值函数（action value function / Q-value）

和状态值函数类似，我们还可以定义动作值函数：衡量某一状态下采取某个动作的长期累积回报：
$$\begin{array}{rl}{q}_{\pi }(s,a)& ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}...|S_t=s,A_t=a]\\ & ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma q_{\pi }(S_{t+1})|S_t=s,A_t=a]\\ & =R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V_{\pi }(s^{\prime })\end{array}$$
以上状态值函数和动作值函数都具有递归性质，两者都统称为贝尔曼方程（Bellman equation）.可以看到，状态值函数和动作值函数的关系为：
$$V_{\pi }(s)=\sum _{a\in A}\pi (a|s)q_{\pi }(s,a)$$

2.3 最优的值函数（optimal value function）

强化学习是为了达到某种目标，比如机器人找到迷宫出口。“目标”我们可以用激励来量化体现，比如当机器人在迷宫出口位置时激励远远大于在其它位置上的。而出口位置往往不是一蹴而就的，而是要经过一段时间的“动作-状态转移”过程才能到达的。于是，我们的问题就变成最优（大）化累积激励，也就是最优化值函数：包括状态值函数和动作值函数。
最优状态值函数$V_{\star }(s)$:
$$V_{\star }(s)=\underset{\pi }{\max }{V}_{\pi }(s)$$
最优动作值函数$q_{\star }(s)$:
$$q_{\star }(s,a)=\underset{\pi }{\max }{q}_{\pi }(s,a)$$
得到最优值函数也就意味了找到了最优策略（optimal policy）${\pi }_{\star }$:
$${\pi }_{\star }=\underset{\pi }{\mathrm{argmax}}{V}_{\pi }(s)=\underset{\pi }{\mathrm{argmax}}{q}_{\pi }(s,a)$$
那么如何找到最优值函数呢？

2.4 MDP类型

求最优解之前，先明确一下MDP的两种形式：

• model-based
  即关于环境的所有信息都是已知的，即对于智能体来说，MDP的模型$⟨S,A,P,R,\gamma ⟩$是已知的，智能体要做的事情叫做规划（planning）.

• model-free
  即MDP的模型是不完全清楚的，比如状态转移概率未知等。这时智能体要做的就是学习（learning），强化学习的算法也主要是这一块。

不管是planning还是learning，都有两种问题：

1. 预测（prediction）
   给智能体一个的策略$\pi$. 计算出值函数$V_{\pi }$.
2. 控制（control)
   控制的意思其实就是优化。这时智能体没有明确的策略，而是要在所有策略分布中找出最优的值函数$V_{\star }$和最优策略${\pi }_{\star }$.

根据MDP是model-based或model-free、问题是planning还是learning，强化学习算法有如下分类：

	model-based	model-free
prediction	policy evalution	Monte-Carlo; TD
control	policy iteration; value iteration	Q-learning Sarsa

3. 策略迭代（policy iteration）和值迭代（value iteration）

这一部分是关于求解model-based的MDP问题的策略迭代和值迭代算法。策略迭代和值迭代都是为了求MDP的最优策略：每一状态对应的最优动作，两者是等价的。只不过策略迭代算完就完了，最优策略也就有了；而值迭代算完之后还需要进行一步最优策略的提取，当然这很简单，就是根据状态值函数求动作值函数而已。
在说求最优策略之前，先说怎么评估一个策略的优劣。一个策略越好，状态值函数越大。

3.1 策略评估（policy evaluation）

给定一个策略$\pi$，求状态值函数，根据状态函数的贝尔曼方程，我们有：
$$\begin{array}{rl}{V}_{\pi }(s)& ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma q_{\pi }(S_{t+1})|S_t=s,A_t=a]\\ & =\sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma V_{\pi }(s^{\prime })]\end{array}$$
这里$p$是转移概率函数，需要注意的是这里激励$r$和下一个状态$s^{\prime }$联系在一起，所以条件概率函数放在了中括号$[]$外面。
我们有$|S|$个状态，因此可以写出含有$|S|$个未知数的线性方程组，然后直接解方程组得到所有$V_{\pi }(s)$. 这不失为一种简单的方法，但是计算消耗较大。另一种方法就是迭代法，即初始时随便给$V_0(s)$一个值，然后在每个迭代步$k$, 根据贝尔曼方程迭代:
$$\begin{array}{r}{V}_{k+1}(s)\leftarrow \sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma V_k(s^{\prime })]\end{array}$$
第$k+1$步状态$s$，由上一步$k$的、$s$的下一个状态$s^{\prime }$计算得来。可以证明，当$k\to \infty$时$V_{k+1}(s)$趋于$V_{\pi }(s)$. 循环迭代的终止条件是$V_{k+1}(s)$ 和$V_k(s)$的差别小于某个设定的误差阈值。

3.2 策略改善（policy improvement）

既然我们能够评估一个策略，计算出策略对应的状态值函数，那么一个直接的想法就是怎么对策略进行改善。把原有策略$\pi$改善成${\pi }^{\prime }$的方法是找到令状态值函数最大的那个动作：
$$\begin{array}{rl}{\pi }^{\prime }& =\underset{a}{\mathrm{argmax}}{V}_{\pi }(s,a)\\ & =\underset{a}{\mathrm{argmax}}\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma V_k(s^{\prime })]\end{array}$$

3.3 策略迭代

有了上面的策略评估和策略改善，就可以很自然地进行策略迭代：先随便给个策略，计算状态值函数（策略评估）；然后根据状态值函数更新/改善策略（策略改善）；再由改善了的策略进行新的策略评估；接着又是策略改善…如此循环，直到这一步更新得到的策略已经和上一步的一样为止。

3.4 值迭代

策略迭代是不断地进行 “评估（值函数计算）- 改善（更新策略）”，而值迭代则是只进行值函数更新，直到值函数已经是最大化的时候，才一次性地提取出最优策略出来。值函数的更新还是贝尔曼方程，只不过这里不是取期望的状态值函数，而是取最大值的：
$$\begin{array}{r}{V}_{k+1}(s)\leftarrow \underset{a}{\max }\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma V_k(s^{\prime })]\end{array}$$

3.5 一个例子

(代码)

4. model-free prediction: MC & TD

4.1 MC

在model-based的MDP问题里，由一个策略计算状态值函数可以通过贝尔曼方程：
$$\begin{array}{rl}{V}_{\pi }(s)& ={\mathbb{E}}_{\pi }[G_t|S_t=s]\\ & =\sum _{a\in A}\pi (a|s)(R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V_{\pi }(s^{\prime }))\end{array}$$
但在model-free的MDP里转移概率是未知的。我们可以先进行一系列实验通过统计来估计一个转移概率分布，这有点像机器学习。但这里我们通过另一种方法：蒙特卡洛（MC）来直接近似地求值函数。
MC想法很简单，就是不断地重复实验（episodes），只要在实验中状态$s$被访问到了，就记录该次实验$s$的回报，最后用所有回报的平均值当作状态$s$的状态值。也就是说，我们不再计算状态$s$的期望回报（因为不知道概率分布），而是计算所有实验样本的平均回报：
$$\begin{array}{rl}& V_{\pi }(s)=\underset{N(s)\to \infty }{\lim }\frac{S(s)}{N(s)}\\ \text{where }& \text{episode number }N(s)\leftarrow N(s)+1\\ & \text{total return }S(s)\leftarrow S(s)+1\end{array}$$
上面这种计算方法是得到了所有回报之后再求平均值，事实上还有一种动态的方法。考虑计算$\{x_j\}$的平均值${\mu }_k$:
$$\begin{array}{rl}{\mu }_k& =\frac{1}{k}\sum _{j=1}^k{x}_j\\ & =\frac{1}{k}(x_k+\sum _{j=1}^{k-1}{x}_j)\\ & =\frac{1}{k}(x_k+(k-1){\mu }_{k-1})\\ & ={\mu }_{k-1}+\frac{1}{k}(x_k-{\mu }_{k-1})\end{array}$$
若状态$S_t$的回报是$G_t$，则$V(S_t)$可以通过下式的更新逼近平均值：
$$\begin{array}{rl}N(S_t)& \leftarrow N(S_t)+1\\ V(S_t)& \leftarrow V(S_t)+\frac{1}{N(S_t)}(G_t-V(S_t))\end{array}$$
利用这种方法迭代，每一次实验更新一次，就可以把更早之前的那些状态值都抛弃掉了。
这里我们可以把$\frac{1}{N(S_t)}$用$\alpha$替代:
$$\begin{array}{rl}V(S_t)& \leftarrow V(S_t)+\alpha (G_t-V(S_t))\end{array}$$
$\alpha$表示值更新的步长。迭代开始前可以给$V(S_t)$一个随机值，每一步迭代，就是把$G_t$看作目标值（target）,目标值和实际值的误差是$(G_t-V(S_t))$，那么我们就是以这个误差来更新实际值。这种方法叫增量迭代方法（incremental method）

4.2 Temporal-Difference （时间差分，TD）

在MC的方法中，我们更新一个状态值函数，是要等到一次实验完全完成了之后、有了回报$G_t$才能计算。与此相对应的TD算法，则是不需要等到实验全部完成，而是从$V(S_t)$走一步到$V(S_{t+1})$、得到一个激励$R_{t+1}$，就马上进行更新：
$$\begin{array}{rl}V(S_t)& \leftarrow V(S_t)+\alpha (R_{t+1}+\gamma V(S_{t+1})-V(S_t))\end{array}$$
这里$R_{t+1}+\gamma V(S_{t+1})$叫估计回报（estimated return）。注意这里$V(S_{t+1})$是上一次实验更新得到的、下一个状态的值函数，所以$R_{t+1}+\gamma V(S_{t+1})̸=G_t$.
这里可以另外定义一个量，叫TD-error ${\delta }_t=R_{t+1}+\gamma V(S_{t+1})-V(S_t)$.
这种不等到整个实验结束就利用下一步的值来更新当前步的值方法，叫bootstrapping方法。DP和TD都是bootstrapping方法。

	Sampling?	Bootstrapping?
DP	No	Yes
MC	Yes	No
TD	Yes	Yes

4.3 n-step TD, TD($\lambda$)

上面TD的值更新方法，是从$V(S_t)$往后看一步，到$V(S_{t+1})$. 那么是不是可以往后多看几步，用后面几步的估计回报来更新$V(S_t)$呢？假设我们多往后看$n$步，第$n$步的回报叫$G_t^{(n)}$:
$$G_t^{(n)}=R_{t+1}+\gamma R_{t+2}+...+{\gamma }^{n}V(S_{t+n})$$
n-step TD更新方法：
$$\begin{array}{rl}V(S_t)& \leftarrow V(S_t)+\alpha (G_t^{(n)}-V(S_t))\end{array}$$
当$n=1$时，$G_t^{(n)}$就是上面讲过的TD的估计回报$R_{t+1}+\gamma V(S_{t+1})$；当$n=\infty$时，则$G_t^{(n)}=G_t$，TD和MC就是一样的了！
那么$n$应该取几？是往后看5步好还是10步好？其实我们可以把所有的$G_t^{(n)}$利用权重加和起来，这样就可以利用每一步的信息了。把综合了所有步数的回报叫$\lambda$-return $G_t^{\lambda }$ （$\lambda \in [0,1]$）:
$$\begin{array}{rl}{G}_t^{\lambda }& =(1-\lambda )G_t^{(1)}+(1-\lambda )\lambda G_t^{(2)}+...+(1-\lambda ){\lambda }^{n-1}{G}_t^{(n)}\\ & =(1-\lambda )\sum _{n=1}^{\infty }{\lambda }^{n-1}{G}_t^{(n)}\end{array}$$
$(1-\lambda ){\lambda }^{n-1}$是权重。为什么选择这样的权重呢？首先这种权重满足和为1的条件，其次是因为这样的直觉：离当前越远的状态，对现在的影响越小，所以$\lambda$的幂次数越大。
此时TD更新方法就是：
$$\begin{array}{rl}V(S_t)& \leftarrow V(S_t)+\alpha (G_t^{\lambda }-V(S_t))\\ \text{or }V(S_t)& \leftarrow V(S_t)+\alpha ((1-\lambda )\sum _{n=1}^{\infty }{\lambda }^{n-1}{G}_t^{(n)}-V(S_t))\end{array}$$
这就叫TD($\lambda$)。这里我们要综合考虑未来的n步，来更新当下的状态，这样的方式叫做Forward-View TD($\lambda$). 往未来看n步、等到n步都走完了再更新当前状态值。但这有问题，就是每次更新状态值，要等到n步都走完了才能进行，这就缺乏了TD那种走一步、更新一步的online性质了。
为此，我们使用另一种更新状态的方式，叫Backward-View TD($\lambda$), 想法与Forward-View相反：不再往未来看，而是每走一步，忘过去看；每走一步就更新过去的n步。计算方法是：
$$\begin{array}{rl}& V(s)\leftarrow V(s)+\alpha {\delta }_t{E}_t(s)\\ \text{where }& {\delta }_t=R_{t+1}+\gamma V(S_{t+1})-V(S_t)\\ & E_t(s)=\gamma \lambda E_{t-1}(s)+1(S_t=s)\text{ with }{E}_0(s)=0\end{array}$$
$E_t(s)$叫做Eligibility Trace.

4.4 MC和TD的比较

回过头看，model-free的n-step TD($\lambda$)增量式值函数更新方法：
$$\begin{array}{rl}V(S_t)& \leftarrow V(S_t)+\alpha ((1-\lambda )\sum _{n=1}^{\infty }{\lambda }^{n-1}{G}_t^{(n)}-V(S_t))\end{array}$$
统一了MC和TD, 或者说这两者是n-step TD($\lambda =0$)的两种极端情况：

• $n=1\to$ TD
• $n=\infty \to$ MC

虽说被统一了，但还是有必要看看这两种极端情况的区别，当选择$n$的时候也知道会影响到什么。

MC要让一个episode完全进行完了再更新所有值函数，值函数是朝着实际目标$G_t$的方向去更新的；TD则不需要一个完整的episode，每走一步就更新一次，值函数更新方向是估计回报$R_{t+1}+\gamma V(S_{t+1})$.
$G_t$是从值函数最原始定义：回报的数学期望而来的（虽然用采样平均值代替期望），所以它是对真实的值函数$V_{\pi }(s)$的无偏估计（unbiased estimate）. 而显然，$R_{t+1}+\gamma V(S_{t+1})$和$G_t$还相差了很多项，所以$R_{t+1}+\gamma V(S_{t+1})$是对$V_{\pi }(s)$的有偏估计（biased estimate）.
而另一方面，MC方法中随机采集了几乎所有状态和动作样本，导致$G_t$的方差较大；相反，$R_{t+1}+\gamma V(S_{t+1})$方差较小。

在收敛性质上，MC是朝着最小化样本方差的方向收敛，也就是MC的结果更能吻合episodes的数据样本，倾向于类似监督学习里的“过拟合”，而和MDP这种模型的马尔科夫性关联性较小。相反，TD的收敛方向是最大化马尔科夫似然性，更加符合MDP模型。

	偏差	方差	收敛
MC	0	大	最小化方差
TD	大	小	最大化马尔科夫似然性

5 model-free control

因为是control / learning 问题，也就是找出最优策略问题，我们回到第3部分的策略迭代方法；因为这是model-free，我们要用到第4部分的MC或TD.
因为TD相对于MC有方差小、在线更新值函数、吻合马尔科夫性的优点，我们这里选择TD作为策略评估和策略改进的基本方法。

Model-free control有两种基本的类型：

• 同策略（on-policy）学习: 就是从已知的$\pi$中，通过采样实验的方法来学习策略$\pi$，代表方法是以TD为基础的Sarsa算法
• 异策略（off-policy）学习: 就是看着别人的策略$\mu$， 通过采样实验的方法来学习策略$\pi$，代表方法是以TD为基础的Q-learning算法

5.1 Q值函数

值函数有两种：状态值函数$V(s)$和动作值函数$Q(s,a)$，也叫Q值函数. 在第3部分model-based中，我们用$V(s)$来进行策略评估和策略改进，可是在model-free时却不能再用它，因为我们不知道MDP的状态转移函数$p$，而基于$V(s)$的策略改进却需要：
$$\begin{array}{rl}{\pi }^{\prime }& =\underset{a}{\mathrm{argmax}}\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma V_k(s^{\prime })]\end{array}$$
替代地，我们使用$Q(s,a)$：
$$\begin{array}{rl}{\pi }^{\prime }& =\underset{a}{\mathrm{argmax}}Q(s,a)\end{array}\text{\hspace{1em}(5-1)}$$
Q值函数的具体用法要看是采用同策略的Sarsa还是异策略的Q-learning算法。

5.2 $ϵ$-greedy

在式子（5-1）策略改进中，我们每一步都是选择让Q值最优的策略，但这是不是一定是最终最优的策略呢？比如有两扇门A和B，第一次打开A，什么都没有；第二-五次都是打开B，都得到了10块钱。很显然到目前为止，根据最大化Q值的方法，接下来还要打开B。可是打开A真的会一直都没收获吗？有没有可能某次打开A换来1000块呢？要不要试一下？

理性告诉我们，大多数时候还是应该选择B的，但是可以以一定的几率$ϵ$去打开A试一下。已经比较确定打开B会有一定收益，这叫exploitation；而试一试打开A，碰碰运气，这叫$ϵ$-greedy exploration. 假设有$m$次实验，那么我们的$ϵ$-greedy策略就应该是：
$$\pi (a|s)=\{\begin{array}{ll}ϵ/m+1-ϵ,& \text{if }a=argmaxQ(s,a)\\ ϵ/m,& \text{otherwise}\end{array}$$
事实上任何$ϵ$-greedy策略${\pi }^{\prime }$都是对原有策略$\pi$的改进，证明如下：
$$\begin{array}{rl}{V}_{{\pi }^{\prime }}(s)& =\sum _a{\pi }^{\prime }(a|s)q_{\pi }(a,s)\\ & =\underset{\text{exploitation}}{ϵ/m\sum _a{q}_{\pi }(a,s)}+\underset{\text{exploration}}{(1-ϵ)\underset{a}{\max }{q}_{\pi }(a,s)}\\ & \ge ϵ/m\sum _a{q}_{\pi }(a,s)+\underset{\text{because max >= any weighted sum}}{(1-ϵ)\sum _a\frac{\pi (a|s)-ϵ/m}{1-ϵ}{q}_{\pi }(a,s)}\\ & =\sum _a\pi (a|s)q_{\pi }(a,s)\\ & =V_{\pi }(s)\end{array}$$
一般来说，在循环迭代的最初，我们设置$ϵ=1$，意思是最开始的时候我们对于环境一无所知，唯一能做的就是exploration. 而随着迭代次数的增加，$ϵ$ 逐渐减小。每次迭代都是产生一个0和1之间的随机数，如果随机数比$ϵ$ 大则采取exploitation, 反之则exploration. 当迭代至尾声时，$ϵ$ 应该接近0, 即此时我们对环境已有相当的了解，要做的就只是exploitation.

5.3 Sarsa

Sarsa = S - A - R - S’ - A’，模型如下图：

就是说从一个状态-动作对（S, A）出发，得到一个激励R，到达下一个状态S’, 然后根据策略再采取动作A‘, 如此循环下去。Sarsa 是一种on-policy的策略迭代方法，原理和model-based里的策略迭代一样，即策略评估和策略改进交替进行，直到收敛：

• 策略评估：其实就是TD了，只不过这里把TD里的状态值函数换成动作Q值函数，如（5.1）所说的。
  $$\begin{array}{rl}Q(S,A)& \leftarrow Q(S,A)+\alpha (R+\gamma Q(S^{\prime },A^{\prime })-Q(S,A))\end{array}\text{\hspace{1em}(5-3)}$$
• 策略改进：$ϵ$-greedy策略改进

在TD里我们还用到了n-step和$\lambda$参数，这里也是一样的道理，策略评估可以进一步拓展成Forward-View的形式：
$$\begin{array}{rl}Q(S_t,A_t)& \leftarrow Q(S_t,A_t)+\alpha (q_t^{\lambda }-Q(S_t,A_t))\\ \text{where }{q}_t^{\lambda }& =(1-\lambda )\sum _{n=1}^{\infty }{\lambda }^{n-1}{q}_t^{(n)}\end{array}$$
为了能online计算，和TD($\lambda$)一样，我们用Eligibility Trace把上式改成Backward-View的形式：
$$\begin{array}{rl}& Q(s,a)\leftarrow Q(s,a)+\alpha {\delta }_t{E}_t(s,a)\\ \text{where }& {\delta }_t=R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S,A)\\ & E_t(s,a)=\gamma \lambda E_{t-1}(s,a)+1(S_t=s,A_t=a)\text{ with }{E}_0(s,a)=0\end{array}$$

5.4 Q-learning

Sarsa 更新Q值函数（式子（5-3）），是通过随机选择下一个$Q(S^{\prime },A^{\prime })$, 通过多次重复的实验我们其实是用下一个Q值的平均值来计算。与Sarsa不同的是，Q-learning采用了取最大值的方式更新Q值：
$$\begin{array}{rl}Q(S,A)& \leftarrow Q(S,A)+\alpha (R+\gamma \underset{a^{\prime }}{\max }Q(S^{\prime },a^{\prime })-Q(S,A))\end{array}$$
我们看下面这个表：
Sarsa 和 Q-learning本质都是TD，都是online地更新Q值函数，以逼近采样的平均值（这也是TD不同于DP的地方）。只不过，Sarsa是只看一个A’，而Q-learning是看Q值最大的那个A’.

6 值函数近似（value function approximation）

从model-based的DP, 到model-free的MC, TD, Sarsa, Q-learning等算法，我们更新状态值函数或者动作值函数时，都是准确地用到上一轮迭代产生的值函数。上一轮的值函数，存储在某个查找表格中，当这一轮迭代要用到时，就去表格中查找；这一轮计算完了之后，也就把表格更新了。像这样的能够把所有值函数存储在查找表格中、并准确地利用每一个值函数的方法，可以归结为Tabular Solution Method.
但现实问题中，状态或者状态-动作对的数量可能是极其大的，比如围棋中的状态数可以达到$10^{170}$. 这么大规模的数据，用表格的方法准确计算、记录每个值函数是不可行的。
因此，我们需要用一种近似的方法来估算值函数，即：
$$\begin{array}{rl}& \hat{v}(s,\omega )\simeq v_{\pi }(s)\\ \text{or }& \hat{q}(s,a,\omega )\simeq q_{\pi }(s,a)\end{array}$$
其中 $\omega$ 是参数，是我们要去找的、使得 $\hat{v}$ 和 $\hat{q}$ 尽可能接近准确值的参数。

6.1 梯度下降（Gradient Descent）

假设$J(\omega )$关于$\omega$是可微的，则$J(\omega )$的梯度可以写成：
$$\begin{array}{r}{\nabla }_{\omega }J(\omega )=\left(\begin{array}{c}\frac{\partial J(\omega )}{\partial {\omega }_1}\\ .\\ .\\ .\\ \frac{\partial J(\omega )}{\partial {\omega }_n}\end{array}\right)\end{array}$$
为了找到$J(\omega )$的最小值，$\omega$的迭代更新算法应该是：
$$\begin{array}{rl}& \omega \leftarrow \omega +\Delta \omega \\ \text{with }& \Delta \omega =-\frac{1}{2}\alpha {\nabla }_{\omega }J(\omega )\end{array}$$
$\alpha$叫做步长，是迭代更新的参数。
回到值函数近似。如果我们要找到$\hat{v}(s,\omega )\simeq v_{\pi }(s)$，也就是要两者的差最小，那么我们将问题转化为使如下的$J(\omega )$（叫目标函数）最小：
$$J(\omega )={\mathbb{E}}_{\pi }[(v_{\pi }(s)-\hat{v}(s,\omega ){)}^2]$$
则：
$$\begin{array}{rl}\Delta \omega & =-\frac{1}{2}\alpha {\nabla }_{\omega }J(\omega )\\ & =\alpha {\mathbb{E}}_{\pi }[(v_{\pi }(s)-\hat{v}(s,\omega )){\nabla }_{\omega }\hat{v}(s,\omega )]\end{array}$$
不知道概率分布没法求期望，我们转而用随机梯度下降（Stochastic gradient descent）的方法，即：
$$\begin{array}{rl}\Delta \omega & =\alpha (v_{\pi }(s)-\hat{v}(s,\omega )){\nabla }_{\omega }\hat{v}(s,\omega )\end{array}$$

6.2 线性函数近似

现在考虑怎么表示$\hat{v}(s,\omega )$. 一开始我们对值函数是一无所知的，但我们可以假设对于一个状态$s$来说，它应该是由很多个特征（feature）共同影响的。比如智能体在某个状态时，它的速度、朝向、到某处的距离可能决定了它在这个状态的值函数。为了表征这些特征，我们可以用线性组合来表示$\hat{v}(s,\omega )$：
$$\begin{array}{r}\hat{v}(s,\omega )=X(s{)}^{T}W=\sum _{j=1}^n{x}_j(s)w_j\end{array}$$
其中$X(s)$是包含n个分量的特征列向量，$x_j(s)$ 即是第j个分量，$w_j$是对应这个分量的参数，或者说权重。这时目标函数是：
$$J(\omega )={\mathbb{E}}_{\pi }[(v_{\pi }(s)-X(s{)}^{T}W{)}^2]$$
参数更新方法：
$$\begin{array}{rl}\Delta \omega & =\alpha (v_{\pi }(s)-\hat{v}(s,\omega ))X(s)\end{array}\text{\hspace{1em}(6-2)}$$

6.3 incremental method

式子(6-2)中用了$v_{\pi }(s)$，这是真实的值函数，可是这里不是监督学习，没有标记，没人告诉我们真实值函数是什么。因此，我们需要用到MC和TD中的目标值代替 $v_{\pi }(s)$：
$$\begin{array}{rl}\text{MC: }& \Delta \omega =\alpha (G_t-\hat{v}(S_t,\omega ))X(S_t)\\ \text{TD: }& \Delta \omega =\alpha (R_{t+1}+\gamma \hat{v}(S_{t+1},\omega )-\hat{v}(S_t,\omega ))X(S_t)\\ \text{TD}(\lambda )\text{: }& \Delta \omega =\alpha (G_t^{\lambda }-\hat{v}(S_t,\omega ))X(S_t)\end{array}$$
上面这个是对于状态值函数的，用于prediction. 如果是control问题，对于动作值函数，我们可以写出相似的形式：
$$\begin{array}{rl}\text{MC: }& \Delta \omega =\alpha (G_t-\hat{q}(S_t,A_t,\omega ))X(S_t,A_t)\\ \text{TD: }& \Delta \omega =\alpha (R_{t+1}+\gamma \hat{q}(S_{t+1},A_{t+1},\omega )-\hat{v}(S_t,\omega ))X(S_t,A_t)\\ \text{TD}(\lambda )\text{: }& \Delta \omega =\alpha (G_t^{\lambda }-\hat{q}(S_t,A_t,\omega ))X(S_t,A_t)\end{array}$$
以上这种更新$\omega$的方法叫 incremental method，意思是每走一步就更新一次。

6.4 batch method

incremental method 更新很快，可是却有一个问题：每走一步更新一次，也就意味着每走一步丢弃一次数据，不能充分利用既有的学习经验。因此提出了与 incremental method 对应的 batch method.
考虑一个针对策略$\pi$ 的 prediction问题。智能体已经有了不少经验，所谓经验就是一系列的$⟨state,value⟩$对。把经验定义成数据集$\mathbf{D}$:
$$\mathbf{D}=\{⟨s_1,v_1^{\pi }⟩,⟨s_2,v_2^{\pi }⟩...⟨s_n,v_n^{\pi }⟩\}$$
如何确定参数$\omega$，使得$\hat{v}(s,\omega )$尽可能地 fit 数据集$\mathbf{D}$？方法是 Least Squares (LS) 算法，思路很直接，就是最小化下面这个式子：
$$\begin{array}{rl}LS(\omega )& =\sum _{t=1}^n(v_t^{\pi }-\hat{v}(S_t,\omega ){)}^2\\ & ={\mathbb{E}}_{\mathbf{D}}[(v^{\pi }-\hat{v}(S,\omega ){)}^2]\end{array}$$
结合梯度下降的具体算法是：

1. 抽样 $⟨s,v^{\pi }⟩\sim \mathbf{D}$
2. 迭代 $\Delta \omega =\alpha (v(s)-\hat{v}(s,\omega )){\nabla }_{\omega }\hat{v}(s,\omega )$

迭代至收敛，最后${\omega }^{\pi }=\underset{\omega }{\mathrm{argmin}}LS(\omega )$
另一种batch method 是 Deep Q-Network (DQN)， 思路和Q-learning 类似。这里我们把经验数据集拓展成：
$$\mathbf{D}=\{⟨s_t,a_t,r_{t+1},s_{t+1}⟩\}$$
LS公式变成：
$$\begin{array}{rl}LS(\omega )& ={\mathbb{E}}_{s,a,r,s^{\prime }\sim \mathbf{D}}[(r+\gamma Q(s^{\prime },a^{\prime };{\omega }^{-})-Q(s,a;\omega ){)}^2]\end{array}$$