《信号与系统》解读 第3章 强大的傅里叶时域频域分析工具-1:深入理解信号的时域与频域,需要从熟悉的声音信号入手
目录
1. 信号与系统的组成
1.1 什么是信号?
1.2 什么是系统?
2. 声音信号的时域表现
2.1 时域波形的定义
2.2 声音信号的时域波形
3. 声音信号的频率组成
3.1 单音:单一频率的声音
3.2 和声:多种频率声音的混合
3.3 音乐:不同单音或和声的有机组合
3.4 声音信号的频率范围
4. 波的叠加原理
4.1 同频波的时域放大叠加: 声音的叠加
4.2 同频波的时域抵消叠加: 声音的抵消
4.3 不同频率波的时域叠加
5. 频域分析
5.1 为什么需要频率分析?
5.2 信号的频率组成?
6. 时域与频域转换的数学工具
6.1 傅里叶分析的强大能力
6.2 案例演示
1. 信号与系统的组成
![]()
1.1 什么是信号?
- 广义信号:是运载消息的工具,是消息的载体。从广义上讲,根据用途分为光信号、电信号、温度、压力、流量,自然界的声音信号等。
- 狭义信号:是指随着时间而变化的电压或电流信号。电信号可以通过幅度、频率、相位的变化来表示不同的消息。
本文以我们熟悉的声音信号来阐述关于电信号的最基础、也是最核心的两个概念:信号的频率和频域。
因为声音信号与电信号都具有“波”的特性!
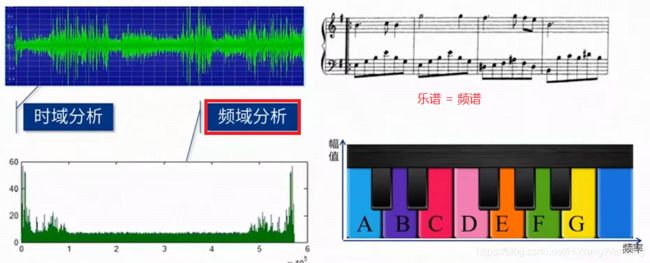
频域与时域其实是分析同一信号的两个不同的方面,并不是两种不同类型的信号。
时域波形:是信号外在的综合表现,时域波形是时间t为自变量,幅度或强度为因变量的可视化的图形展示。有时候也称为时域信号。
频域频谱:是信号内在的成分组成。频域频谱是组成的频率分量f为自变量,幅度或强度为因变量的可视化的图形展示。有时候也称为频率信号。
1.2 什么是系统?
- 广义系统:对信号进行运算、处理的实体称为系统。
- 狭义系统: 在《系统与系统》中,把能加工、变换电信号的实体称作“系统”。整个信号与系统就围绕着电信号的幅度、频率、相位来进行的!!
2. 声音信号的时域表现
2.1 时域波形的定义
是描述数学函数或物理信号对时间的关系。是信号外在的综合表现。
时域波形是时间t为自变量,幅度或强度为因变量的可视化的图形展示。表达信号幅度随着时间的变化的规律。
若考虑离散时间,时域中的函数或信号,在各个离散时间点的数值均为已知。
若考虑连续时间,则函数或信号在任意时间的数值均为已知。
在研究时域的电信号时,常会用示波器来观察电信号时域的波形。
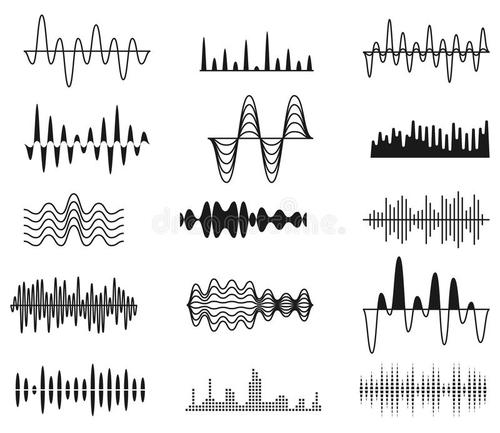
2.2 声音信号的时域波形
声音(sound)是由物体振动产生的声波。
是通过介质(空气或固体、液体)传播并能被人或动物听觉器官所感知的波动现象。
最初发出振动(震动)的物体叫声源。
这是声音信号时域波形,是声音信号外在的表现。
3. 声音信号的频率组成
声音以波的形式振动(震动)传播。
自然界的声音是多种不同频率基本的声音信号的混合而成。
每一种基本的声音信号就是特定频率的正弦波
正弦波是频率成分最为单一的一种信号,因这种信号的波形是数学上的正弦曲线而得名。
任何复杂信号——例如音乐信号,都可以看成由许许多多频率不同、大小不等的正弦波复合而成。
这个结论很重要,更进一步的理解这个概率,不妨看一下钢琴弹出的声音
3.1 单音:单一频率的声音
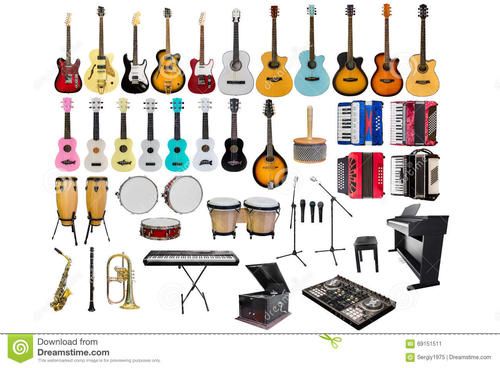
钢琴上不同键盘代表不同频率的声音:
不同乐器发出声音的频率是不一样的:
3.2 和声:多种频率声音的混合
3.3 音乐:不同单音或和声的有机组合
它的基本要素包括音的高低,音的长短,音的强弱和音色。
由这些基本要素相互结合,形成 音乐的常用的“形式要素”,例如:节奏,曲调,和声,以及力度,速度,调式,曲式,织体等。
构成音乐的形式要素,就是音乐的表现手段。不同类型音乐可能会强调或忽略其中的某些元素。
3.4 声音信号的频率范围
频率小于20Hz的信号称为亚音信号,或称为次音信号;
频率高于20KHz的信号称为超音频信号,或称超声波信号。
频率范围为20Hz-20kHz的信号人的听觉器官能感知的声音频率, 称为音频信号;
虽然人的发音器官发出的声音频率是80Hz-3400Hz,但人说话的信号频率通常为300-3000Hz,人们把在这种频率范围的信号称为话音信号;
4. 波的叠加原理
如果有两列以上的同类波在空间相遇,在共存的空间内,总的波是各个分波的矢量和(即相加时不仅考虑振幅,还考虑相位),而各个分波相互并不影响,分开后仍然保持各自的性质不变。
叠加后的外显的波形,就是时域波形。
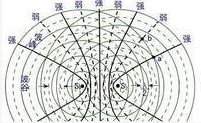
波的干涉:物理学现象。频率相同的两列波叠加,使某些区域的振动加强,某些区域的振动减弱,而且振动加强的区域和振动减弱的区域相互隔开。这种现象叫做波的干涉。波的干涉所形成的图样叫做干涉图样。
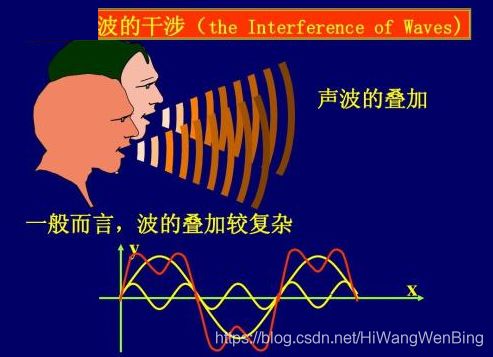
4.1 同频波的时域放大叠加: 声音的叠加
4.2 同频波的时域抵消叠加: 声音的抵消
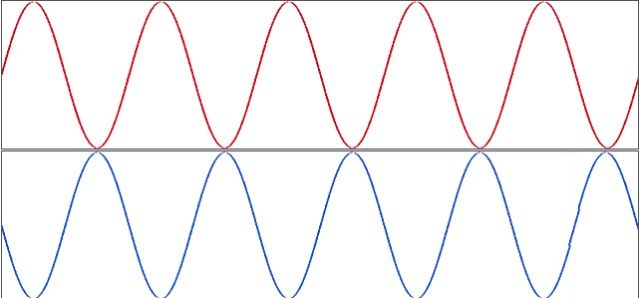
同频、同相位的波可以叠加在一起,这很容易理解。
4.3 不同频率波的时域叠加
不同频率的波的叠加比较复杂,如下图所示,叠加后的波形是就是时域波形。
5. 频域分析
5.1 为什么需要频率分析
(1)频率是信号的本质组成
时域信号的表现是信号的外在表现,而信号的频率分量组成才是信号内在的本质。通过频域分析,可以理解信号的本质。
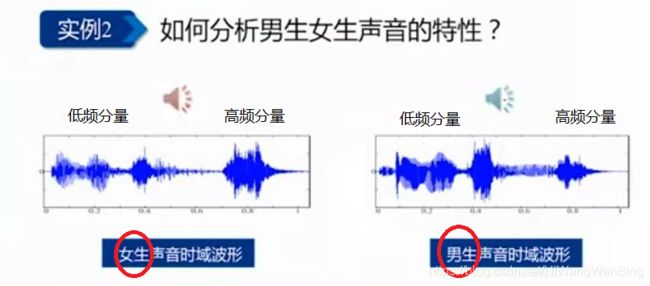
(2)通过频率分析信号的本质特性
如通过频域分析,可以看出:女性声音相对于男性,高频声音信号比男性多,且高频信号的幅度比男性高。
而男性的声音,低频分量比女性多。
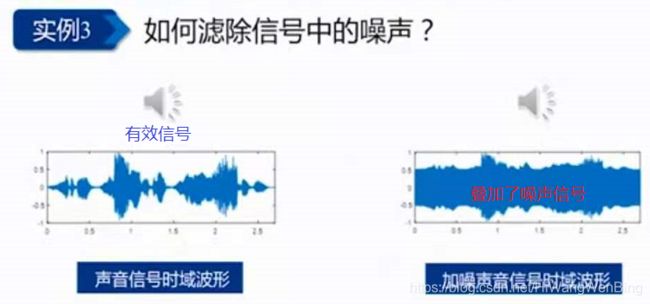
(3)通过频率分量,可以去除特定频率的噪声信号
很显然,直接时域信号,是无法去除噪声的。
当通过频率分析,可以发现,噪声的频率是确定的,就可以通过“滤波器“、”,直接滤除特定频率的噪声信号,留下原先的有用的声音信号。
去噪非常方便!!!
5.2 信号的频率组成:频谱?
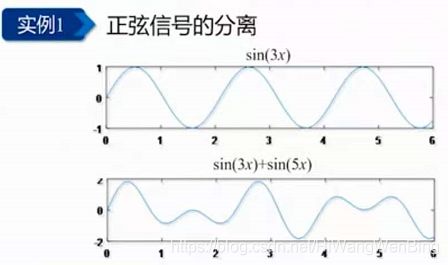
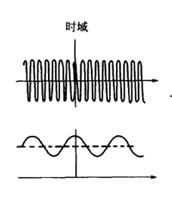
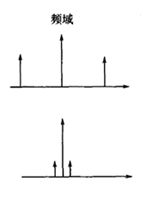
(1)时域信号的频率分解与频率分量的组成
![]()
结论:
- 不同频率的信号是可以混在一起的,
- 且只要方法得当,可以把原先不同频率的信号分离出来。
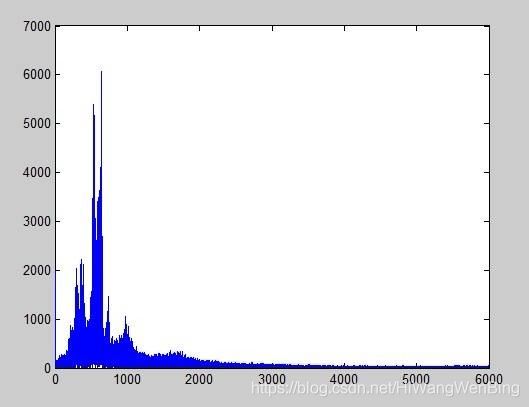
(2)不同频率分量的幅度:频域信号
频域frequency domain 是描述信号在频率方面特性时用到的一种坐标系。
频域特性:信号是由哪些单一频率的信号合成的,以及每个单一频率的比重/幅度。
- 单音(或称为单频率)信号的频域表示
- 含有2个频率分量的频域表示
- 含有多个连续的频率分量的频域表示
6. 时域与频域转换的数学工具
频谱分析:是一种将复杂信号分解为较简单信号的技术。许多物理信号均可以表示为许多不同频率简单信号的和。
找出一个信号在不同频率下的信息(如振幅、功率、强度或相位等)的做法即为频谱分析。
傅里叶分析方法:时域到频域的转换、时域到频率转换的强大数学工具!是信号与系统中几大基本分析工具之一。
傅里叶分析理论基础:任何信号,都可以表示为不同频率的复指数信号(正弦信号)的无限叠加!
包括:连续周期信号、离散周期信号、连续非周期信号、离散非周期信号。
6.1 傅里叶分析的强大能力
(1)强大的时域和频域分析能力
不同时域信号内部的频率组成是不一样的,通过统一的傅里叶变换数学工具,可以分析任何时域信号的内部频率组成。
(2)强大的信号合成与分解能力
可以把任何时域信号分解成频域的不同频率的信号,也可以把频域的不同的频率的信号合成为任意的时域信号。
![]()
(3)精确的量化能力
傅里叶不仅仅能否分析时域信号内含多少频率分量F(t),还能够分析不同频率分量的幅度A(t)和相位P(t)。
频率分量、幅度分量、相位分量,可能是离散的,也可能是连续的!完全精确量化!
请参看后续文章,深入探讨傅里叶分析方法的详细内容。
这里只给出2个定性分析的案例演示。
6.2 案例演示
示例1:
蓝色的线:是不同频率分量的信号的各自的频率以及他们各自的幅度。
红色的线:是不用频率分量的信号的混合后的信号。
![]()
示例2:方波信号
方波信号由不同的频率、不同幅度的正弦波组成。
![]()
矩形脉冲:持续持续时间越短,能量密度越大,主瓣上的频率分量越多。
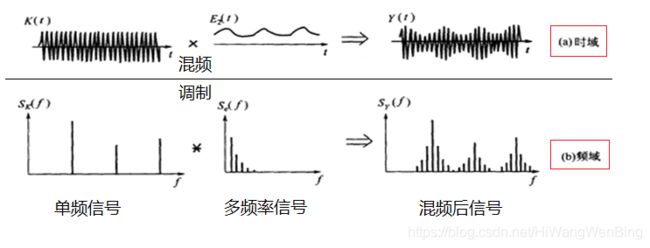
在模拟调制时,实际上是把每个频率分量都调制到高频载波上。但高频分量越高,对载波信号的频率要求就越高。
载波的频率越高,可以调制的基带信号的内含的频率分量就越多。