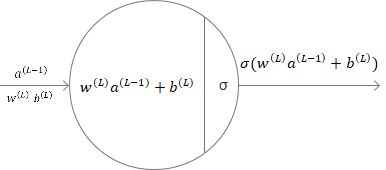神经网络学习笔记(3)——梯度下降公式讲解与反向传播算法
结合上上两篇文章的叙述,这一篇文章主要讲解梯度的公式的推导,笔记来自于3B1B的视频,链接会放在最后。
同样的,这一篇文章依旧没有代码。
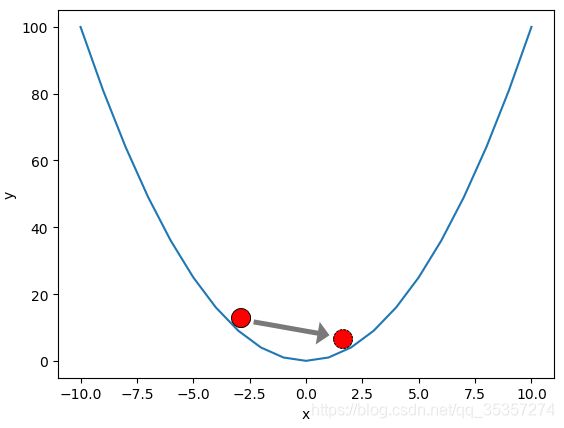
上篇文章中稍稍写漏了点东西,就是说在梯度下降过程中,步长是与该点的斜率有关,如果无关的话,那么如果步长太大,是不是就从坑中心滚过去了呀?比如这样:
下面开始正文。
每层只有一个神经元
根据上篇文章的内容,梯度会有正有负,代表的意思就是这个点该如何移动。而每一项的相对大小告诉了改变哪个值影响更大。如下图所示:

由于在神经网络中,我们的经验风险是在最后一步才求得的,那么我们只能从最后超最前一层一层地来调整权重和偏差,所以这个调整的算法就叫反向传播算法(Back Propagation,BP)。
我们假设这个是输出层的神经元,且上层只有一个输入,那么输出值: a ( L ) = σ ( z ( L ) ) a^{(L)} = \sigma(z^{(L)}) a(L)=σ(z(L)), z ( L ) = w ( L ) a ( L − 1 ) + b ( L ) z^{(L)} = w^{(L)}a^{(L-1)}+b^{(L)} z(L)=w(L)a(L−1)+b(L),此处 σ \sigma σ为激活函数(如sigmoid、tanh或者ReLU)。
这里为什么是 W ( L ) W^{(L)} W(L)和 b ( L ) b^{(L)} b(L),却是 a ( L − 1 ) a^{(L-1)} a(L−1),这是因为第一篇文章提到的,W和b是针对这一层,而输入值是上一层的输出。
而相应的,代价为 c o s t = ( a ( L ) − y ) 2 cost = (a^{(L)} - y)^2 cost=(a(L)−y)2,此处y是我们的期望值。
用3B1B构建的树状结构表达如下:

又上篇文章中提到的,要求最小值,那么就是求极值点,即偏导为0的地方,那么我们先对w求偏导,根据链式法则或者说上面树状图所得,公式如下:
∂ c o s t ∂ w ( L ) = ∂ z ( L ) ∂ w ( L ) ∂ a ( L ) ∂ z ( L ) ∂ c o s t ∂ a ( L ) \frac{\partial cost}{\partial w^{(L)}}=\frac{\partial z^{(L)}}{\partial w^{(L)}} \frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial cost}{\partial a^{(L)}} ∂w(L)∂cost=∂w(L)∂z(L)∂z(L)∂a(L)∂a(L)∂cost
上面式子中结果 ∂ c o s t ∂ w ( L ) \frac{\partial cost}{\partial w^{(L)}} ∂w(L)∂cost指的是w的改变对cost的影响,第一个偏导 ∂ z ( L ) ∂ w ( L ) \frac{\partial z^{(L)}}{\partial w^{(L)}} ∂w(L)∂z(L)指的是w的变化对z变化的影响,后面两个也是同理的。
那么也就是说,w的改变会影响到z,z的改变会影响到a,a的改变最终影响到cost。
这里我先罗列出上面的所有式子,避免大家还要翻上面慢慢找:
a ( L ) = σ ( z ( L ) ) a^{(L)} = \sigma(z^{(L)}) a(L)=σ(z(L))
z ( L ) = w ( L ) a ( L − 1 ) + b ( L ) z^{(L)} = w^{(L)}a^{(L-1)}+b^{(L)} z(L)=w(L)a(L−1)+b(L)
c o s t = ( a ( L ) − y ) 2 cost = (a^{(L)} - y)^2 cost=(a(L)−y)2
那么我们就逐一求偏导来找寻每一个式子的意义:
∂ c o s t ∂ a ( L ) = 2 ( a L − y ) \frac{\partial cost}{\partial a^{(L)}}=2(a^{L}-y) ∂a(L)∂cost=2(aL−y),这个偏导意味着导数的大小跟网络最终的输出( a ( L ) a^{(L)} a(L))减目标结果( y y y)的差成正比。而这里是二倍,那么就是说如果w改变了一点,那么至少在最后这里的差值会被放大两倍。
∂ a ( L ) ∂ z ( L ) = σ ′ ( z ( L ) ) \frac{\partial a^{(L)}}{\partial z^{(L)}}=\sigma'(z^{(L)}) ∂z(L)∂a(L)=σ′(z(L)),这里就是说的对选择的激活函数求导,求导意味着斜率或者说变化率,也就对应了本文最开始提到的梯度的正负值以及相应的步长。
∂ z ( L ) ∂ w ( L ) = a ( L − 1 ) \frac{\partial z^{(L)}}{\partial w^{(L)}}=a^{(L-1)} ∂w(L)∂z(L)=a(L−1),这个偏导指的意思是, w w w对 z z z的改变量取决于前一层的神经元,我们就可以看出,由这个式子,将上下两层的神经元进行的关联。
当然,这个是只有一个训练样本的情况,但是现实生活中训练样本是成千上万的,所以最终的结果要取算术平均值,公式如下:
∂ c o s t ∂ w ( L ) = 1 n ∑ k = 0 n − 1 ∂ c o s t k ∂ w ( L ) \frac{\partial cost}{\partial w^{(L)}}=\frac{1}{n}\sum_{k=0}^{n-1}\frac{\partial cost_k}{\partial w^{(L)}} ∂w(L)∂cost=n1k=0∑n−1∂w(L)∂costk
同理,对于b的偏导如下:
∂ c o s t ∂ b ( L ) = ∂ z ( L ) ∂ b ( L ) ∂ a ( L ) ∂ z ( L ) ∂ c o s t ∂ a ( L ) \frac{\partial cost}{\partial b^{(L)}}=\frac{\partial z^{(L)}}{\partial b^{(L)}} \frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial cost}{\partial a^{(L)}} ∂b(L)∂cost=∂b(L)∂z(L)∂z(L)∂a(L)∂a(L)∂cost
这里唯一有变化的就是 ∂ z ( L ) ∂ b ( L ) \frac{\partial z^{(L)}}{\partial b^{(L)}} ∂b(L)∂z(L),得到的结果为: ∂ z ( L ) ∂ b ( L ) = 1 \frac{\partial z^{(L)}}{\partial b^{(L)}}=1 ∂b(L)∂z(L)=1,那么说明b的改变是不会影响到z的,最终的结果如下:
∂ c o s t ∂ b ( L ) = ∂ z ( L ) ∂ b ( L ) ∂ a ( L ) ∂ z ( L ) ∂ c o s t ∂ a ( L ) = σ ′ ( z ( L ) ) 2 ( a L − y ) \frac{\partial cost}{\partial b^{(L)}}=\frac{\partial z^{(L)}}{\partial b^{(L)}} \frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial cost}{\partial a^{(L)}}=\sigma'(z^{(L)})2(a^{L}-y) ∂b(L)∂cost=∂b(L)∂z(L)∂z(L)∂a(L)∂a(L)∂cost=σ′(z(L))2(aL−y)
得到的所有训练数据中的算术平均值如下:
∂ c o s t ∂ b ( L ) = 1 n ∑ k = 0 n − 1 ∂ c o s t k ∂ b ( L ) \frac{\partial cost}{\partial b^{(L)}}=\frac{1}{n}\sum_{k=0}^{n-1}\frac{\partial cost_k}{\partial b^{(L)}} ∂b(L)∂cost=n1k=0∑n−1∂b(L)∂costk
最终,将每一层的权重和偏置值放在一个矩阵中构成梯度(这里仍然是假定每一层只有一个神经元),如下:
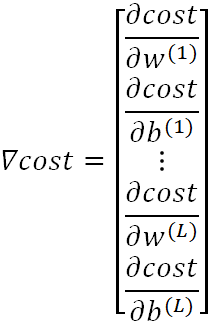
再补充一个,代价对上一层的激活值的敏感度,那么上面的公式我们就要改为对 a ( L − 1 ) a^{(L-1)} a(L−1)求偏导,那么整体结果如下:
∂ c o s t ∂ a ( L − 1 ) = ∂ z ( L ) ∂ a ( L − 1 ) ∂ a ( L ) ∂ z ( L ) ∂ c o s t ∂ a ( L ) = w ( L ) σ ′ ( z ( L ) ) 2 ( a L − y ) \frac{\partial cost}{\partial a^{(L-1)}}=\frac{\partial z^{(L)}}{\partial a^{(L-1)}} \frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial cost}{\partial a^{(L)}}=w^{(L)}\sigma'(z^{(L)})2(a^{L}-y) ∂a(L−1)∂cost=∂a(L−1)∂z(L)∂z(L)∂a(L)∂a(L)∂cost=w(L)σ′(z(L))2(aL−y)
虽然我们没法改变激活值,但是我们可以了解到,代价对上一层激活值的敏感度与权重有关。
每层有多个神经元
当有了上面的知识后,再来考虑实际中的情况,即每一层有多个神经元。
我们还是先从输出层开始看。
输出层无非就是从一个神经元输出扩展到了多个,相应的代价也就成了求和,公式如下:
C 0 = ∑ j = 0 n L − 1 ( a j ( L ) − y j ) 2 C_0=\sum_{j=0}^{n_L-1}(a_j^{(L)}-y_j)^2 C0=j=0∑nL−1(aj(L)−yj)2
这里的求和上标指的是第L层的神经元个数。
同理, a ( L ) a^{(L)} a(L)和 z L z^{{L}} zL也变为了如下:
a j ( L ) = σ ( z j ( L ) ) a_j^{(L)}=\sigma(z_j^{(L)}) aj(L)=σ(zj(L))
z j ( L ) = ∑ k = 0 n L − 1 − 1 ( w j k ( L ) a k ( L − 1 ) ) + b j ( L ) z_j^{(L)}=\sum_{k=0}^{n_{L-1}-1}(w_{jk}^{(L)}a_k^{(L-1)})+b_j^{(L)} zj(L)=k=0∑nL−1−1(wjk(L)ak(L−1))+bj(L)
这里需要注意的点在, w j k ( L ) w_{jk}^{(L)} wjk(L)的意思是,j是L层的神经元,k是L-1层的神经元,即从L-1层第k个神经元到L层第j个神经元,这样做的愿意是因为矩阵运算的缘故,详细的矩阵可以看我这个系列的第一篇文章。
偏导公式如下:
∂ c o s t ∂ w j k ( L ) = ∑ j = 0 n L − 1 ∂ z j ( L ) ∂ w j k ( L ) ∂ a j ( L ) ∂ z j ( L ) ∂ c o s t ∂ a j ( L ) \frac{\partial cost}{\partial w_{jk}^{(L)}}=\sum_{j=0}^{n_L-1} \frac{\partial z_j^{(L)}}{\partial w_{jk}^{(L)}} \frac{\partial a_j^{(L)}}{\partial z_j^{(L)}} \frac{\partial cost}{\partial a_j^{(L)}} ∂wjk(L)∂cost=j=0∑nL−1∂wjk(L)∂zj(L)∂zj(L)∂aj(L)∂aj(L)∂cost
至于每一个偏导的意义,我觉得这里只需要提 ∂ z j ( L ) ∂ w j k ( L ) \frac{\partial z_j^{(L)}}{\partial w_{jk}^{(L)}} ∂wjk(L)∂zj(L)。
∑ j = 0 n L − 1 ∂ z j ( L ) ∂ w j k ( L ) = ∑ j = 0 n L − 1 a k ( L − 1 ) = n L a k ( L − 1 ) \sum_{j=0}^{n_L-1} \frac{\partial z_j^{(L)}}{\partial w_{jk}^{(L)}}=\sum_{j=0}^{n_L-1}a_k^{(L-1)}=n_La_k^{(L-1)} j=0∑nL−1∂wjk(L)∂zj(L)=j=0∑nL−1ak(L−1)=nLak(L−1)
就是说L-1层的每个神经元都对这一层的这一个神经元起了作用。
注:这个偏导是自己推导的,因为 a k ( L − 1 ) a_k^{(L-1)} ak(L−1)不属于循环中的内容,当做常量考虑,那么求和就是 n L n_L nL个常量之和,所以推导出的最后这个公式。有可能有问题,如果有问题,欢迎指正。
写在最后
嗯,3B1B的理论部分讲完了,我这边要开始准备写代码了,算起来好像快一个月没写过代码了,全在看理论知识,争取国庆节完之前把BP的代码写好,并且讲解一遍。
参考
[1]3Blue1Brown.【官方双语】深度学习之反向传播算法 上/下 Part 3 ver 0.9 beta[EB/OL].https://www.bilibili.com/video/BV16x411V7Qg?p=1,2017-11-22.