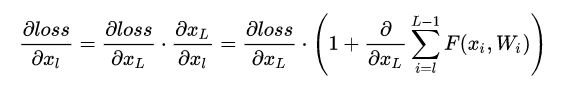神经网络参数梯度的计算方式

一、什么是梯度

· 梯度的定义

梯度是一个向量，是一个n元函数f关于n个变量的偏导数，梯度会指向各点处的函数值降低的方向。更严格的讲，梯度指示的方向是各
点处的函数值减少最多的方向。为什么这么说，因为方向导数=cos(\theta)×梯度，而\theta是方向导数的方向和梯度方向的夹角。
所以，所有的下降方向中，梯度方向下降的最多。

二、梯度法

· 什么是梯度法

深度学习中， 神经网络的主要任务是在学习时找到最优的参数（权重和偏置），这个最优参数也就是损失函数最小时的参数。但是，
一般情况下，损失函数比较复杂，参数也很多，无法确定在哪里取得最小值。所以通过梯度来寻找最小值（或者尽可能小的值）的
方法就是梯度法。

· 为什么使用梯度更新规则

在处理复杂任务上，深度网络比浅层的网络具有更好的效果。但是，目前优化神经网络的方法都是基于反向传播的思想，即根据损失
函数计算的误差通过梯度反向传播的方式，指导深度网络权值的更新优化。这样做是有一定原因的，首先，深层网络由许多非线性层
堆叠而来，每一层非线性层都可以视为是一个非线性函数 

(非线性来自于非线性激活函数），因此整个深度网络可以视为是一个复合的非线性多元函数

我们最终的目的是希望这个多元函数可以很好的完成输入到输出之间的映射，假设不同的输入，输出的最优解是 

那么，优化深度网络就是为了寻找到合适的权值，满足

取得极小值点，比如最简单的损失函数 :

,假设损失函数的数据空间是下图这样的，
我们最优的权值就是为了寻找下图中的最小值点，对于这种数学寻找最小值问题，采用梯度下降的方法再适合不过了。因此，对于神经
网络这种参数式的方法，使用梯度更新可以用来寻找最优的参数。

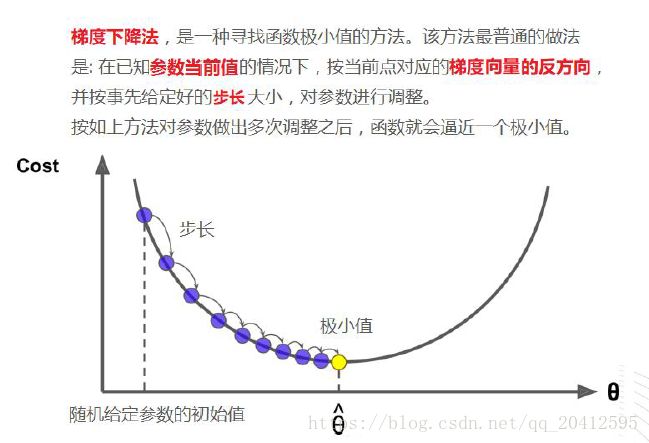
· 梯度下降

梯度下降的基本过程就和下山的场景很类似。首先，我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个
函数的最小值，也就是山底。根据之前的场景假设，最快的下山的方式就是找到当前位置最陡峭的方向，然后沿着此方向向下走，对
应到函数中，就是找到给定点的梯度 ，然后朝着梯度相反的方向，就能让函数值下降的最快！因为梯度的方向就是函数之变化最快的
方向(在后面会详细解释)，所以，我们重复利用这个方法，反复求取梯度，最后就能到达局部的最小值。

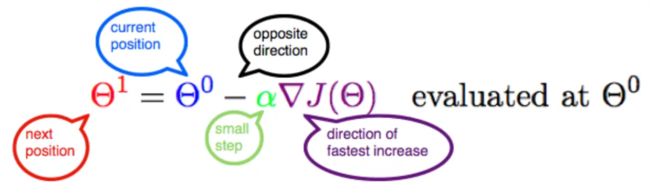
梯度下降的科学解释：

此公式的意义是：J是关于Θ的一个函数，我们当前所处的位置为Θ0点，要从这个点走到J的最小值点，也就是山底。首先我们先确定前
进的方向，也就是梯度的反向，然后走一段距离的步长，也就是α，走完这个段步长，就到达了Θ1这个点！

疑问点：
1、α是什么含义？
α在梯度下降算法中被称作为学习率或者步长，意味着我们可以通过α来控制每一步走的距离，不要走太快，步长太大会错过了最低点。
同时也要保证不要走的太慢，太小的话半天都无法收敛。所以α的选择在梯度下降法中往往是很重要的！α不能太大也不能太小，太小
的话，可能导致迟迟走不到最低点，太大的话，会导致错过最低点！
2、为什么要梯度要乘以一个负号？
梯度前加一个负号，就意味着朝着梯度相反的方向前进！我们在前文提到，梯度的方向实际就是函数在此点上升最快的方向！而我们需
要朝着下降最快的方向走，自然就是负的梯度的方向，所以此处需要加上负号。

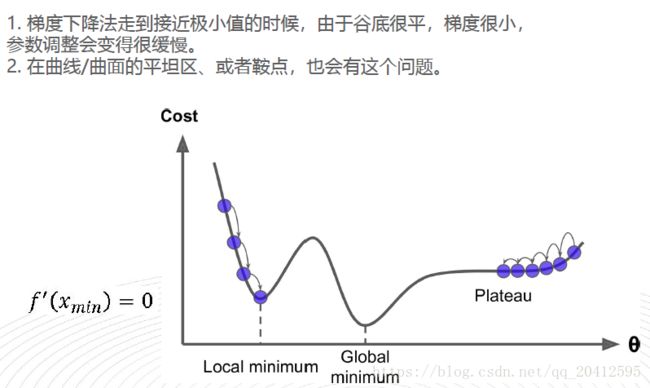
梯度下降存在的问题：
1、参数调整缓慢

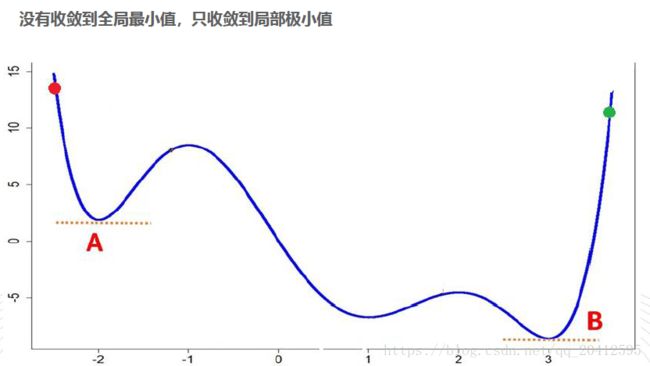
2、可能收敛于局部最小值

三、深度学习中的梯度问题

· 梯度消失与梯度爆炸

深层网络角度：在深层网络中，由于网络过深，如果初始得到的梯度过小，或者传播途中在某一层上过小，则在之后的层上得到的
梯度会越来越小，即产生了梯度消失。梯度爆炸也是同样的。不同的层学习的速度差异很大，表现为网络中靠近输出的层学习的情况很
好，靠近输入的层学习的很慢，有时甚至训练了很久，前几层的权值和刚开始随机初始化的值差不多。因此，梯度消失、爆炸，其根本
原因在于反向传播训练法则，本质在于方法问题
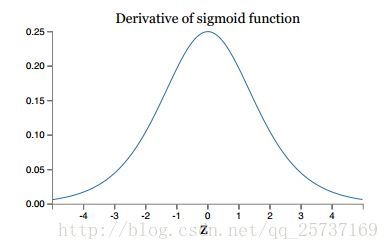
激活函数角度：计算权值更新信息的时候需要计算前层偏导信息，因此如果激活函数选择不合适，比如使用sigmoid，梯度消失就
会很明显了，原因看下图
 

左图是sigmoid的损失函数图，右边是其倒数的图像，如果使用sigmoid作为损失函数，其梯度是不可能超过0.25的，这样经过链式求
导之后，很容易发生梯度消失，sigmoid函数数学表达式为：

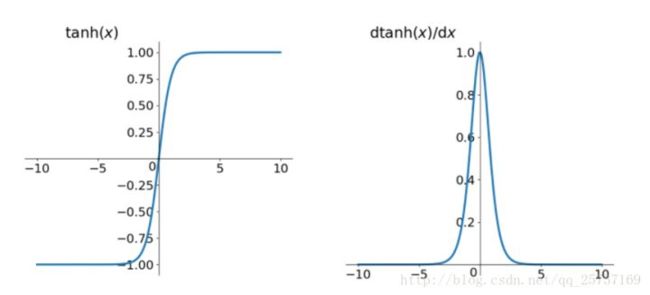
同理，tanh作为损失函数，它的导数图如下，可以看出，tanh比sigmoid要好一些，但是它的倒数仍然是小于1的。tanh数学表达为：

· 梯度消失、爆炸的解决方案

1、预训练加微调

及采取无监督逐层训练方法，其基本思想是每次训练一层隐节点，训练时将上一层隐节点的输出作为输入，而本层隐节点的输出作为下一
层隐节点的输入，此过程就是逐层“预训练”（pre-training）；在预训练完成后，再对整个网络进行“微调”（fine-tunning）。此思想
相当于是先寻找局部最优，然后整合起来寻找全局最优，此方法有一定的好处，但是目前应用的不是很多了。

2、梯度剪切与正则

梯度剪切这个方案主要是针对梯度爆炸提出的，其思想是设置一个梯度剪切阈值，然后更新梯度的时候，如果梯度超过这个阈值，那么就
将其强制限制在这个范围之内。这可以防止梯度爆炸。

权重正则化限制过拟合，如果仔细看正则项在损失函数中的形式（公式如下），其中，α 是指正则项系数，因此，如果发生梯度爆炸，
权值的范数就会变的非常大，通过正则化项，可以部分限制梯度爆炸的发生。

注：事实上，在深度神经网络中，往往是梯度消失出现的更多一些。

3、使用relu、elu、leakrelu等激活函数

激活函数讲解参考：https://blog.csdn.net/weixin_43798170/article/details/106698255

4、Batchnorm（批量归一化）

Batchnorm是深度学习发展以来提出的最重要的成果之一了，目前已经被广泛的应用到了各大网络中，具有加速网络收敛速度，提升训练稳定性
的效果，Batchnorm本质上是解决反向传播过程中的梯度问题。batchnorm全名是batch normalization，简称BN，即批规范化，通过规范化操
作将输出信号x规范化到均值为0，方差为1保证网络的稳定性。
在此只大概讲一下batchnorm为何能解决梯度问题，具体来说就是反向传播中，经过每一层的梯度会乘以该层的权重，举个简单例子： 正向传播中

，
那么反向传播中

，反向传播式子中有w的存在，所以 w 的大小影响了梯度的消失和爆炸，batchnorm就是通过对每一层的输出做
scale和shift的方法，通过一定的规范化手段，把每层神经网络任意神经元这个输入值的分布强行拉回到接近均值为0方差为1的标准正太分布，
即严重偏离的分布强制拉回比较标准的分布，这样使得激活输入值落在非线性函数对输入比较敏感的区域，这样输入的小变化就会导致损失函数
较大的变化，使得让梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。

5、构建残差结构

残差结构解读（论文：Deep Residual Learning for Image Recognition）：https://zhuanlan.zhihu.com/p/31852747

残差解决梯度问题：
首先残差单元如下

一般，残差网络中很多这样的跨层连接结构，这样的结构在反向传播中具有很大的好处，见下式：

公式第一个因子

表示损失函数到达L的梯度，小括号中的1表明短路机制可以无损地传播梯度，而另外一项残差梯度则需要经过带有weights的层，
梯度不是直接传递过来的。残差梯度不会那么巧全为-1，而且就算其比较小，有1的存在也不会导致梯度消失。所以残差